标签:指定 没有 本质 接受 必须 sub 校验 ima 部分
代数解固然不错,并且在许多运算中和几何解很接近。但是几何解,他的强大之处在于使用了比较校验。比如测试了光源是否在球外并远离球体。因为随机放置的光线经常会远离球体。
问题是为什么这两个结局方案会有如此不同。解释很简单:代数算法很没效率。把A5中的A,B,C运算和A9-A13的几何运算进行比较。可以确定以下关系:
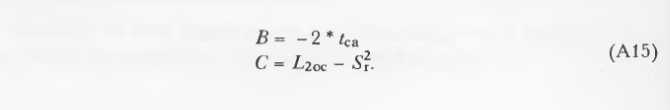
推导过程如下:
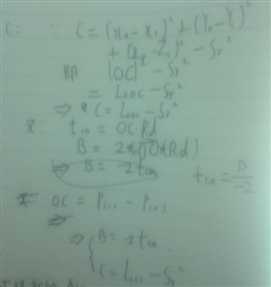
由上可得新的A14:
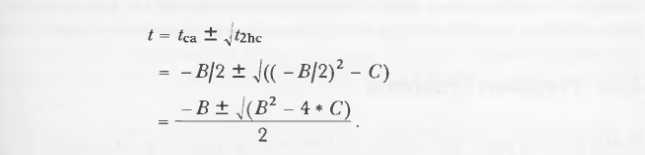
这是A6,代数解仍然比几何解复杂。因为*4和/2这种例子。回看A5:
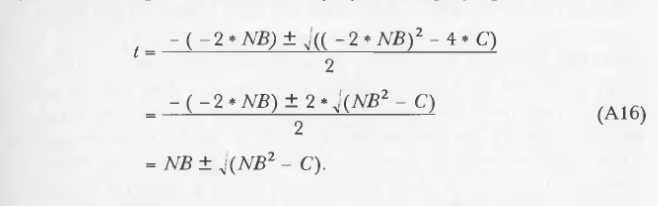
B=-2*NB NB=B/(-2)
把NB带入A5:
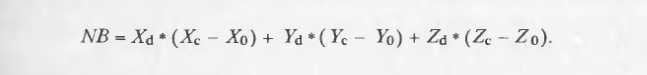
NB=tca (A10的推论)
为了消除(+-)的问题。t0,t1必须为球面计算。并在较小的正值被接受的时候。我们需要更为深入的观察。代数解的一个缺陷就是缺乏缩短处理时间的办法。在A15中,我们可以告诉光源只有C>0它才在球外。这就消除了需要计算t1,t0的状况。因为A14的标准可得知是否要从NB中添加或减去判别函数。
同样如果NB>0,射线必然远离球心。代数解最初没有很多有用的特性,通过对情况的集合分析,找到了一种更好的算法。回顾代数解。这种情况下固有的效率变得很明显。
本节要点是,研究问题的本质可以产生算法提速。代数解很简单,但他的目的是解决求线与球交点的一般问题。几何问题着眼于光线的特殊性(即光线指定了一条线的一部分)和问题的要求(即只需要最近的交点)。
标签:指定 没有 本质 接受 必须 sub 校验 ima 部分
原文地址:https://www.cnblogs.com/TooYoungTsukasa/p/9215966.html