标签:时间复杂度 blank flag 也会 val 旋转 红黑树 rand 遍历
在刷了许多道平衡树的题之后,对平衡树有了较为深入的理解,在这里和大家分享一下,希望对大家学习平衡树能有帮助。
平衡树有好多种,比如treap,splay,红黑树,STL中的set。在这里只介绍几种常用的:treap和splay(其中treap包括旋转treap和非旋转treap)。
一、treap
treap这个词是由tree和heap组合而成,意思是树上的的堆(其实就是字面意思啦qwq)。treap可以说是由二叉搜索树(BST)进化而来,二叉搜索树每个点满足它左子树中所有点权值都比它小,它右子树中所有点权值都比它大,这样二叉搜索树的中序遍历出来的序列权值就是从小到大有顺序的。对于一棵完全二叉搜索树,查询每个点的时间复杂度是O(logn)。但二叉搜索树很容易就会退化成一条链(顺序或逆序插入所有点),这样它就失去了原有的作用,于是便有了treap,treap就是在维护BST性质的同时还要维护小根堆(其实大根堆也可以)的性质——每个点的另一个权值比它所有子树上节点的都小,那么这个权值是什么呢?自然是随机数了!只有随机数才能使它成为一棵平衡树(层数在logn层左右)。那么怎么同时维护这两种数据结构的性质呢?由此就产生了旋转treap和非旋转treap(具体原理下面再讲)。
treap作为一种平衡树,既可以维护集合,也可以维护序列(splay也同样)。这两者有什么区别呢?维护集合的treap的每个点的权值(具体地说是维护BST性质的权值)是集合中每个数的具体数值,但维护序列的treap的每个点的权值是序列中每个数的下标(也就是这个数在序列中的位置),而这个数具体是什么不影响平衡树的结构,只是在求解时需要的一个数值。一般维护序列的题刚开始都会先给你一个序列,而维护集合的题每个数都是在过程中插入平衡树中的。
1、旋转treap
旋转treap维护BST和堆的性质是靠旋转实现的,旋转只有两种:左旋和右旋。如图所示。
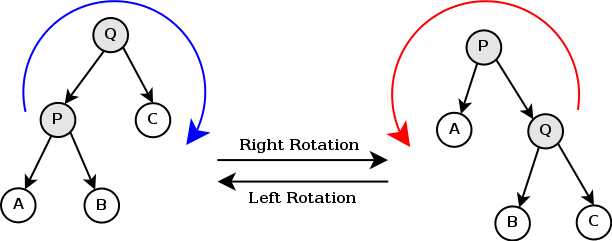
因为在插入或删除一个数时可能会在树中(而不是在叶子节点)添加或减掉一个点,所以一定会改变树的结构,也就有可能使treap的性质不满足,这时就要用旋转操作来再次恢复treap的性质。旋转treap在维护集合插入时可以把相同权值的的数放在同一个点,也可以建立不同的点来存,如何存要因题而异。
介绍旋转treap的几种常见操作(以相同权值放在同一个点为例):
变量声明:size[x],以x为根节点的子树大小;ls[x],x的左儿子;rs[x],x的右子树;r[x],x节点的随机数;v[x],x节点的权值;w[x],x节点所对应的权值的数的个数。
1)左旋和右旋
以上图为例,左旋即把Q旋到P的父节点,右旋即把P旋到Q的父节点。
以右旋为例:因为Q>B>P所以在旋转之后还要满足平衡树性质所以B要变成Q的左子树。在整个右旋过程中只改变了B的父节点,P的右节点和父节点,Q的左节点的父节点,与A,B,C的子树无关。
void rturn(int &x)
{
int t;
t=ls[x];
ls[x]=rs[t];
rs[t]=x;
size[t]=size[x];
up(x);
x=t;
}
void lturn(int &x)
{
int t;
t=rs[x];
rs[x]=ls[t];
ls[t]=x;
size[t]=size[x];
up(x);
x=t;
}
2)查询
我们以查询权值为x的点为例,从根节点开始走,判断x与根节点权值大小,如果x大就向右下查询,比较x和根右儿子大小;如果x小就向左下查询,直到查询到等于x的节点或查询到树的最底层。
3)插入
插入操作就是遵循平衡树性质插入到树中。对于要插入的点x和当前查找到的点p,判断x与p的大小关系。注意在每次向下查找时因为要保证堆的性质,所以要进行左旋或右旋。
void insert_sum(int x,int &i)
{
if(!i)
{
i=++tot;
w[i]=size[i]=1;
v[i]=x;
r[i]=rand();
return ;
}
size[i]++;
if(x==v[i])
{
w[i]++;
}
else if(x>v[i])
{
insert_sum(x,rs[i]);
if(r[rs[i]]<r[i])
{
lturn(i);
}
}
else
{
insert_sum(x,ls[i]);
if(r[ls[i]]<r[i])
{
rturn(i);
}
}
return ;
}
4)上传
每次旋转后因为子树有变化所以要修改父节点的子树大小。
void up(int x)
{
size[x]=size[rs[x]]+size[ls[x]]+w[x];
}
5)删除
删除节点的方法和堆类似,要把点旋到最下层再删,如果一个节点w不是1那就把w--就行。
void delete_sum(int x,int &i)
{
if(i==0)
{
return ;
}
if(v[i]==x)
{
if(w[i]>1)
{
w[i]--;
size[i]--;
return ;
}
if((ls[i]*rs[i])==0)
{
i=ls[i]+rs[i];
}
else if(r[ls[i]]<r[rs[i]])
{
rturn(i);
delete_sum(x,i);
}
else
{
lturn(i);
delete_sum(x,i);
}
return ;
}
size[i]--;
if(v[i]<x)
{
delete_sum(x,rs[i]);
}
else
{
delete_sum(x,ls[i]);
}
return ;
}
推荐练习题:
2、非旋转treap
非旋转treap相对于旋转treap更加简单暴力一些,只要断裂和合并两个操作就能维护树的平衡及所有操作(起码我所知的所有操作qwq),它相对于旋转treap能实现区间操作及可持久化且代码简短(对于我来说是不存在的QAQ)。
介绍一下这两个操作:
1)断裂
就是去掉一条边,把treap拆分成两棵树,对于区间操作可以进行两次断裂来分割出一段区间再进行操作。
以查找value为例,从root往下走,如果v[x]>value,那么下一步走ls[x],之后的点都比x小,把x接到右树上,下一次再接到右树上的点就是x的左儿子。
v[x]<=value与上述类似,在这里不加赘述。
void split(int x,int &lroot,int &rroot,int val)
{
if(!x)
{
lroot=rroot=0;
return ;
}
if(v[x]<=val)
{
lroot=x;
split(rs[x],rs[lroot],rroot,val);
}
else
{
rroot=x;
split(ls[x],lroot,ls[rroot],val);
}
up(x);
}
2)合并
就是把断裂开的树合并起来,因为要维护堆的性质所以按可并堆来合并。
void merge(int &x,int a,int b)
{
if(!a||!b)
{
x=a+b;
return ;
}
if(r[a]<r[b])
{
x=a;
merge(rs[x],rs[a],b);
}
else
{
x=b;
merge(ls[x],a,ls[b]);
}
up(x);
}
其他操作只要把treap断裂开,对对应区间或点进行操作再合并回去就OK了。
推荐练习题:
二、splay
splay的意思是延展树,同样满足二叉搜索树的性质,只不过splay维护平衡的方法只是旋转。每次查询会调整树的结构,使被查询频率高的条目更靠近树根。因此,就算刚开始时是一条链,在操作过程中也会变成正常的树。
splay一共有六种旋转方式,其中最基础的两种就是treap的那两种,其他四种都是由那两种演化来的。
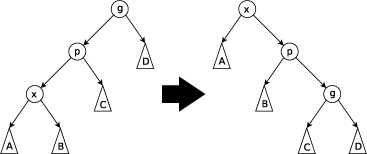
基础的旋转只能向上转一层,因此有了向上转两层的操作。但转两层自然不会那么简单,旋转是要有顺序的,以上图将x旋到g位置为例,要先将p选上去,再将x旋上去,也就是从上往下旋。
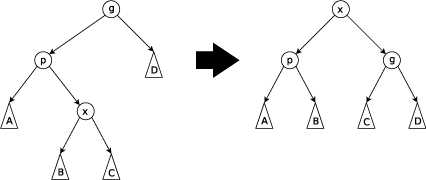
而像这种情况中将x旋到g位置,要先将x旋到p处,再旋到g处,也就是从下往上旋。
splay同样可以实现区间操作且在LCT中会用到,但splay不能可持久化。对于单点操作只需把这个点旋到根节点再查询有关信息即可,对于区间[x,y]操作,先将x-1旋到根节点,再将y+1旋到根节点的右儿子处,这样根节点右儿子的左儿子就是想要的区间。那么如何旋到根节点呢?只要两层两层往上旋就好了。
最后附上splay区间操作代码(以文艺平衡树区间翻转为例)
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int n,m;
int root;
int son[100007][3];
int size[100007];
int val[100007];
int f[100007];
int tag[100007];
int key[100007];
int sum[100007];
int d[100007];
int x,y;
int total;
int INF=1e9;
int flag=0;
bool get(int x)
{
return son[f[x]][1]==x;
}
void pushup(int x)
{
size[x]=size[son[x][0]]+size[son[x][1]]+1;
}
void pushdown(int x)
{
if(x&&tag[x])
{
tag[son[x][0]]^=1;
tag[son[x][1]]^=1;
swap(son[x][0],son[x][1]);
tag[x]=0;
}
}
void rotate(int x)
{
int fa=f[x];
int anc=f[fa];
int k=get(x);
pushdown(fa);
pushdown(x);
son[fa][k]=son[x][k^1];
f[son[fa][k]]=fa;
son[x][k^1]=fa;
f[fa]=x;
f[x]=anc;
if(anc)
{
son[anc][son[anc][1]==fa]=x;
}
pushup(fa);
pushup(x);
}
void splay(int x,int goal)
{
for(int fa;(fa=f[x])!=goal;rotate(x))
{
if(f[fa]!=goal)
{
rotate((get(fa)==get(x))?fa:x);
}
}
if(!goal)
{
root=x;
}
}
int build(int fa,int l,int r)
{
if(l>r)
{
return 0;
}
int mid=(l+r)>>1;
int now=++total;
key[now]=d[mid];
f[now]=fa;
tag[now]=0;
son[now][0]=build(now,l,mid-1);
son[now][1]=build(now,mid+1,r);
pushup(now);
return now;
}
int rank(int x)
{
int now=root;
while(1)
{
pushdown(now);
if(x<=size[son[now][0]])
{
now=son[now][0];
}
else
{
x-=size[son[now][0]]+1;
if(!x)
{
return now;
}
now=son[now][1];
}
}
}
void turn(int l,int r)
{
l=rank(l);
r=rank(r+2);
splay(l,0);
splay(r,l);
pushdown(root);
tag[son[son[root][1]][0]]^=1;
}
void write(int now)
{
pushdown(now);
if(son[now][0])
{
write(son[now][0]);
}
if(key[now]!=-INF&&key[now]!=INF)
{
if(flag==0)
{
printf("%d",key[now]);
flag=1;
}
else
{
printf(" %d",key[now]);
}
}
if(key[son[now][1]])
{
write(son[now][1]);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
d[i+1]=i;
}
d[1]=-INF;
d[n+2]=INF;
root=build(0,1,n+2);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
turn(x,y);
}
write(root);
return 0;
}
标签:时间复杂度 blank flag 也会 val 旋转 红黑树 rand 遍历
原文地址:https://www.cnblogs.com/Khada-Jhin/p/9215468.html