标签:als display ring enter for .com etc 观察 变量
从数学上讲,卷积与加减乘除一样是一种运算,其运算的根本操作是将两个函数的其中一个先平移,然后再与另一个函数相称后的累加和。这个运算过程中,因为涉及到积分、级数的操作,所以看起来很复杂。在卷积(转自wiki百科)中已经讲过了卷积的定义如下所示:
对于定义在连续域的函数,卷积定义为

对于定义在离散域的函数,卷积定义为
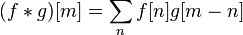
这里令U(x,y) = f(x)g(y) ,考虑到函数 f 和 g 应该地位平等,即变量 x 和 y 应该地位平等,一种可取的办法就是沿直线 x+y = t将U(x,y)卷起来。下面为t取实际值的时候的坐标图,可以看到不同取值的t可以遍历整个平面。
将x+y=t中t取一次定值(这个定值可能是我们想要知道的某时刻的结果或着某种特征,由我们赋值),代入到U(x,y)中,就相当于U(x,y)所在平面沿着x+y=t直线做一次旋转如下列动图所示:

这里便是完成了整个卷积的降维过程,完成降维过程后,U(x,y)也就从一个二元函数 U(x,y) = f(x)g(y) 被卷成一元函数 V(x)=f(x)g(t-x),最后再对x求积分(即遍历降维后的轴上的特征点之和)。
编写卷积的程序,需要根据其离散方程组来进行了解。前面已经知道了卷积的离散函数的定义公式为:
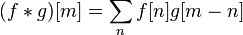
在用C语言等其他语言进行实现是可以采用定义,利用两个for循环完成代码。
根据离散公式,可以编写如下C++代码:
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
using namespace std;
float min(float a, float b)
{
return a < b ? a : b;
}
void convolution(float *input1, float *input2, float *output, int mm, int nn)
{
float *xx = new float[mm + nn - 1];
float *tempinput2 = new float[mm + nn - 1];
for (int i = 0; i < nn; i++)
{
tempinput2[i] = input2[i];
}
for (int i = nn; i < mm + nn - 1; i++)
{
tempinput2[i] = 0.0;
}
// do convolution
for (int i = 0; i < mm + nn - 1; i++)
{
xx[i] = 0.0;
int tem = (min(i, mm)) == mm ? mm - 1 : min(i, mm);
for (int j = 0; j <= tem; j++)
{
xx[i] += (input1[j] * tempinput2[i - j]);
}
}
// set value to the output array
for (int i = 0; i < mm + nn - 1; i++)
output[i] = xx[i];
delete[] xx;
}
int main()
{
float a[3] = {2,6,4 };
float b[5] = {1,2,5,4,8};
float *c = new float[9];
convolution(a, b, c, 3, 5);
for (int i = 0; i < 7; i++)
{
cout << c[i] << " ";
}
getchar();
return 0;
}
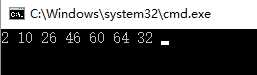
运行结果如上图所示,打开matlab进行验证有:
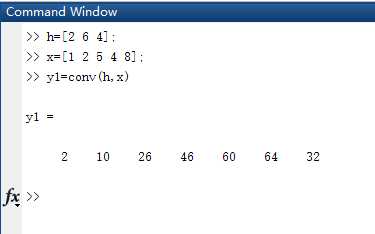
卷积的列表法计算 :
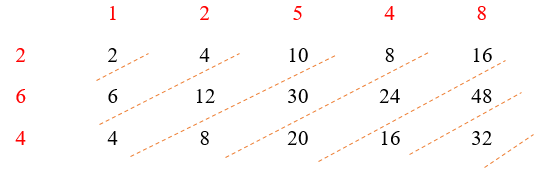
如图所示:斜线上数据相加,便是卷积结果;该方法适合用于并行计算求卷积。
打个比方,往平静的水面里面扔石头。我们把水面的反应看作是一种冲击响应。水面在t=0时刻石头丢进去的时候会激起高度为h(0)的波纹,但水面不会立马归于平静,随着时间的流逝,波纹幅度会越来越小,在t=1时刻,幅度衰减为h(1), 在t=2时刻,幅度衰减为h(2)……直到一段时间后,水面重复归于平静。
从时间轴上来看,我们只在t=0时刻丢了一块石头,其它时刻并没有做任何事,但在t=1,2….时刻,水面是不平静的,这是因为过去(t=0时刻)的作用一直持续到了现在。
那么,问题来了:
如果我们在t=1时刻也丢入一块石子呢?此时t=0时刻的影响还没有消失(水面还没有恢复平静)新的石子又丢进来了,那么现在激起的波浪有多高呢?答案是当前激起的波浪与t=0时刻残余的影响的叠加。那么t=0时刻对t=1时刻的残余影响有多大呢?
为了便于说明,接下来我们作一下两个假设:
1. 水面对于“单位石块”的响应是固定的
2. 丢一个两倍于的“单位石块”的石块激起的波纹高度是丢一个石块的两倍(即系统满足线性叠加原理)
现在我们来计算每一时刻的波浪有多高:
y(0)=x(0)*h(0);
当前石块引起的影响x(1)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(1);
y(1)=x(1)*h(0)+ x(0)*h(1);
当前石块引起的影响x(2)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(2);
t=1时刻石块x(1)引起的残余影响x(1)*h(1);
y(2)=x(2)*h(0)+ x(1)*h(1)+x(0)*h(2);
……
当前石块引起的影响x(N)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(N);
t=1时刻石块x(1)引起的残余影响x(1)*h(N-1);
y(N)=x(N)*h(0)+ x(N-1)*h(1)+x(N-2)*h(2)+…+x(0)*h(N);
这就是离散卷积的公式了
理解了上面的问题,下面我们来看看“翻转”是怎么回事:
当我们每次要丢石子时,站在当前的时间点,系统的对我们的回应都是h(0),时间轴之后的(h(1),h(2).....)都是对未来的影响。而整体的回应要加上过去对于现在的残余影响。
现在我们来观察t=4这个时刻。
站在t=0时刻看他对于未来(t=4)时刻(从现在往后4秒)的影响,可见是x(0)*h(4)
站在t=1时刻看他对于未来(t=4)时刻的影响(从现在往后3秒),可见是x(1)*h(3)
站在t=2时刻看他对于未来(t=4)时刻的影响(从现在往后2秒),可见是x(2)*h(2)
站在t=3时刻看他对于未来(t=4)时刻的影响(从现在往后1秒),可见是x(3)*h(1)
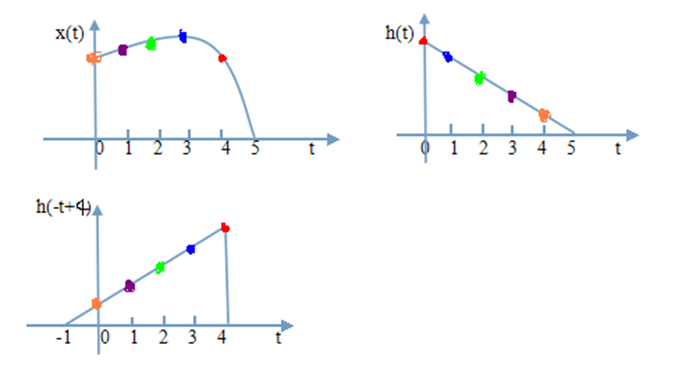
所以所谓的翻转只是因为你站立的现在是过去的未来,而因为h(t)始终不变,故h(1)其实是前一秒的h(1),而前一秒的h(1)就是现在,所以从当前x(4)的角度往左看,你看到的是过去的作用。h(t)未翻转前,当从h(0)往右看,你看到的是现在对于未来的影响,当翻转h(t)之后,从h(0)往左看,你依次看到的越来越远的过去对现在的影响,而这个影响,与从x=4向左看的作用影响相对应(都是越来越远的过去),作用与作用的响应就对应起来了,这一切的本质,是因为你站立的时间观察点和方向在变。
标签:als display ring enter for .com etc 观察 变量
原文地址:https://www.cnblogs.com/noticeable/p/9226203.html