标签:ack ace complete 二叉树 order else logs 代码 avl
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
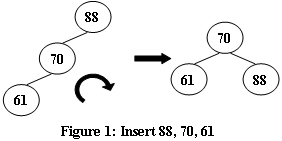 | 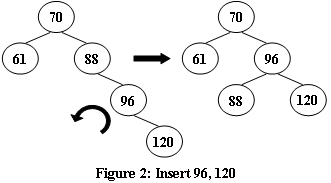 |
|---|---|
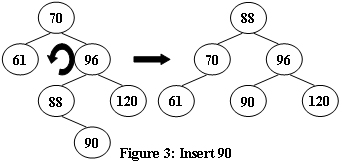 |
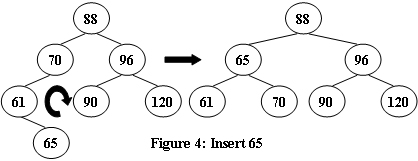 |
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.
Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.
5
88 70 61 63 65
70 63 88 61 65
YES
8
88 70 61 96 120 90 65 68
88 65 96 61 70 90 120 68 NO
题目大意:构建一颗avl,并且判断是否是完全二叉树, 输出层序遍历;
尝试用了算法笔记上面的方法, 代码的思路更加清晰一些, 构造的时间比以前的方法短一些;
区别在于,在节点中添加了记录节点高度的变量, 在求节点高度的时候,不用递归的去求高度
引用传值,也让代码简洁很多;
在左旋右旋的过程中跟新节点高度;
如何证明二叉树是完全二叉树的方法见:https://www.cnblogs.com/mr-stn/p/9232618.html
注意点:在c++中0被认作是false,其他的值认为是true;
1 #include<iostream> 2 #include<vector> 3 #include<queue> 4 #include<algorithm> 5 using namespace std; 6 struct node{ 7 int val, height; 8 node *left, *right; 9 }; 10 11 int max(int a, int b){ 12 if(a>b) return a; 13 else return b; 14 } 15 int getHeight(node* root){ 16 if(root==NULL) return 0; 17 return root->height; 18 } 19 20 21 void updateHeight(node* &root){ 22 root->height = max(getHeight(root->left) , getHeight(root->right)) + 1; 23 } 24 25 void leftRoate(node* &root){ 26 node* temp=root->right; 27 root->right=temp->left; 28 temp->left=root; 29 updateHeight(root); 30 updateHeight(temp); 31 root = temp; 32 } 33 34 void rightRoate(node* &root){ 35 node* temp=root->left; 36 root->left = temp->right; 37 temp->right=root; 38 updateHeight(root); 39 updateHeight(temp); 40 root = temp; 41 } 42 43 44 int getBalanceFactor(node* root){ 45 return getHeight(root->left) - getHeight(root->right); 46 } 47 48 49 void insert(node* &root, int val){ 50 if(root==NULL){ 51 root = new node; 52 root->height=1; 53 root->val = val; 54 root->left = root->right=NULL; 55 return ; 56 }else if(root->val > val){ 57 insert(root->left, val); 58 updateHeight(root); 59 if(getBalanceFactor(root)==2){ 60 if(getBalanceFactor(root->left)==1) rightRoate(root); 61 else{ 62 leftRoate(root->left); 63 rightRoate(root); 64 } 65 } 66 }else{ 67 insert(root->right, val); 68 updateHeight(root); 69 if(getBalanceFactor(root)==-2){ 70 if(getBalanceFactor(root->right)==-1) leftRoate(root); 71 else{ 72 rightRoate(root->right); 73 leftRoate(root); 74 } 75 } 76 } 77 } 78 79 int main(){ 80 int n, i; 81 cin>>n; 82 vector<int> v(n); 83 for(i=0; i<n; i++) scanf("%d", &v[i]); 84 node *root=NULL; 85 for(i=0; i<n; i++) insert(root, v[i]); 86 queue<node*> q; 87 q.push(root); 88 int flag=0, f=0; 89 vector<int> ans; 90 while(q.size()){ 91 node* temp=q.front(); 92 q.pop(); 93 if(temp) ans.push_back(temp->val); 94 if(temp->left != NULL){ 95 q.push(temp->left); 96 if(flag) f=1; 97 }else flag=true; 98 if(temp->right != NULL){ 99 q.push(temp->right); 100 if(flag) f=1; 101 }else flag=true; 102 } 103 cout<<ans[0]; 104 for(i=1; i<ans.size(); i++) cout<<" "<<ans[i]; 105 if(f) cout<<endl<<"NO"; 106 else cout<<endl<<"YES"; 107 return 0; 108 }
PAT 1123 Is It a Complete AVL Tree
标签:ack ace complete 二叉树 order else logs 代码 avl
原文地址:https://www.cnblogs.com/mr-stn/p/9233399.html