约束优化方法

标签：图片   bsp   集合   可行性   技术分享   联系   分享图片   .com   形式   

一般形式的约束优化问题是：

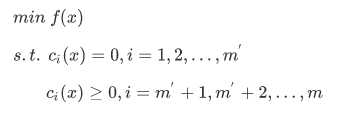
有以下相关概念：

1. 可行域——满足约束条件的x的集合

2.x点的有效约束——在x点等号成立的约束

3.可行方向

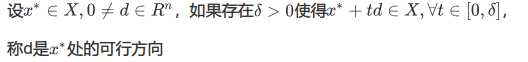
在x*处的可行方向的集合记为FD(x*,X)

4.线性化可行方向

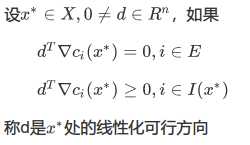
在x*处的线性化可行方向的集合记为LFD(x*,X)

5.序列可行方向

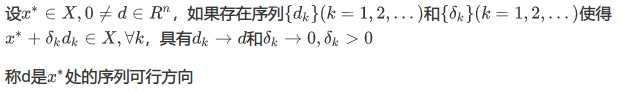
在x*处的线序列可行方向的集合记为SFD(x*,X)

几个约束规范条件：

1.约束规范条件（CQ）：LFD(x*,X)=SFD(x*,X)

2.线性函数约束规范条件（LFCQ）：所有的约束函数都是线性函数

3.线性无关约束规范条件（LICQ）：约束函数的梯度线性无关

 可以证明：线性函数约束规范条件或线性无关约束规范条件成立，则约束规范条件成立

约束优化的一阶最优条件称为kkt条件：

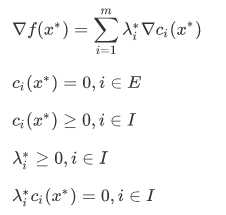
kkt条件从上到下依次称为：驻点条件、可行性条件、可行性条件、乘子非负条件、互补松弛条件

相应的，有kkt定理：如果约束规范条件满足，则存在λ_i^*(i=1,2,...,m)，使得kkt条件成立

与kkt条件有密切联系的一个函数是Lagrange函数：

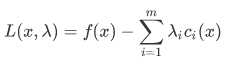
关于约束优化问题，还有几个一阶和二阶最有条件：

首先定义LFD的子集F₂：

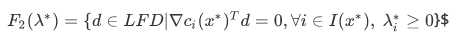
一阶最优性充分条件：

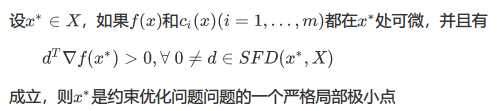
二阶最优性必要条件：

二阶最优性充分条件：

约束优化方法

标签：图片   bsp   集合   可行性   技术分享   联系   分享图片   .com   形式   

原文地址：https://www.cnblogs.com/kisetsu/p/9233334.html