标签:迭代 oss function sklearn 颜色表 预处理 增加 rom 颜色
什么是过拟合?
在训练假设函数模型h时,为了让假设函数总能很好的拟合样本特征对应的真实值y,从而使得我们所训练的假设函数缺乏泛化到新数据样本能力。
过拟合会在变量过多同时过少的训练时发生,我们有两个选择,一是减少特征的数量,二是正则化,今天我们来重点来讨论正则化,它通过设置惩罚项让参数θ足够小,要让我们的代价函数足够小,就要让θ足够小,由于θ是特征项前面的系数,这样就使特征项趋近于零。岭回归与Lasso就是通过在代价函数后增加正则化项。
多元线性回归损失函数:

岭回归回归代价函数:
我们从矩阵的角度来看。机器学习的核心在在于求解出θ使J(θ)最小。怎样找到这个θ,经典的做法是使用梯度下降通过多次迭代收敛到全局最小值,我们也可以用标准方程法直接一次性求解θ的最优值。当回归变量X不是列满秩时, XX‘的行列式接近于0,即接近于奇异,也就是某些列之间的线性相关性比较大时,传统的最小二乘法就缺乏稳定性,模型的可解释性降低。因此,为了解决这个问题,需要正则化删除一些相关性较强特征。
标准方程法:
加上正则化后:
这里,λ>=0是控制收缩量的复杂度参数:λ的值越大,收缩量越大,共线性的影响越来越小。在不断增大惩罚函数系数的过程中,画出估计参数0(λ)的变化情况,即为岭迹。通过岭迹的形状来判断我们是否要剔除掉该特征(例如:岭迹波动很大,说明该变量参数有共线性)。
步骤:1.首先要对数据进行一些预处理,尽量把保持所有特征在一个范围内,使用特征缩放和均值归一化来处理特征值是很有必要的,否则,不同特征的特征值大小是没有比较性的。
2.其次构建惩罚函数,针对不同的λ,画出岭迹图。
3.根据岭迹图,选择要剔除那些特征。
将岭系数绘制为正则化的函数
本例显示了共线性对估计量系数的影响。岭回归是本例中使用的估计量。 每种颜色表示系数矢量的不同特征,并且这是作为正则化参数的函数显示的。这个例子还显示了将岭回归应用于高度病态的基质的有用性。对于这样的矩阵,目标变量的轻微变化会导致计算权重的巨大差异。在这种情况下,设置一定的正则化(λ)来减少这种变化(噪音)是有用的。当λ很大时,正则化效应支配平方损失函数,并且系数趋于零。在路径的末尾,由于λ趋于零,并且解决方案倾向于普通最小二乘,所以系数显示出大的振荡。 在实践中,需要调整λ以使两者之间保持平衡。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
#X为一个10*10的矩阵
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
##############################################################################
#设置不同的lambda和参数
n_lambda = 200
lambda = np.logspace(-10, -2, n_lambda)
coefs = []
for a in lambda:
ridge = linear_model.Ridge(lambda=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_)
# #############################################################################
#显示绘制结果
ax = plt.gca()
ax.plot(lambda, coefs)
ax.set_xscale(‘log‘)
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel(r‘$\lambda$‘)
plt.ylabel(‘weights‘)
plt.title(‘Ridge coefficients as a function of the regularization‘)
plt.axis(‘tight‘)
plt.show()结果: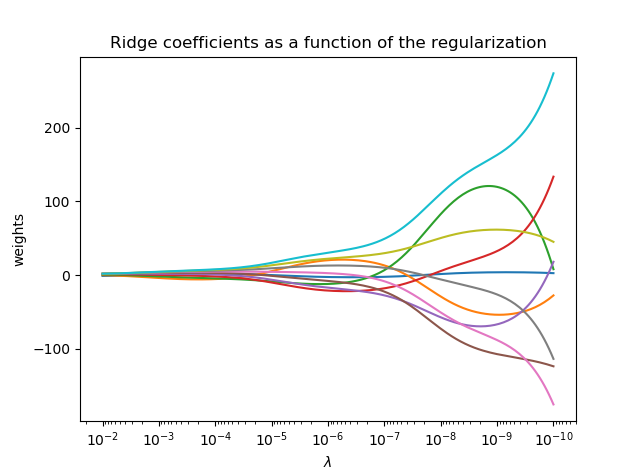
感谢您的阅读,如果您喜欢我的文章,欢迎关注我哦

标签:迭代 oss function sklearn 颜色表 预处理 增加 rom 颜色
原文地址:http://blog.51cto.com/13820241/2133425