标签:git += 编写 sig 线性 .com info 分享图片 代码
ARMA模型属于信号现代谱估计的范畴,AR模型常用于信号的线性预测。AR模型最后归结为线性方程,MA最后为非线性方程,因此,AR模型使用较多。
AR模型最后归结为解Yule-Walker方程,对应矩阵为Toeplitz矩阵,存在Levinson快速算法,这将在后面介绍,这里介绍使用C编写的ARMA模型程序。
一、公式简介
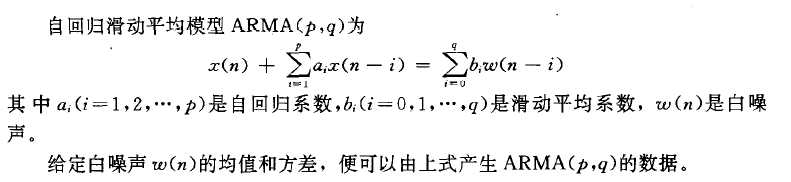
/*****************************************
**********ARMA(p,q)***********************
a:自回归系数
b:滑动平均系数
p:自回归阶数
q:滑动平均阶数
mean:gauss白均值
sigma:gauss白方差
seed:随机数种子
x:存放ARMA(p,q)产生的数据
n:ARMA(p,q)产生的数据长度
******************************************/
void arma(const double* a,const double* b,int p,int q,double mean,double sigma,long int* seed,double* x,int n)
{
int i,k,m;
double s,*w;
w = (double*)malloc(n * sizeof(double));
for(k=0;k<n;k++)
w[k] = gauss(mean,sigma,seed);
x[0] = b[0] * w[0];
for(k=1;k<=p;k++)
{
s = 0.0;
for(i=1;i<=k;i++)
s += a[i] * x[k-i];
s = b[0] * w[k] - s;
if(0 == q)
{
x[k] = s;
continue;
}
m = (k > q) ? q : k;
for(i=1;i<=m;i++)
s += b[i] * w[k-i];
x[k] = s;
}
for(k = (p+1);k<n;k++)
{
s = 0.0;
for(i=1;i<=p;i++)
s += a[i] * x[k-i];
s = b[0] * w[k] - s;
if(0 == q)
{
x[k] = s;
continue;
}
for(i=1;i<=q;i++)
s += b[i] * w[k-i];
x[k] = s;
}
free(w);
}
完整代码参考:https://github.com/HeYingnan/dsp
标签:git += 编写 sig 线性 .com info 分享图片 代码
原文地址:https://www.cnblogs.com/ziphe-from-teacher-chen/p/9236489.html