PAT 乙级 1049 数列的片段和

标签：map   解法   ble   ++   规律   string   set   5.0   乙级   

输入样例：
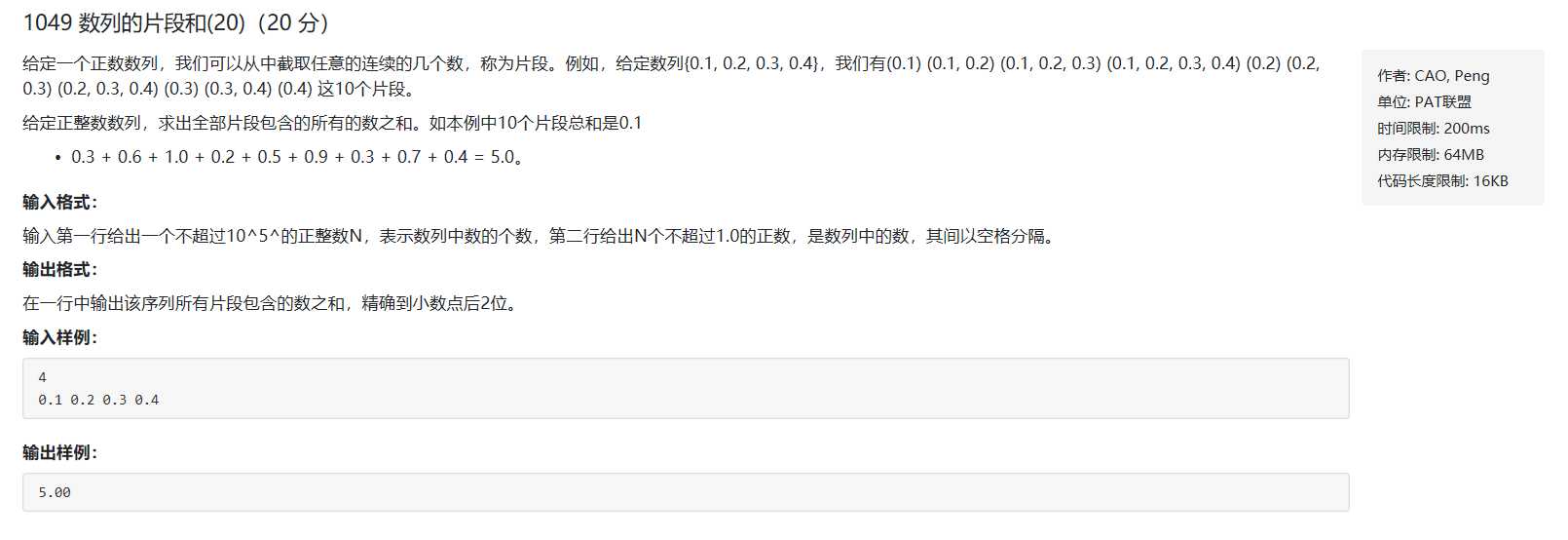
4
0.1 0.2 0.3 0.4
输出样例：
5.00

暴力解法时间复杂度Θ(n^3) 空间复杂度Θ(n) 这种复杂度肯定会超时的。

一开始我还以为是DP，优化掉了一层循环时间复杂度Θ(n^2) 空间复杂度Θ(n) 结果还是超时了。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <stack>
#include <algorithm>

using namespace std;

double sum(double* p, int n);

int main()
{
    int n;
    cin >> n;
    double* p = new double[n];
    for (int i = 0; i<n; i++)
        scanf("%lf", &p[i]);
    printf("%.2lf", sum(p, n));
    delete p;
    return 0;
}

double sum(double* p, int n)
{
    double* q = new double[n];
    bool* r = new bool[n];
    memset(q, 0, n * sizeof(double));
    memset(r, 0, n * sizeof(bool));
    double sum = 0;
    double allSum = 0;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j + i <= n; j++)
        {
            q[j] = q[j] + p[j + i - 1];
            sum += q[j];
        }
    }
    delete q, r;
    return sum;
}

最后我才发现这是一道数学题，需要找一下规律：

给定5个数 0.1 0.2 0.3 0.4 0.5，出现下列连续子列

[0.1] [0.1 0.2] [0.1 0.2 0.3] [0.1 0.2 0.3 0.4] [0.1 0.2 0.3 0.4 0.5]

[0.2] [0.2 0.3] [0.2 0.3 0.4] [0.2 0.3 0.4 0.5]

[0.3] [0.3 0.4] [0.3 0.4 0.5]

[0.4] [0.4 0.5]

[0.5]

0.1的出现次数为 5 ，5 × 1 = 5。
0.2的出现次数为 8 ，4 × 2 = 8。
0.3的出现次数为 9 ，3 × 3 = 9。
0.4的出现次数为 8 ，2 × 4 = 8。
0.5的出现次数为 5 ，1 × 5 = 5。

可以发现规律某个数字在序列中的出现次数为 (n-i) × (i+1) ,n为原始序列长度i为当前序列所处的位置（从0开始计算）。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <stack>
#include <algorithm>

using namespace std;

double sum(double* p, int n);

int main()
{
    int n;
    cin >> n;
    double* p = new double[n];
    for (int i = 0; i<n; i++)
        scanf("%lf", &p[i]);
    printf("%.2lf", sum(p, n));
    return 0;
}

double sum(double* p, int n)
{
  double sum=0;
  for(int i=0;i<n;i++)
  {
    sum+=p[i]*(n-i)*(i+1);
  }
  return sum;
}

PAT 乙级 1049 数列的片段和

标签：map   解法   ble   ++   规律   string   set   5.0   乙级   

原文地址：https://www.cnblogs.com/FDProcess/p/9245873.html