标签:cti 动态 变量 element 推导 idt alt spl 分享
本文是对参考1论文中模型的详细推导,以供计算机分析之用。
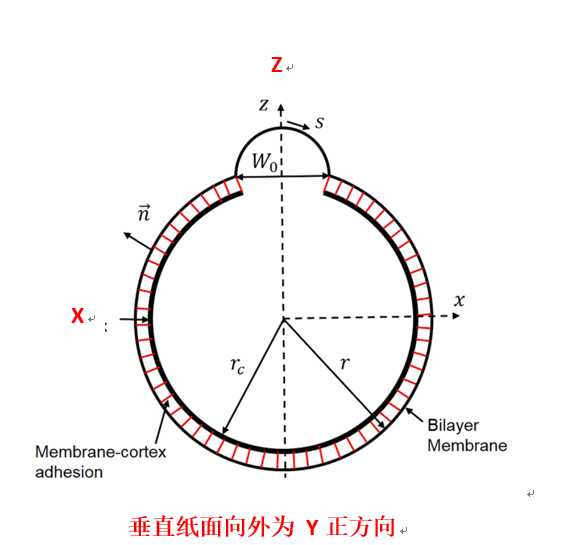
图1 细胞受力在y向投影
蠕动流
细胞液和细胞质可以视为蠕动流体,在流动过程中其黏性力远大于惯性力,
蠕动流的控制方程(斯托克斯方程)
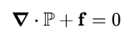
其中双线P为 柯西应力张量,也可表示为σij,包含黏性力与压力,f则为体积力(可视为内部应力)。
详见 https://zh.wikipedia.org/wiki/%E6%96%AF%E6%89%98%E5%85%8B%E6%96%AF%E6%B5%81
因为细胞液不可压缩,视为牛顿流体,斯托克斯方程变为(3维向量形式)
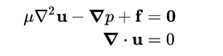
u是流体的速度, p是压力的梯度, μ是动态粘度,f是体积力。
详见 https://en.wikipedia.org/wiki/Stokes_flow
结合图1,只看y向投影,则有
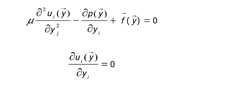
即为论文中公式1
为了求解式2,加入边界条件,变为
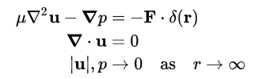
其中 为3维狄拉克函数, 表示只在原点处有力,即力是位于原点的点力。力场梯度在无穷远处为0.
方程的解为
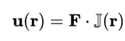
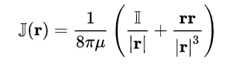
双线J为力的张量场, 双线I为单位张量,r为过原点的任意矢量。
对于连续场(细胞模型)式4可以写成积分形式
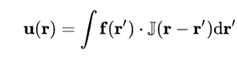
f为力场密度,r’为过原点的任意矢量
式6为三维向量形式,可将其投影在y面上,降为面积分
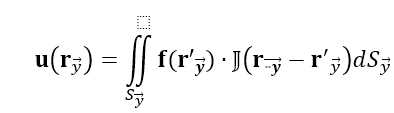
对于弹性体(细胞膜)来说,应力和形变的关系可以用下面公式表达
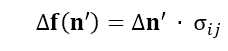
其中, 为力密度, 为体变量, 为弹性系数张量
投影到y面,则有
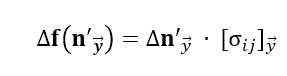
结合式7,则有
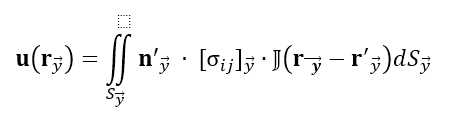
令
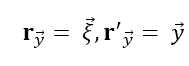
则有
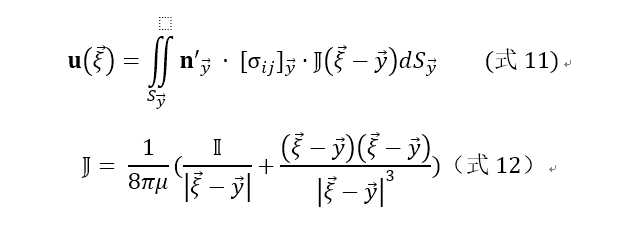
等同于论文式4和式5
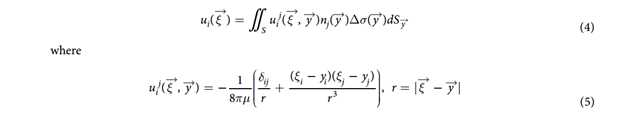
参考资料:《A combined experimental and theoretical investigation on cellular blebbing》
《Cell membrane wrapping of a spherical thin elastic》
《INTERACTION BETWEEN BENDING AND TENSION FORCES IN BILAYER MEMBRANES》
《The Boundary Element Method in Fluid》
《Theoretical Model for Cellular Blebbing》
标签:cti 动态 变量 element 推导 idt alt spl 分享
原文地址:https://www.cnblogs.com/qiantuo1234/p/9246389.html