标签:内存 优化 数组 分组 存储结构 比较 无向图 复杂 要求
由于图的结构比较复杂,任意两个顶点之间都可能存在联系,因此无法以数据元素在内存中的物理位置来表示元素之间的关系,也就是说,图不可能用简单的顺序存储结构来表示。
多重链表的方式,即以一个数据域和多个指针域组成的结点表示图中的一个结点,尽管可以实现图结构,但是如果各个顶点的度数相差很大,按度数最大的顶点设计结点结构会造成很多存储单元的浪费,而若按每个顶点自己的度数设计不同的结点结构,又带来操作的不变。
图的类型主要有4种:无向图、有向图、无向网和有向网。
图的五种常见的存储结构:领接矩阵、领接表、十字链表、领接多重表和边集数组。
一、领接矩阵
图的领接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一位数组存储图中顶点信息,一个二维数组(称为领接矩阵)存储图中的边或弧的信息。
1.举例
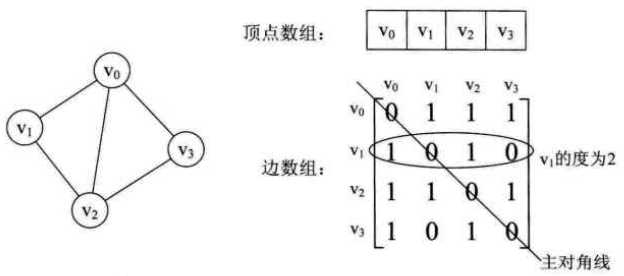
无向图的领接矩阵的第i行或第i列的非零元素个数正好是第i个顶点的度。
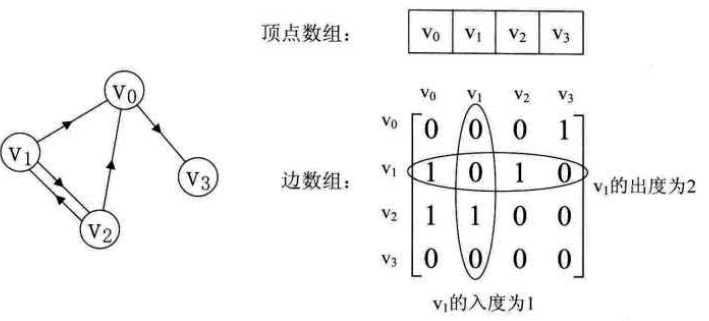
有向图的领接矩阵的第i行的非零元素个数正好是第i个顶点的出度,第i列的非零元素个数正好是第i个顶点的入度。
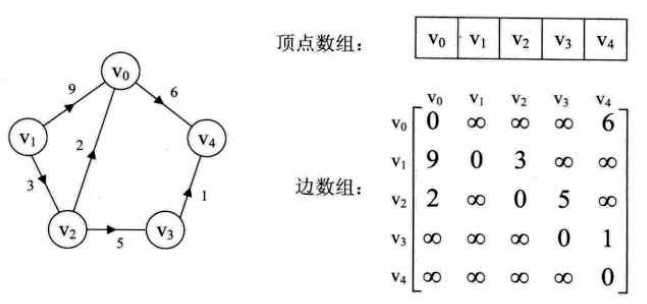
二、邻接表
对于边数相对顶点较少的图,领接矩阵存在对存储空间的极大浪费的。可以考虑对边或弧使用链式存储的方式来避免空间浪费的问题。
领接表是由两部分组成。顶点用一个一维数组存储。而每个顶点的所有领接点构成一个线性表,由于领接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
对于有n个顶点和e条边的无向图,其邻接表有n个顶点结点和2e个边结点,而对于有n个顶点和e条弧的有向图,其邻接表有n个顶点结点和e个弧结点。显然,对于稀疏图,邻接表比邻接矩阵节省存储空间。
1.举例说明
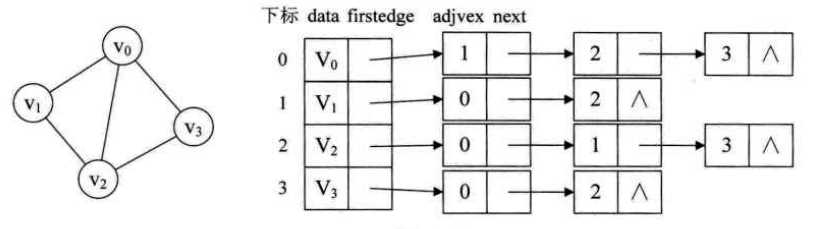
无向图的邻接表中,顶点vi的度恰好等于该顶点的领接表中边结点的个数
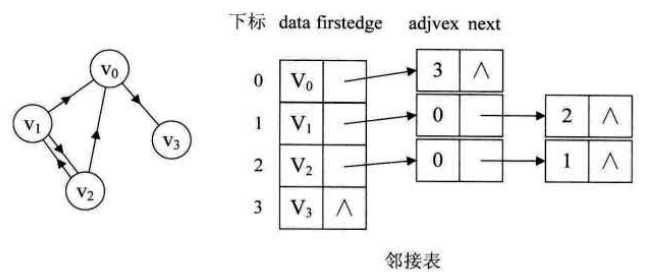
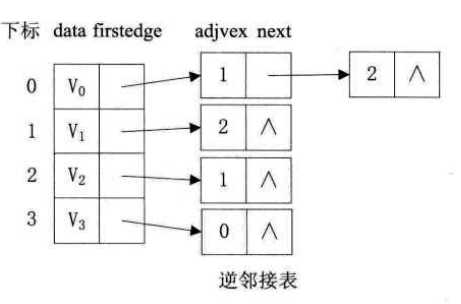
有向图中,顶点vi的领接表中边结点的个数仅为该顶点的出度,若要求顶点的入度,则需遍历整个邻接表。有时为了便于求有向图中顶点的入度,可以通过建立一个有向图的逆邻接表得到。逆邻接表就是对图中的每个顶点vi建立一个链接以vi为重点的弧的边表。
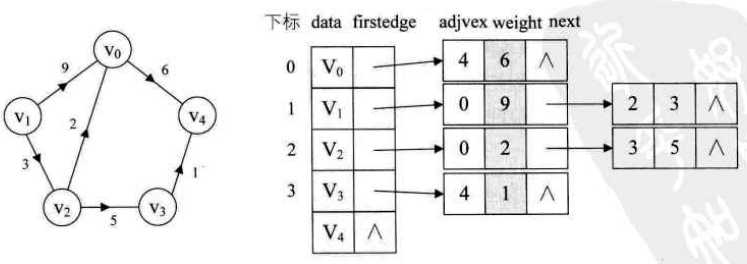
三、十字链表
对于有向图来说,邻接表是有缺陷的。关心了入度问题,想了解入度就必须要遍历整个图才能知道,反之,逆领接表解决了入度却不了解出度的情况。而十字链表可以把它们整合在一起。
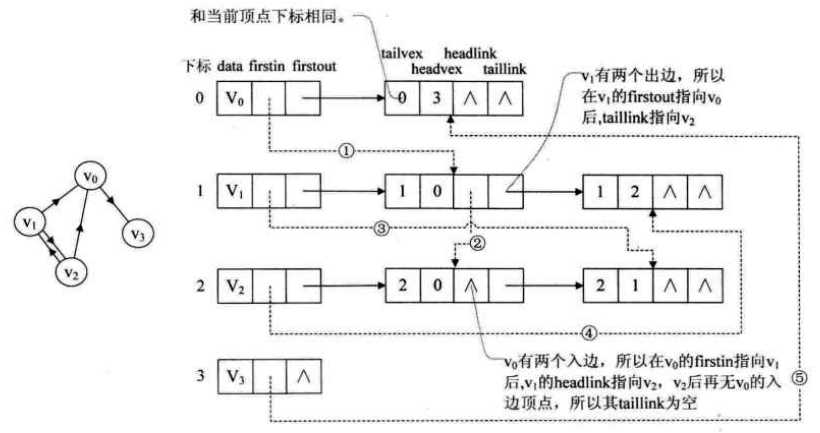
十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以vi为尾的弧,也容易找到以vi为头的弧,因而容易求得顶点的出度和入度。而且,除了结构复杂一点外,创建图算法的时间复杂度和邻接表相同,因此,在有向图的应用中,十字链表是非常好的数据结构模型。
四、领接多重表
有向图的优化存储可以用十字链表来解决,对于无向图来说,如果更关注边的操作,可以仿照十字链表的方式,对边表结点的结构进行一些改造,即形成邻接多重表。
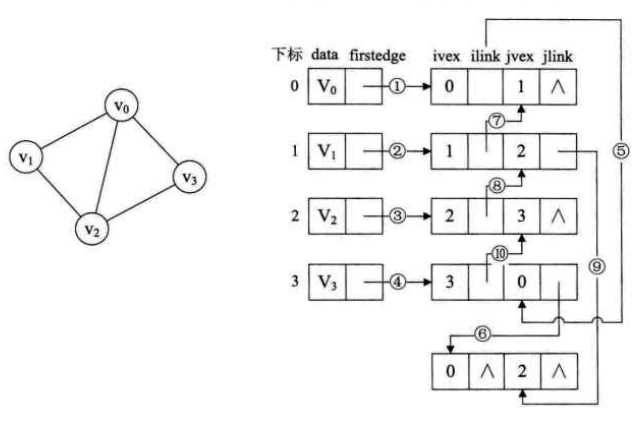
邻接多重表与邻接表的区别,仅仅是在于同一条边在邻接表中用两个结点表示,而在邻接多重表中只有一个结点。这样对边的操作就方便多了。
五、边集数组
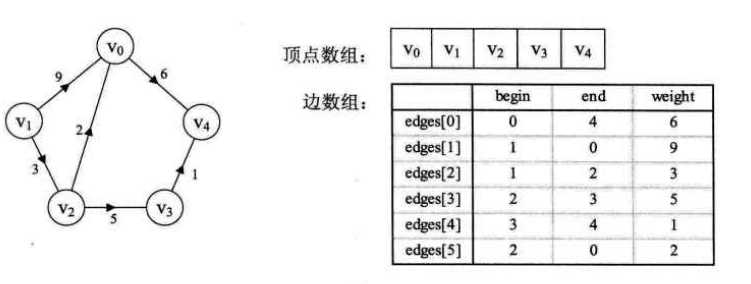
边集数组是由两个一位数组构成。一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标、终点下标和权组成。显然边集数组关注的是边的集合,在边集数组中要查找一个顶点的度需要扫描整个边数组,效率并不高。因此它更适合对边依次进行处理的操作,而不适合对顶点的相关的操作。
标签:内存 优化 数组 分组 存储结构 比较 无向图 复杂 要求
原文地址:https://www.cnblogs.com/BigJunOba/p/9247682.html