标签:src 顶点 ber can 自己 ali tps load class
完蛋了要挂科了,赶紧更新个专题冷静一下
PS.仅按A题人数顺序更新,选择性忽略部分题
PPS.这个专题应该比较休闲吧
给定初始n和目标m,存在两种操作\(-1\)和\(×2\),要求最少操作次数
无脑解法是BFS,不能解决稍大的规模
当n>m时,输出n-m
否则逆向处理,转换为m到n的最小操作次数,存在两种操作\(+1\)和\(/2\)(后者只能在偶数时操作)
由\((m+1+1)/2=m/2+1\)得尽量多的/2操作可以减少操作次数
因此若操作当前的\(m?\)是偶数时尽量/2,直到\(m≤n?\)时再多操作\((n-m)?\)次\(+1?\)是最优操作
Challenge: suppose we have a generalized problem: we want to get n starting from m using two operations "subtract a" and "multiply by b". Generalize the solution to find the minimal number of moves to get from n to m in 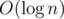 time if a and b are coprime. Can you do it if a and b may have common divisors greater than 1?
time if a and b are coprime. Can you do it if a and b may have common divisors greater than 1?
给出砝码,限定重量类型但个数无限,求能否在天平上按照规则操作\(m\)次并输出方案
规则1.每次使用的砝码不能与上一次的相同重量
规则2:每次放入砝码后该侧的重量比另一侧天平的重量大
我的想法:设\(dp[i][j][k]\):第\(i\)次放入重量为\(j\)的砝码使另一侧的天平为\(k\)
\(dp[i][j][k]=dp[i-1][x≠j][y<sum...]\)
但官方题解用到了平衡的想法来替代sum
那么\(dp[i][j][k]\):存在第\(i\)次放入重量为\(j\)的砝码使两侧平衡差为\(k\)的方案
\(dp[i][j][k]=dp[i-1][x≠j][y=j-k>0]\) ,只需存在一对\((x,y)\)该方程既为真
说明:记上一次平衡差为\(y\),假设砝码放在左边,则\(l-r=y\)
这次在右边平衡差为\(k\),则\(r‘-l‘=k,l‘=l,r‘=r+j\)
\(∴y=j-k\)
给定一个图,顶点数\(n≤500\),图中每对顶点都有两条边分别指向从对中某一点指向另一点,且权值给出
再给定一个删除序列\(x[1...n]\),表示要按顺序删除某个点,求每次序列操作前剩余的所有点对的最短距离之和
逆向思维,考虑floyd三重循环最外层为加入顶点的顺序,那我们把删除序列翻转过来就变为添加序列,既是一个floyd的过程
实现细节上的注意,添加\(x[k]\)点后先把\(x[k]\)相关的所有边都优先松弛再进行内循环更新
PS.做完这道题后对floyd的细节有了船新的认识
https://paste.ubuntu.com/p/YVHzf8pk8R/
从起点走到终点,其中有些地方不能走,有些地方存在一些敌人(0~9),且能和我们一样正常移动或者是停留,每次动作都是一个单位的时间,而敌人总是尽量杀向你。求起点到终点能最少干掉敌人的数目。
要注意到的一点是必然能拦截自己的肯定是它们到终点的距离小于自己到终点的距离
然后从终点BFS就ok了
构造一个n个点m条边的图,使得其1到n最短路距离为素数,MST之和为素数,且没环和重边
很显然构造一条链凑数就好
Last UPD:7.1
标签:src 顶点 ber can 自己 ali tps load class
原文地址:https://www.cnblogs.com/caturra/p/9249243.html