标签:多类别 ted 实现 origin number 抽样 win 一个 nump
更多风控建模、大数据分析等内容请关注公众号《大数据风控的一点一滴》
在分类问题中常常遇到一个比较头疼的问题,即目标变量的类别存在较大偏差的非平衡问题。这样会导致预测结果偏向多类别,因为多类别在损失函数中所占权重更大,偏向多类别可以使损失函数更小。
处理非平衡问题一般有两种方法,欠抽样和过抽样。欠抽样方法可以生成更简洁的平衡数据集,并减少了学习成本。但是它也带来了一些问题,它会删掉一些有用的样本,尤其当非平衡比例较大时,删掉更多的样本会导致原始数据的分布严重扭曲,进而影响分类器的泛化能力。
因此,后来发展出了过抽样方法,它不会删除多类别的样本,而是通过复制少类别样本的方法处理非平衡问题。但是,应用随机过抽样方法复制少类别样本意味着对少类别样本赋予更高的权重,容易产生过拟合问题。
2002年,研究者提出了SMOTE(Synthetic Minority Oversampling Technique)方法来替代标准的随机过抽样方法,可以一定程度克服随机过抽样带来的过拟合问题,提高分类器的泛化能力。SMOTE方法通过在少类别样本的近邻中应用插值法创造新的少类别样本,而不再是简单的复制或赋予权重。
SMOTE算法的步骤如下:
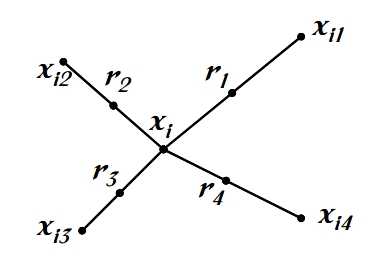
(1)选取第i个少类别样本在所有少类别样本中的K个近邻
(2)从K个近邻中随机选择N个样本,和第i个样本通过插值法获取N个新样本
(3)重复步骤(1)和(2)直到所有少类别样本被遍历一遍
见下图:
SMOTE算法的伪代码:
#============================== SMOTE算法伪代码 ===============================# Algorithm 1 SMOTE algorithm 1: function SMOTE(T, N, k) Input: T; N; k # T:Number of minority class examples # N:Amount of oversampling # K:Number of nearest neighbors Output: (N/100) * T # synthetic minority class samples Variables: Sample[][] # array for original minority class samples; newindex # keeps a count of number of synthetic samples generated, initialized to 0; Synthetic[][] # array for synthetic samples 2: if N < 100 then 3: Randomize the T minority class samples 4: T = (N/100)*T 5: N = 100 6: end if 7: N = (int)N/100 # The amount of SMOTE is assumed to be in integral multiples of 100. 8: for i = 1 to T do 9: Compute k nearest neighbors for i, and save the indices in the nnarray 10: POPULATE(N, i, nnarray) 11: end for 12: end function Algorithm 2 Function to generate synthetic samples 1: function POPULATE(N, i, nnarray) Input: N; i; nnarray # N:instances to create # i:original sample index # nnarray:array of nearest neighbors Output: N new synthetic samples in Synthetic array 2: while N != 0 do 3: nn = random(1,k) 4: for attr = 1 to numattrs do # numattrs:Number of attributes 5: Compute: dif = Sample[nnarray[nn]][attr] ? Sample[i][attr] 6: Compute: gap = random(0, 1) 7: Synthetic[newindex][attr] = Sample[i][attr] + gap * dif 8: end for 9: newindex + + 10: N ? ? 11: end while 12: end function
SMOTE算法的python实现:
下面用python实现一个SMOTE的最简单的版本:
####### python3.6 ######## import random import numpy as np from sklearn.neighbors import NearestNeighbors def smote_sampling(samples, N=100, K=5): n_samples, n_attrs = samples.shape if N<100: n_samples = int(N/100*n_samples) indx = random.sample(range(len(samples)), n_samples) samples = samples[indx] N = 100 N = int(N/100) synthetic = np.zeros((n_samples * N, n_attrs)) newindex = 0 neighbors=NearestNeighbors(n_neighbors=K+1).fit(samples) for i in range(n_samples): nnarray=neighbors.kneighbors(samples[i].reshape(1,-1),return_distance=False)[0] for j in range(N): nn = random.randint(1, K) dif = samples[nnarray[nn]]- samples[i] gap = random.random() synthetic[newindex] = samples[i] + gap * dif newindex += 1 return synthetic
python中imblearn模块对SMOTE算法的封装
python 中有封装好的SMOTE方法,在实践中可以直接调用该方法,具体参数可以查看官方文档。简单应用举例:
from sklearn.datasets import make_classification from collections import Counter from imblearn.over_sampling import SMOTE # 生成数据集 X, y = make_classification(n_classes=2, class_sep=2, weights=[0.1, 0.9], n_informative=3, n_redundant=1, flip_y=0, n_features=20, n_clusters_per_class=1, n_samples=1000, random_state=9) # 类别比例 Counter(y) # SMOTE合成新数据 sm = SMOTE(ratio={0: 900}, random_state=1) X_res, y_res = sm.fit_sample(X, y) # 新数据类别比例 Counter(y_res)
标签:多类别 ted 实现 origin number 抽样 win 一个 nump
原文地址:https://www.cnblogs.com/bigdatafengkong/p/9251117.html