机器学习（一）—— 线性回归

标签：模型   由来   str   身高   数据处理   归一化   集中   缩减   包括   

机器学习（一）—— 线性回归

目录

0. 回归（Regression）的由来

1. 回归关系

2. 线性回归的整体思路

（1）根据数据提出假设模型

（2）求解参数

      1）梯度下降法

      2）正规方程求解参数

（3）梯度下降法与正规方程比较

3. 回归的一般方法

4. 实例分析

5. 线性回归的特点及其优缺点

6. 代码实现（Java）

（本文是基于吴恩达老师的机器学习课程整理的）

0. 回归（Regression）的由来

*********************************“回归”一词的来源************************************

　　今天所知道的回归是由达尔文（Charles Darwin）的表兄弟Francis Galton发明的。Galton于1877年完成了第一次回归预测，目的是根据上一代豌豆种子（双亲）的尺寸来预测下一代豌豆种子（孩子）的尺寸。Galton在大量对象上应用了回归分析，甚至包括人的身高。他注意到，如果双亲的高度比平均高度高，他们的子女也倾向于比平均高度高，但尚不及双亲。孩子的高度向着平均高度回退（回归）。Galton在多项研究上都注意到这个现象，所以尽管这个英文单词跟数值预测没有任何关系，但这种研究方法仍被称为回归。

******************************************************************************************

　　Regression有“衰退，退步”的意思，Galton在研究父母身高和子女身高时发现，即使父母的身高相对于人群平均身高来说很高，子女的身高比平均值高，但是却比父母低，即有种向平均值（正常身高）靠近（“衰退”）的倾向。

　　具体地，Galton和他的学生Pearson在研究父母身高（单位：英寸）与其子女身高的遗传问题时，观察了1078对夫妇，以每对夫妇的平均身高作为x，而取他们的一个成年儿子的身高作为y，将结果在平面直角坐标系上绘成散点图，发现趋势近乎一条直线，计算出的回归直线方程为y=33.73+0.516x。这种趋势及回归方程总的表明父母平均身高x每增加一个单位，其成年儿子的身高y也平均增加0.516个单位。这个结果表明，虽然高个子父辈确有生高个子儿子的趋势，但父辈身高增加一个单位，儿子的身高仅增加半个单位左右。反之，矮个子父辈确有生矮个子儿子的趋势，但父辈身高减少一个单位，儿子身高仅减少半个单位左右。即子代的平均高度向中心回归了。

 1.回归关系

　　在客观世界中普遍存在着变量之间的关系，变量之间的关系一般来说可以分为两种：

　　①确定性的：变量之间的关系可以用函数关系来表达；

　　②非确定性的：即统计关系或相关关系。如，人的身高与体重的关系，一般来说人高一些，体重也要重一些，但是也存在同样高度的人，体重有高有低，即没有明确的函数关系。现代统计学中关于统计关系已形成两个重要的分支，它们叫相关分析和回归分析。

　　回归分析就是研究统计关系的一种数学工具，能帮助我们从一个变量（预测变量或回归变量，可以理解为自变量）取得的值去估计另一个变量（响应变量，可以理解为因变量）所取的值。且自变量与因变量均为连续变量。当自变量只有一个变量时，我们称该回归为一元回归，当自变量有多个变量时，称为多元回归。若使用线性函数刻画自变量和因变量之间的相关关系，则称为线性回归，否则称为非线性回归。所以模型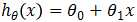，称为一元线性回归模型（或简单线性回归模型），模型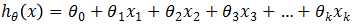，称为多元线性回归模型，其中，参数θ₀称为回归常数，θ₁, θ₂, … ,θ_k称为回归系数。注意，其中“线性”是用来表明模型的参数θ₀, θ₁, θ₂, …, θ_k是线性的，而非y是关于x的线性函数。许多模型中y与x以非线性形式相关，但只要方程关于θ是线性的（也就是说不管x是几次方，只要所有参数θ均为一次方）就仍然可以将其当做线性回归方程处理，因为当回归变量为非线性时，可以通过变量替换将它转化为线性的。

　　需要注意的是：回归模型并非意味着变量间存在因果关系。即使两个或更多变量间可能存在牢固的实证关系，也不能认为这就证明了回归变量与响应变量间存在因果联系。确立因果关系，要求回归变量与响应变量必须存在一种基础性的、与样本数据无关的关系，比如理论分析中所暗含的关系。回归分析有助于因果关系的确认，但不能成为判断因果关系是否存在的唯一基础。

　　一定要记住，回归分析只是众多用于解决问题的数据分析方法的一种，也就是说，回归方程本身可能并非研究的主要目的，就整个数据处理过程而言，洞察力与理解力通常更为重要。

 2. 线性回归的整体思路

（1）根据数据提出假设模型

　　上面已经知道，回归的目的是通过几个已知数据来预测另一个数值型数据的目标值。下面通过例子阐述线性回归的思想及过程。

　　假设我们有如下表1所示的训练集，其中自变量x为房子的面积（单位feet²），因变量为房子的卖价（单位$1000），共有M个样本。

　　表 1  训练集样本（M个样本）

　　通过观察，我们发现，随着x增大，相应的y也增大，所以我们设想x和y应该满足线性关系，即假设模型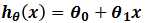可以描述x和y之间的线性关系，其中θ₀，θ₁为模型的参数。接下来只需要求解出参数θ₀，θ₁，就可以为新样本x`预测相应的房价h<sub>θ</sub>(x`)，即y`。

（2）求解参数

　　使用回归分析的一个重要目标是估计模型中的未知参数，这一过程也称为模型拟合数据。

　　1）梯度下降法

求解参数的原则

　　模型有了，就差参数了，那该如何求解呢？我们先看看求解参数θ₀，θ₁，的原则是什么。因为模型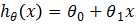描述的是x和y之间的关系，即越能准确的刻画x与y的关系，那么模型越好，那怎么来判断是否准确呢？若对于每一个x，模型预测出的h_θ(x)=y，那么无疑该模型非常好，因为它能准确的反应我们训练集中所有样本的情况，若是对于未知的x，也能准确的预测出相应的y，那么该模型堪称完美。可惜这种情况是不存在的，因为在我们收集数据时，会由于各种各样的原因，造成数据误差（如测量误差）或者包含噪声等后果，所以模型达不到h_θ(x)=y这种理想情况，通常h_θ(x)-y≠0，我们当然希望这个差值越小越好，那就要调整h_θ(x)，所以就需要调整θ₀，θ₁，到这就明白了，调整参数θ₀，θ₁的目的（原则）是使模型预测值更接近真实值y，即使差值更小。

代价函数（cost function）

　　接下来我们需要衡量模型预测值与真实值之间的差异，通过直接求差值h_θ(x)-y来计算一个样本的差是可以的，但是要衡量整个训练集的差异就会存在正负相抵消的问题，那么用绝对值呢？绝对值没有正负抵消问题，但是在后面的计算中求导是分段函数，相对比较麻烦，所以也不用。考虑差值的次方，因为奇数次方都会存在正负抵消问题，所以来看偶数次方，偶数次方没有之前的那些问题，但是考虑到计算的简便性，我们用平方来计算二者之间的差异，即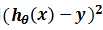，也称该函数为平方损失函数。同时，平方损失函数还有个好处是可以惩罚那些差值较大的项，比如(10-5)²=25，(10-8)²=4，25:4相较于5:2更能突出差异大的点。

　　接下来，我们用平方损失函数对每一个样本计算差异（损失），再求和取平均作为整体训练集对参数θ₀，θ₁的损失J(θ₀, θ₁)，公式为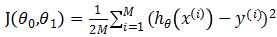：，其中公式中的1/2是为了后续求导计算中约掉指数上的2，x⁽ⁱ⁾，y⁽ⁱ⁾表示第i个样本。我们称J(θ₀, θ₁)为代价函数（cost function），其反映了训练集所有样本在参数θ₀，θ₁下的平均损失。因为我们需要模型能较为准确的表示变量之间的关系，也即模型预测值与真实值之间的差异要尽可能的小，所以我们需要J(θ₀, θ₁)尽可能的小，也就是说，现在将从假设模型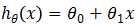中直接求参数θ₀，θ₁转化为在代价函数J(θ₀, θ₁)中求解参数θ₀，θ₁，使代价函数J(θ₀, θ₁)最小。

代价函数J(θ₀, θ₁)和模型h_θ(x)之间的关系

 　　首先模型h_θ(x)是给定参数θ下，关于x的函数，而J(θ₀, θ₁)是关于θ₀，θ₁的函数。给定参数θ₀，θ₁，可以计算出一个J(θ₀, θ₁)。为了方便表示和理解，我们假设参数θ₀=0，即模型是过原点的直线，设样本点为(1, 1), (2, 2), (3, 3)，接下来，我们取不同的θ₁来计算J(θ₁)。

　　如下图1所示，黑色线表示θ₁=1，三个样本点刚好全都落在该直线上，其代价函数值为0，所以J(θ₁)过点(1, 0)，蓝色直线斜率为0.5，其代价函数值为0.58，所以J(θ₁)过点(0.5, 0.58)，同样绿色直线斜率为2，其代价值为7/3，所以J(θ₁)过点(2, 7/3)，得到的代价函数如图2所示。若不设θ₀=0，则J(θ₀, θ₁)的等高线如图3所示。

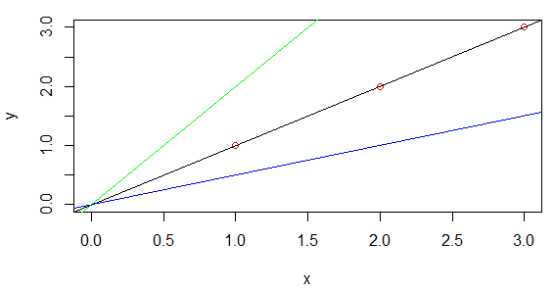
图 1 不同参数下的模型

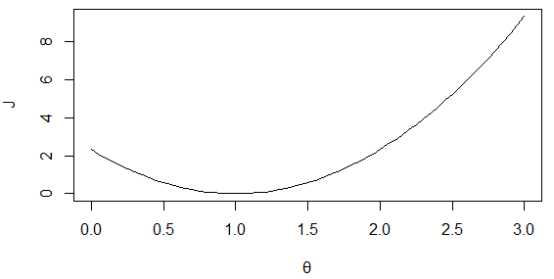
图 2 代价函数J(θ₁)

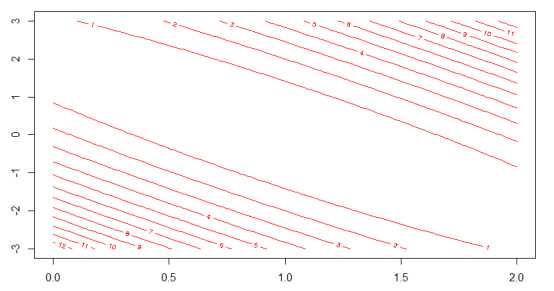
图 3 J(θ₀, θ₁)的等高线，横轴为θ₁，纵轴为θ₀

利用代价函数求解参数

　　我们的目的是求得参数θ₀，θ₁，使代价函数J(θ₀, θ₁)值最小。即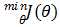，因为线性回归的代价函数J(θ)总是凹面，即凸函数，最小化J(θ)属于凸优化，我们用最经典的梯度下降算法。

梯度下降法的思路：

• 给参数θ₀，θ₁初始值，常设为（0, 0）
• 调整θ₀，θ₁使J(θ₀, θ₁)减小
• 直到代价函数J(θ₀, θ₁)减小到最小值

　　为什么要设置初始值为0呢？因为后续都会调整参数来求代价函数的最小值，而且先前我们也不知道要具体设置为多少，所以遵循简单原则，设置为0。接下来调整参数，如下：

　　重复以下步骤直到收敛{

　　}

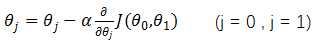
　　α为下降步长，也叫学习率（learning rate），它决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。偏导数项是用来保证以直线方向下降（最快下降方向）。

　　我们来看看α产生的影响，同样的，设θ₀=0，在之前图2中会产生以下收敛方式，因为J(θ)图形变化比较缓慢，所以会随着导数项减小而减小，如图4所示，经多次减小后，越到最小值附近，J(θ)变化越缓慢。但是对于图5来说，J(θ)比较陡峭，变化较快，在接近最低点的时候导数值依然很大。即α过大，可能会引起振荡，找不到极值点，α过小，会导致收敛时间太长。那么要怎么选取合适的α呢？吴恩达老师给的建议是从[0.001, 0.003, 0.01, 0.03, 0.1, 0.3…]中选择。在实验过程中可以通过判断第i次更新后的代价值是否小于第i-1次，若小于，可以稍微增大一点α，以更快的收敛；若大于，则需要减小α，防止发生振荡。

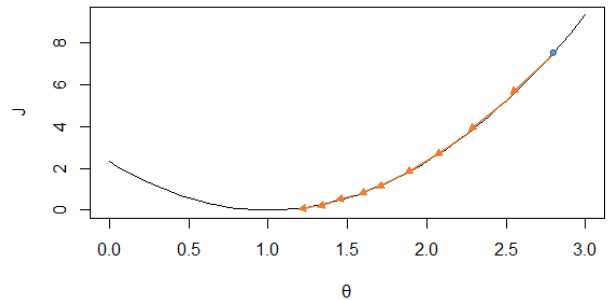
图 4 变换缓慢的J(θ)上的收敛过程

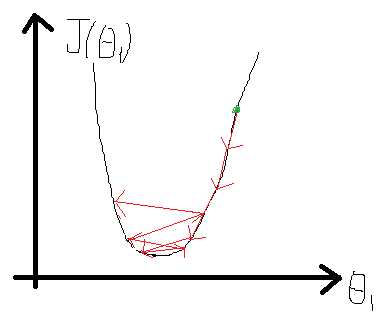
图 5 比较陡峭的J(θ)上的收敛过程

　　接下来，我们用一个例子说明梯度下降方法。求y=(x-1)²的最小值点，选步长为0.5：

　　① 设初始值x₀=0，则y=1，在x=0处梯度值为-2，

　　② 更新x₁=0-0.5*(-2)=1，则y=0，此处梯度值为0，找到最小值点（1,0）

　　接下来我们如何判断收敛呢？对于一般的数学函数来说，只要导数值为0即可，但是对于1/x这类函数来说，有两种方式来判断其是否收敛，一种是看J(θ)的函数图形，如果基本没有变化，则可认为是收敛；另一种为设置变化阈值ε，如ε<0.001，若两次相邻的J(θ)变化小于ε，则可认为是收敛了，但是如何确定ε的大小则比较困难。

多元线性回归

　　之前描述的是一元线性回归，那么如何对多元变量进行线性回归呢？如下表2的训练数据：

表2 多维特征数据

　　此时假设模型函数为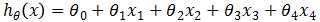，代价函数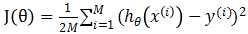：，其中θ为5维向量，优化与求解与之前一样。

　　需要注意的是，因为特征中x₁, x₂之间的取值范围差异太大，得到的J(θ)性状窄长（因为取值范围一大一小），会导致收敛产生振荡，如下图6所示（手画，比较丑）。

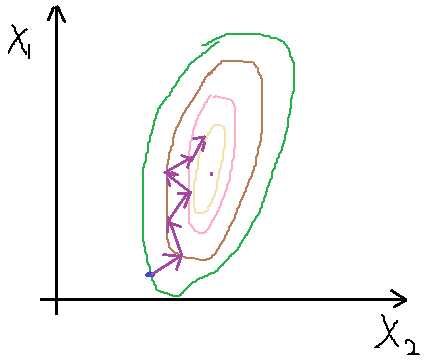
图 6 特征取值范围较大时会出现振荡

　　产生振荡会使收敛不到最小点处，因此为了避免这种情况，我们需要对特征进行缩放，也相当于归一化处理，使他们的取值范围都在一个区间，通常我们将特征值除以该特征的最大值与最小值的差。比如若x1取值范围为650--3000，缩放为：x1/(3000-650)。缩放后代价函数变得相对圆些，如图7 所示，其收敛过程就相对平滑，也能较快收敛到最小值点。

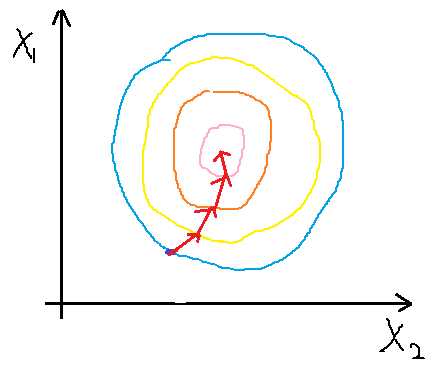
图 7 特征缩放后的收敛相对平缓

　　2）正规方程求解参数

　　对于表2中的数据，我们添一列x₀，使其全为1，模型写为：h_θ(x) = θ₀x₀+θ₁x₁+θ₂x₂+θ₃x₃+θ₄x₄。我们记矩阵

　　其中，每一行为一个样本的所有特征，X称为设计矩阵（design matrix），为m*(n+1)型矩阵，其中m是训练集样本数，n为样本的特征数（不包括x₀）。记向量y=(460, 232, 315, 178, …)^T，即y为m*1型，同样记θ=(θ₀, θ₁，θ₂, θ₃, θ₄)为（n+1）*1型，类似于梯度下降的优化目标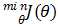，有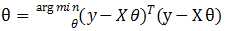，令E_θ=(y-Xθ)^T(y-Xθ)，对θ求导得到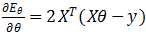，令其为0，可得到θ的最优解，θ=(X^TX)^-1X^Ty，但是X^TX的逆是否一直存在呢？其实不是的，当矩阵X中存在冗余的特征，那么就不可逆，还有，当m≤n，即特征数太多，对于这两种情况，都可以通过删除特征解决，对于冗余特征来说，我们删除掉冗余的特征，第二种情况除过删除特征外，还可以使用正则化的方式解决： θ=(X^TX+λB)^-1X^Ty，其中B为(n+1)*(n+1)型矩阵，其对角线上除B₁₁外均为1，其余为0，则括号内的矩阵绝对可逆。

（4）梯度下降法与正规方程比较

 3. 回归的一般方法

（1） 收集数据：采用任意方法收集数据；

（2） 准备数据：回归需要数值型数据，标称型数据将被转成二值型数据；

（3） 分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后，可以将新拟合线绘在图上作为对比；

（4） 训练算法：找到回归系数；

（5） 测试算法：使用R²或者预测值和数据的拟合度，来分析模型的效果；

（6） 使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

 4. 实例分析

　　为了可视化效果，我们只使用一个特征（size of feet²）来说明线性回归的实例应用。

（1） 收集数据：我们根据现实生活的情况，设定了20个样本，如下表3所示：

表3 训练样本集

（2） 准备数据：数据已是数值型数据；

（3） 分析数据：将其可视化如下图8.

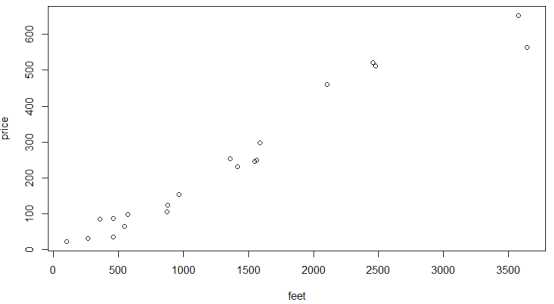
图8 训练集数据的可视化

（4） 训练算法：

　　我们的假设为h_θ(x)=θ₀+θ₁*x，优化的目标函数为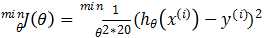 ，根据梯度下降法，通过判断参数更新前后的代价函数差值来看是否α取得过大，即差值小于零，表示更新完参数后，代价值增加，说明有振荡产生，因此再减小α。经过试验，取学习率（下降步长）为10^-6，当连续两次代价函数差小于10^-6作为收敛条件，求得θ₀=-10.13，θ₁=0.18，此时的代价J(θ)=890.81

（5） 测试算法：

　　我们将得到的h_θ(x)与样本点画出来，如下图9.可以看出效果不错，毕竟事实就是房子面积越大，卖价越高，当然还有地段等因素影响，所以并不是完全都在直线上。

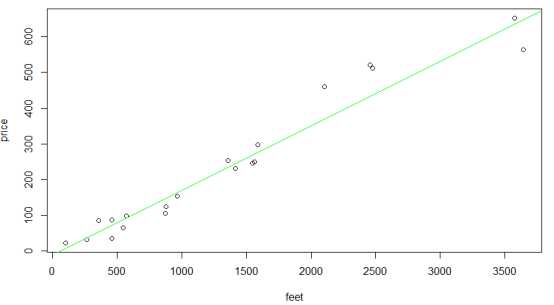
图 9 样本点与回归线

（6） 使用算法：我们用得到的线性模型对新样本x=2000，来预测该面积的房子卖价y=h_θ(x)=-10.13+0.18*2000=349.87，注意单位是千$。

5.线性回归的特点及其优缺点

使用数据类型：数值型和标称型数据

优点：

结果易于理解，计算上不复杂；

可以根据系数理解每个变量；

缺点：

对非线性的数据拟合不好；

对异常值非常敏感；

受噪声影响大；

只能表示线性关系；

 6. 代码实现（Java）

 https://www.cnblogs.com/datamining-bio/articles/9240378.html

机器学习（一）—— 线性回归

标签：模型   由来   str   身高   数据处理   归一化   集中   缩减   包括   

原文地址：https://www.cnblogs.com/datamining-bio/p/9256302.html