标签：阈值 正交 .com 解决 操作 表达 问题 观察 不同
一 霍夫直线变换
1 点斜式
直线方程可表示为：y = kx + b， 当k, b确定时，在xy平面上确定一条唯一直线；考虑同样的变形 b = -xk + y，当x, y确定时，可以看做在kb平面上确定的一条唯一直线；若x, y表示xy平面上一个已知坐标点，则经过该坐标点(x, y)可形成多条直线， 其表达式为：b = -xk + y。
考虑在平面图像上存在一条有效直线段，遍历图像上每一个点，并计算出每个点可能形成的直线参数；发现某个特定参数(k, b)出现次数最多，这个特定参数应该为图像上有效直线段的参数(k, b)。
通过以上观察，可以将参数(k, b)离散化，然后遍历平面图像上的每一个点，累加可能形成直线(k, b)参数；当遍历完整个图像后，在累加器(k, b)中会产生一个全局最大值，该值为平面图像上有效直线的参数(k, b)。
当平面图像上存在多条有效直线段时，在累加器(k, b)中会产生多个局部极大值，可以通过设定合理的阈值以检测出平面图像上的多条直线段。
2 极坐标
使用点斜式检测直线存在两个问题：
1）y = kx + b 无法表达平行于y轴的直线段（k为无穷大）；
2）k, b取值都趋近于无穷大，离散化(k, b)后参数空间趋近无穷大，计算机存储空间有限；
通过坐标转换，将直角坐标转换为极坐标可以解决以上问题。
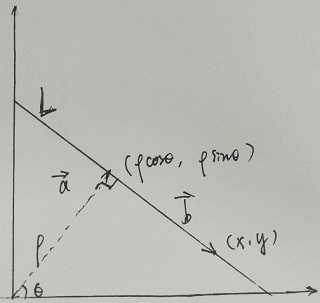
根据图形可得：ab = 0 (向量a与向量b正交）
=>
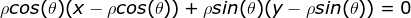， 其中(x, y)为直线L上的任意点；
=>
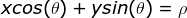， 其中(x, y)为直线L上的任意点；
考虑在平面图像上存在一条有效直线段，离散化参数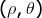
，然后遍历平面图像上每一个点，累加可能形成的直线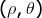参数；类似的，在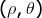平面上会产生一个全局最大值，该值即为平面图像上的有效直线参数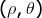；同理，针对平面图像上存在多条有效直线段情况，可以通过局部极大值检测多条有效直线段。
二 霍夫圆变换
圆的方程式可表达为：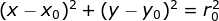
，参数
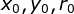确定一个圆；
离散化参数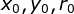，遍历平面图像上每一个点，累加可能形成的圆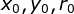参数， 在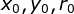参数空间中寻找全局最大值或局部极大值以检测有效圆；
圆的方程也可表达为：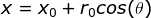
，
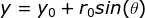，参数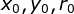确定一个圆；
固定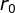
，遍历平面图像上每一个点，根据公式
，
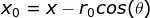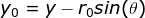累加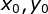 
参数空间，在参数空间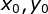寻找全局最大值或局部极大值以检测半径为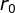的有效圆；
多次遍历平面图像，并选择不同的半径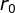可以检测平面图像上任意半径的圆。
三 霍夫变换检测椭圆
平面上任意一个椭圆均可以看做单位圆经过缩放，旋转，平移操作形成，设在单位圆上的坐标点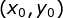
，经过缩放，旋转，平移变换的表达式为：
，
=>
, 
，
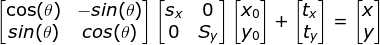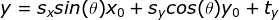表达式构成参数空间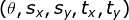
，离散化该参数空间， 遍历平面图像上每一个点，累加可能形成椭圆的参数，在
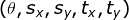参数空间中寻找全局最大值或局部极大值检测椭圆。
以上方法形成的参数空间过大，实现时需要大量的存储空间，需要使用参数空间压缩的方法以便于计算机实现。
标签：阈值 正交 .com 解决 操作 表达 问题 观察 不同
原文地址：https://www.cnblogs.com/luofeiju/p/9262336.html
