标签：ret   int start   递归   剪枝   查找   方案   ...   target   无法   

回溯法

全排列系列

46题:

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例：

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

代码：

public List<List<Integer>> permute(int[] nums) {
   List<List<Integer>> list = new ArrayList<>();
   // Arrays.sort(nums); // 不必先排序
   backtrack(list, new ArrayList<>(), nums);
   return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
   if(tempList.size() == nums.length){
      list.add(new ArrayList<>(tempList));
   } else{
      for(int i = 0; i < nums.length; i++){ 
         if(tempList.contains(nums[i])) continue; // 元素已经存在，跳过
         tempList.add(nums[i]);
         backtrack(list, tempList, nums);
         tempList.remove(tempList.size() - 1);
      }
   }
} 

47题：

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例：

输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

代码：

 public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> temp=new ArrayList<>();
        boolean[] used=new boolean[nums.length]; //指示该值是否已经添加到列表中
        Arrays.sort(nums);     //对数组排序，确保可以跳过相同的值
        helper(res,temp,used,nums);
        return res;

    }
    public void helper(List<List<Integer>> res,List<Integer> temp,boolean[] used,int[] nums){
        if (temp.size()==nums.length){
            res.add(new ArrayList<>(temp));
        }else {
            for (int i = 0; i <nums.length ; i++) {
                //列表中已经添加过这个位置的值，跳过
                if (used[i]) continue;
                //当一个数字与之前的数字具有相同的值时，我们只有在使用前一个数字时才能使用此数字
                if (i>0&&nums[i]==nums[i-1]&&!used[i-1]) continue;  
                
                used[i]=true;
                temp.add(nums[i]);
                helper(res,temp,used,nums);
                used[i]=false;
                temp.remove(temp.size()-1);
            }
        }
    }

子集系列

78题：

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集。 说明：解集不能包含重复的子集。

示例：

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

代码：

public List<List<Integer>> subsets(int[] nums) {
    List<List<Integer>> list = new ArrayList<>();
   // Arrays.sort(nums);//不必要
    backtrack(list, new ArrayList<>(), nums, 0);
    return list;
}

private void backtrack(List<List<Integer>> list , List<Integer> tempList, int [] nums, int start){
    //先存结果，递归边界不用显式确定，如果无法添加自然不会再递归
    list.add(new ArrayList<>(tempList));
    for(int i = start; i < nums.length; i++){
        tempList.add(nums[i]);
        backtrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);
    }
}

另一种迭代方法

代码：

public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        result.add(new ArrayList<>());
        for(int n : nums){
            int size = result.size();
            for(int i=0; i<size; i++){
                List<Integer> subset = new ArrayList<>(result.get(i));
                subset.add(n);
                result.add(subset);
            }
        }
        return result;
    }

解释：

在迭代所有数字时，对于每个新数字，我们可以选择它，也可以不选择它
1，如果选择，只需将当前编号添加到每个现有子集。
2，如果没有选择，只保留所有现有的子集。
我们只是将两者结合起来。

例如，{1,2,3}在内部我们有一个结果集[[]]
考虑1，如果不使用它，仍然[]，如果使用1，将它添加到[]，所以我们现在有[1]
结合它们，现在我们有[[]，[1]]作为所有可能的子集

接下来考虑2，如果不使用它，我们仍然有[[]，[1]]，如果使用2，只需在每个前面的子集中加2，我们有[2]，[1,2]
结合他们，现在我们有[[]，[1]，[2]，[1,2]]

接下来考虑3，如果不使用它，我们仍然有[[]，[1]，[2]，[1,2]]，如果使用3，只需在每个前面的子集中加3，我们[[3]， [1,3]，[2,3]，[1,2,3]]
结合它们，现在我们有[[]，[1]，[2]，[1,2]，[3]，[1,3]，[2,3]，[1,2,3]]

90题：

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。说明：解集不能包含重复的子集。

示例：

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

代码：

public List<List<Integer>> subsetsWithDup(int[] nums) {
    List<List<Integer>> list = new ArrayList<>();
    Arrays.sort(nums);//排序必要，跳过重复
    backtrack(list, new ArrayList<>(), nums, 0);
    return list;
}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int start){
    list.add(new ArrayList<>(tempList));
    for(int i = start; i < nums.length; i++){
        if(i > start && nums[i] == nums[i-1]) continue; // 跳过重复元素（剪枝）
        tempList.add(nums[i]);
        backtrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);
    }
} 

另一种迭代方法：（在78题迭代法上改进）

代码：

public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);  //不要忘了排序
        List<List<Integer>> result = new ArrayList<>();
        result.add(new ArrayList<>());
        int size=0;
        for(int j=0;j<nums.length;j++){
            
            int start =(j>=1&&nums[j]==nums[j-1])?size:0;  //定起始位置，这里的size还没更新，所以是上一次迭代后的结果数目
            size=result.size();  //size用来保存当前结果数目
            for(int i=start; i<size; i++){
                List<Integer> subset = new ArrayList<>(result.get(i));
                subset.add(nums[j]);
                result.add(subset);
            }
        }
        return result;
    }

组合系列

组合 77题：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例：

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

代码：

public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res=new ArrayList<>();
        helper(res, new ArrayList<Integer>(),1,n,k);
        return res;

    }
    private void helper(List<List<Integer>> res,List<Integer> templist,int start,int n,int k){
        if (k==0){
            res.add(new ArrayList<>(templist));
            return;
        }
        for (int i=start;i<=n;i++){
            templist.add(i);
            helper(res,templist,i+1,n,k-1);
            templist.remove(templist.size()-1);
        }
    }

组合总和系列：

组合总和1：39题：

给定一个无重复元素的数组** candidates** 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：所有数字（包括 target）都是正整数。解集不能包含重复的组合。

示例：

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

代码：

public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);       //先排序便于跳过大于target的数字
        List<List<Integer>> res=new ArrayList<>();      
        getRes(res,new ArrayList<Integer>(),candidates,target,0);
        return res;

    }
    private void getRes(List<List<Integer>> res, List<Integer> cur,int[] candidates,int target,int start){
        if (target>0){
            for (int i=start;i<candidates.length&&target>=candidates[i];i++){     //从start开始往后找
                cur.add(candidates[i]);
                getRes(res,cur,candidates,target-candidates[i],i);
                cur.remove(cur.size()-1);  //调用返回后及时清除
            }
        }else if (target==0){
            res.add(new ArrayList<>(cur));  //此处不能res.add(cur) 只能添加cur的副本，不然对cur的remove会改变res中相应添加的项
        }
    }

组合总和2 ：40题：

题目同1，但是candidates 中的每个数字在每个组合中只能使用一次。

示例：

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

代码：

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> res=new ArrayList<>();
        getRes(res,new ArrayList<Integer>(),candidates,target,0);
        return res;

    }
    private void getRes(List<List<Integer>> res, List<Integer> cur,int[] candidates,int target,int start){
        if (target>0){
            for (int i=start;i<candidates.length&&target>=candidates[i];i++){
                if (i>start&&candidates[i]==candidates[i-1]){ continue;}  //跳过数组中的重复元素（剪枝） 注意从当前start开始
                cur.add(candidates[i]);
                getRes(res,cur,candidates,target-candidates[i],i+1);   //注意是i+1 不能重复使用数组中的元素
                cur.remove(cur.size()-1);
            }
        }else if (target==0){
            res.add(new ArrayList<>(cur));
        }
    }

组合总和3：216题：

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

示例：

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

代码：

public List<List<Integer>> combinationSum3(int k, int n) {
    int[] num = {1,2,3,4,5,6,7,8,9};
    List<List<Integer>> result = new ArrayList<List<Integer>>();
    helper(result, new ArrayList<Integer>(), num, k, n,0);
    return result;
    }

public void helper(List<List<Integer>> result, List<Integer> list, int[] num, int k, int target, int start){
    if (k == 0 && target == 0){
        result.add(new ArrayList<Integer>(list));
    } else {
        for (int i = start; i < num.length && target > 0 && k >0; i++){
            list.add(num[i]);
            helper(result, list, num, k-1,target-num[i],i+1);
            list.remove(list.size()-1);
        }
    }
}

涉及字符串的回溯问题

括号生成 22题：

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

思路：最初的想法是生成所有的组合情况，再写辅助函数判断是否合法。但这么做不必要，因为给定了括号的对数，只要最后生成的左右括号数都等于括号对数就是合法。可以在递归参数中引入左右括号各自的计数器，来记录数量，在当前Stirng中字符数量达到2*括号对数时，添加结果到list。

代码：

 public List<String> generateParenthesis(int n) {
        List<String> l=new ArrayList<>();
        backcrack(l,"",0,0,n);
        return l;

    }
    public void backcrack(List<String> l,String current,int open,int close,int max){
        if (current.length()==2*max){
            l.add(current);
        }else {
            if (open<max){   //max为括号对数
                backcrack(l,current+‘(‘,open+1,close,max);
            }
            if (close<open){//注意这里 只有右括号的数量小于左括号的数量，才可以加右括号
                backcrack(l,current+‘)‘,open,close+1,max);
            }
        }
    }
    //只生成合法的情况。这里的current相当于数组回溯问题中的List<Integer> templist

注意！：java里边String对象是不可变的，也就是说current+‘(‘不是简单的在原来的current指向的String对象后面加上‘(‘，而是又新生成了一个current+‘(‘，和原来的不是一个了。

电话号码的字母组合 17题：

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例：

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

代码：

private static final String[] KEYS = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
    
        public List<String> letterCombinations(String digits) {
           
            List<String> ret = new LinkedList<String>();
             if(digits == null || digits.length() == 0) return ret;
            combination("", digits, 0, ret);
            return ret;
        }
    
        private void combination(String prefix, String digits, int offset, List<String> ret) {
            if (offset >= digits.length()) {
                ret.add(prefix);
                return;
            }
            String letters = KEYS[(digits.charAt(offset) - ‘0‘)];
            for (int i = 0; i < letters.length(); i++) {
                combination(prefix + letters.charAt(i), digits, offset + 1, ret);
            }
        }
        //这里定义的前缀prefix相当于数组中回溯问题的List<Integer> templist，都是作为递归函数的参数保存生成结果的。

复原IP地址 93题：

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

示例：

输入: "25525511135"
输出: ["255.255.11.135", "255.255.111.35"]

注意：

什么是有效的IP地址格式？

代码：

public List<String> restoreIpAddresses(String s) {
        List<String> res = new ArrayList<>();
        helper(s,"",res,0);
        return res;
    }
    public void helper(String s, String tmp, List<String> res,int n){
        if(n==4){
            if(s.length()==0) res.add(tmp.substring(0,tmp.length()-1));
            //substring here to get rid of last ‘.‘
            return;
        }
        for(int k=1;k<=3;k++){
            if(s.length()<k) continue;  //剪枝
            int val = Integer.parseInt(s.substring(0,k));
            if(val>255 || k!=String.valueOf(val).length()) continue;
            /*in the case 010 the parseInt will return len=2 where val=10, but k=3, skip this.*/
            helper(s.substring(k),tmp+s.substring(0,k)+".",res,n+1);
            //每次递归，s都是传的k起始的一个子串，这样传参更简便，不用麻烦地传s下标
        }
    }

分割回文串 131题：

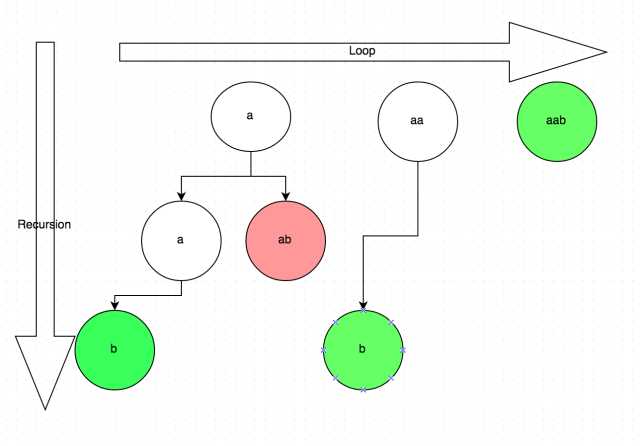
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

示例：

输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

代码：

   public List<List<String>> partition(String s) {
        List<List<String>> res=new ArrayList<>();
        List<String> cur=new ArrayList<>();
        helper(res,s,cur,0,s.length());
        return res;
    }
    //判断回文字符串的辅助函数
    public boolean isPalindrome(String s){
        int n=s.length()-1,i=0;
        while (i<n){
            if (s.charAt(i)!=s.charAt(n)){
                return false;
            }
            i++;
            n--;
        }
        return true;

    }
    
    //回溯函数
    public List<List<String>> helper(List<List<String>> res, String s,List<String> cur,int start,int len){
        if (start==len){
            res.add(new ArrayList<>(cur));
        }
        for (int i=start+1;i<=len;i++){
           if (isPalindrome(s.substring(start,i))){
               cur.add(s.substring(start,i));
               helper(res,s,cur,i,len);
               cur.remove(cur.size()-1);
           }
        }
        return res;
    }

图解：

其他问题：

单词搜索 79题：

给定一个二维网格和一个单词，找出该单词是否存在于网格中。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例：

board =
[
  [‘A‘,‘B‘,‘C‘,‘E‘],
  [‘S‘,‘F‘,‘C‘,‘S‘],
  [‘A‘,‘D‘,‘E‘,‘E‘]
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

分析：实际上这道题属于DFS 在一个二维数组里面做查找

代码：

static boolean[][] visited;
    public boolean exist(char[][] board, String word) {
        visited = new boolean[board.length][board[0].length];
        
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[i].length; j++){
                if((word.charAt(0) == board[i][j]) && search(board, word, i, j, 0)){
                    return true;
                }
            }
        }
        
        return false;
    }
    
    private boolean search(char[][]board, String word, int i, int j, int index){
        if(index == word.length()){
            return true;     //查找到最后 说明找到 返回
        }
        
        if(i >= board.length || i < 0 || j >= board[i].length || j < 0 || board[i][j] != word.charAt(index) || visited[i][j]){
        //下标越界，当前搜索位置的字母与目标字母不同，当前位置字母已经访问过 这些情况都属于没找到，返回flase
            return false;
        }
        
        visited[i][j] = true;    //置为已访问
        if(search(board, word, i-1, j, index+1) || 
           search(board, word, i+1, j, index+1) ||
           search(board, word, i, j-1, index+1) || 
           search(board, word, i, j+1, index+1)){
            return true;   //有一路找到就直接返回就行 最终一定是找到了 就不用管visited是不是置回false了
        }
        
        visited[i][j] = false;    //递归回溯后记得再置回未访问 以便再找另一路
        return false;  //进行到这一步还没return 这一路是最终没找到
    }

格雷编码 89题：

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。
给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

示例：

输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。
     给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。
     因此，当 n = 0 时，其格雷编码序列为 [0]。

分析：这题标签是回溯法，但实际上回溯不是最好的办法。

代码：

public List<Integer> grayCode(int n) {
    List<Integer> rs=new ArrayList<Integer>();
    rs.add(0);
    for(int i=0;i<n;i++){
        int size=rs.size();
        for(int k=size-1;k>=0;k--)
            rs.add(rs.get(k) | 1<<i);  //或者写成 rs.add(rs.get(k)+(1<<i))
    }
    return rs;
}

回溯法

标签：ret   int start   递归   剪枝   查找   方案   ...   target   无法   

原文地址：https://www.cnblogs.com/10zhang/p/9264115.html