标签：adr   att   obj   问题   tps   一个   特征   hat   learning   

NMF非负矩阵分解初探

简介

数据可以表示为一个矩阵 $V$，列 $v_n$ 是采样点而行代表特征features。我们想把这个矩阵$V$因式分解为两个未知的矩阵 $W$ 和 $H$

$$ V \approx \hat{V} \equiv WH$$

这里面 $W$ 是一个经常性出现的patterns的字典(比如音乐中的鼓点)，而 $H$ 中的每一列 $h_n$ 表示每一个采样点 $v_n$ 中估测存在的patterns。我们可以把 $W$ 称为字典(dictionary)而 $H$ 成为激活矩阵(activation matrix)。同时我们也约定 $V$ 的维度是F $\times$ N。 $W$ 为 F $\times$ K，$H$ 为 K $\times$ N。

上面的式子中的因式分解在其他的领域里面也叫做字典学习(dictionary learning)低维估计(low-rank approximation)等等。最有名的方法是PCA，通过最小化$V$和$WH$的二次距离。别的方法有PCA的变体ICA，稀疏编码(sparse coding)，而NMF则用在非负的数据上，并限制$W$和$H$为非负矩阵。

NMF信号分解

下图是一个NMF工作的模式图，首先把音频转化为时频图，然后我们可以把他分解为特征字典和激活矩阵。

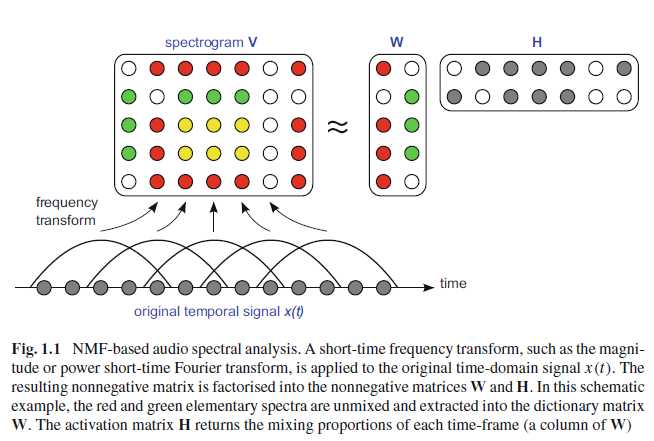
NMF 同样可以用在图像中，我们可以发现经过NMF分解，人脸可以分为各个部分（眼睛、鼻子、嘴巴），而PCA分解后的结果是特征脸(eigenfaces)。可以看出来，NMF一个很大的优势在于它的可解释性。

Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788.
https://www.nature.com/articles/44565

最优化问题NMF

NMF 的因式分解可以看作一个最小化问题

$$ \min_{W,H} D(V|WH) \text{ subject to } W \ge 0, H \ge 0$$

$$ D(V|WH) = \sum^F_{f=1}\sum^N_{N=1}d([V]{fn}|[WH]{fn}) $$

$ d(x|y) $ 是cost function，在别的应用中比较流行的选择是二次成本函数(quadratic cost function) $d_Q(x|y) = \frac{1}{2}(x-y)^2$。但它并不是很适合NMF。在音频信号处理应用中比较成功的cost function是 β-divergence。

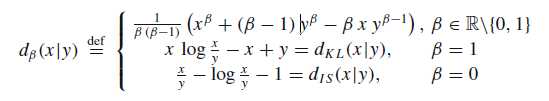
根据β-divergence导出的更新的公式如下：

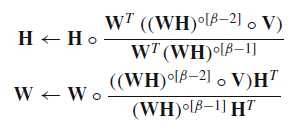
每次迭代，更新$ W $和$ H $。

总体的流程如下：

1. 输入一段音频，将音频通过短时傅里叶变换转化到时频谱（$V$）
2. 选择一个$W$$H$的共有维度K，初始化$W$和$H$，注意其中所有元素都要是非负的。
3. 使用上面的公式更新$W$和$H$。

NMF非负矩阵分解初探

标签：adr   att   obj   问题   tps   一个   特征   hat   learning   

原文地址：https://www.cnblogs.com/jinnsjj/p/9268459.html