标签:turn rate user new black leaves numbers OWIN lang
There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:
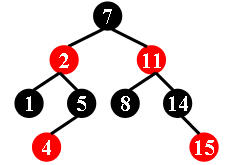
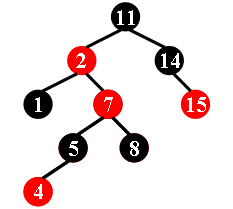
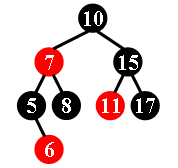
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.
 |  |  |
|---|---|---|
| Figure 1 | Figure 2 | Figure 3 |
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.
Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.
For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.
3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17
Yes No No
要求题目中写的很清楚,红黑树是二叉搜索树,所以给出前序遍历,那么中序遍历也可以知道(从小到大排序就是中序遍历),但负号不是代表大小,所以排序前,要取绝对值,然后建树,进行判断,按照题目要求,根结点必须是黑的(正的),
红色的儿子必须都是黑色,从某个点到所有的子孙叶子结点的路径包含黑色点个数相同。
代码:
#include <iostream> #include <cstdio> #include <cstring> #include <vector> #include <algorithm> using namespace std; struct tree { int data; tree *left,*right; }; int pre[31],in[31]; int k,n,flag; tree *build(int pre_l,int pre_r,int in_l,int in_r) { tree *t = new tree(); t -> left = t -> right = NULL; for(int i = in_l;i <= in_r;i ++) { if(in[i] == abs(pre[pre_l])) { if(i != in_l)t -> left = build(pre_l + 1,pre_l + i - in_l,in_l,i - 1); if(i != in_r)t -> right = build(pre_l + i - in_l + 1,pre_r,i + 1,in_r); break; } } t -> data = pre[pre_l]; return t; } int check(tree *t) { if(t == NULL)return 1; if(t -> data < 0 && (t -> left && t -> left -> data < 0 || t -> right && t -> right -> data < 0)) { flag = 0; return 0; } int d = check(t -> left),e = check(t -> right); if(d != e)flag = 0; return d + (t -> data > 0);///如果颜色为黑色,返回值加1 } void drop(tree *t) { if(t == NULL)return; drop(t -> left); drop(t -> right); delete t; } int main() { scanf("%d",&k); while(k --) { scanf("%d",&n); for(int i = 0;i < n;i ++) { scanf("%d",&pre[i]); in[i] = abs(pre[i]);///取绝对值 } flag = 1; sort(in,in + n); tree *head = build(0,n - 1,0,n - 1);///建树 if(head -> data < 0)flag = 0;///根结点不是黑色 else check(head);///检查是否满足 drop(head);///释放空间 puts(flag ? "Yes" : "No"); } }
1135 Is It A Red-Black Tree(30 分)
标签:turn rate user new black leaves numbers OWIN lang
原文地址:https://www.cnblogs.com/8023spz/p/9277873.html