码迷，mamicode.com
首页 > 其他好文 > 详细

模板整理

时间：2018-07-07 20:51:55      阅读：151      评论：0      收藏：0      [点我收藏+]

标签：n+1   路径压缩   最短路   前缀数组   center   style   树根   dfs   printf   

RT

有些代码写的时间很长了，会有一些错误或者非常XX的写法。。。还有很多算法不全。。。有空更新

P3385 【模板】负环

题目描述

暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索

输入输出格式

输入格式：

 

第一行一个正整数T表示数据组数，对于每组数据：

第一行两个正整数N M，表示图有N个顶点，M条边

接下来M行，每行三个整数a b w，表示a->b有一条权值为w的边（若w<0则为单向，否则双向）

 

输出格式：

 

共T行。对于每组数据，存在负环则输出一行"YE5"(不含引号)，否则输出一行"N0"(不含引号)。

 

输入输出样例

输入样例#1： 
 
2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8
输出样例#1： 
 
N0
YE5

说明

n\leq 2000n≤2000 m\leq 3000m≤3000-10000\leq w\leq 10000−10000≤w≤10000T\leq

code

#include<queue>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

using namespace std;

const int INF = 10000;
const int MAXN = 30000;
int T, n, m;
int head[MAXN * 2], tot = 0;
int dis[MAXN], cnt[MAXN];
bool vis[MAXN];

struct Edge {
    int node, next, value;
}e[MAXN];

inline int read() {
    int num = 0, f = 1; char ch = getchar();
    while (!isdigit(ch)) { if (ch == ‘-‘) f = -1; ch = getchar(); }
    while (isdigit(ch)) { num = num * 10 + ch - ‘0‘; ch = getchar(); }
    return num * f;
}

void Add_Edge(int x, int y, int w) {
    e[++tot].node = y; e[tot].value = w; e[tot].next = head[x]; head[x] = tot;
} 

bool SPFA(int s) {
    queue<int> q;
    memset(dis, INF, sizeof(dis));
    memset(vis, false, sizeof(vis));
    memset(cnt, 0, sizeof(cnt));
    dis[s] = 0;
    vis[s] = true;
    cnt[s] = 1;
    q.push(s);
    while (!q.empty()) {
        int h = q.front();
        q.pop();
        vis[h] = false;
        for (int i = head[h], v; ~i, v = e[i].node; i = e[i].next) {
            if (dis[h] + e[i].value < dis[v]) {
                if (++ cnt[v] >= n) return true;
                dis[v] = dis[h] + e[i].value;
                if (!vis[v]) {
                    q.push(v);
                    vis[v] = true;
                }
            }
        } 
    }
    return false;
}

int main() { 
    T = read();
    while (T --) {
        tot = 0;
        memset(head, -1, sizeof(head));
        n = read(); m = read();
        for (int i = 1; i <= m; ++ i) {
            int x = read(), y = read(), w = read();
            Add_Edge(x, y, w);
            if (w >= 0) Add_Edge(y, x, w);
        }
        if(SPFA(1)) printf("YE5\n");
        else printf("N0\n");
    }
    return 0;
}

P3387 【模板】缩点

题目背景

缩点+DP

题目描述

给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入输出格式

输入格式：

 

第一行，n,m

第二行，n个整数，依次代表点权

第三至m+2行，每行两个整数u,v，表示u->v有一条有向边

 

输出格式：

 

共一行，最大的点权之和。

 

输入输出样例

输入样例#1： 
 
2 2
1 1
1 2
2 1
输出样例#1： 
 
2

说明

n<=10^4,m<=10^5,点权<=1000

算法：Tarjan缩点+DAGdp

code

某同学的毒瘤代码

#include <algorithm>
#include <cstdio>
#include <cstring>

const int Max = (int)1e9 + 7;
const int MaxnEdge = (int)1e5 + 5;
const int MaxnVertex = (int)1e4 + 5;

int Cnt,MergeCnt;
int Head[MaxnVertex],MergeHead[MaxnVertex];
struct Graph{
    int Vertex;
    int Next;
}Edge[MaxnEdge],MergeEdge[MaxnVertex];
int VertexN[MaxnVertex],MergeVertexN[MaxnVertex];

int DFSN[MaxnVertex],Lowest[MaxnVertex];
int Top,Stack[MaxnVertex];
bool InStack[MaxnVertex];
int Time;

bool IsNotZero[MaxnVertex];
int Link[MaxnEdge];
int MergeVertex;

int H,T;
int Queue[MaxnVertex];
bool Visited[MaxnVertex];
int Dis[MaxnVertex];

int Ans;

int N,M;

void Insert(int From,int To,int &TmpCnt,int *TmpHead,Graph *TmpEdge){
    TmpEdge[++ TmpCnt].Next = TmpHead[From];
    TmpEdge[TmpCnt].Vertex = To;
    TmpHead[From] = TmpCnt;
}

void Tarjan(int X){
    DFSN[X] = Lowest[X] = ++Time;
    Stack[++ Top] = X;
    InStack[X] = true;

    int TmpV; // TmpVertex
    for(int i = Head[X];i;i = Edge[i].Next){
        TmpV = Edge[i].Vertex;
        if(InStack[TmpV]) Lowest[X] = std::min(Lowest[X], DFSN[TmpV]);
        else if (!DFSN[TmpV]) Tarjan(TmpV), Lowest[X] = std::min(Lowest[X], Lowest[TmpV]); 
        /*if(!DFSN[TmpV]){
            Tarjan(TmpV);
            Lowest[X] = std::min(Lowest[X],Lowest[TmpV]);
        } else if(InStack[TmpV])
            Lowest[X] = std::min(Lowest[X],Lowest[TmpV]);*/
    }
    /*if(DFSN[X] == Lowest[X]){
        ++ MergeVertex;
        TmpV = Stack[-- Top];
        while(TmpV != X){
            Link[TmpV] = MergeVertex;
            InStack[TmpV] = false;
            MergeVertexN[MergeVertex] += VertexN[TmpV];
            TmpV = Stack[-- Top];
        }
    }*/
    if(DFSN[X] == Lowest[X]){
        ++ MergeVertex;
        TmpV = Stack[Top];
        while(TmpV != X){
            Link[TmpV] = MergeVertex;
            InStack[TmpV] = false;
            MergeVertexN[MergeVertex] += VertexN[TmpV];
            TmpV = Stack[-- Top];
        }
        Link[TmpV] = MergeVertex;
        InStack[TmpV] = false;
        MergeVertexN[MergeVertex] += VertexN[TmpV];
        TmpV = Stack[-- Top];
    }
}

void Merge(){
    int TmpV; //TmpVertex
    for(int i = 1;i <= N;++ i){
        for(int j = Head[i];j;j = Edge[j].Next){
            TmpV = Edge[j].Vertex;
            if(Link[TmpV] != Link[i]){
                IsNotZero[Link[TmpV]] = true;
                Insert(Link[i],Link[TmpV],MergeCnt,MergeHead,MergeEdge);
            }
        }
    }
}

void SPFA(int X){
    memset(Queue,0,sizeof(Queue));
    memset(Dis,0,sizeof(Dis));
    memset(Visited,0,sizeof(Visited));
    H = T = 0;
    Queue[++ T] = X;
    Visited[X] = true;
    Dis[X] = MergeVertexN[X];
    int TmpV,TmpVT,TmpSum; //TmpVertex,TmpVerteTo
    while(H != T){
        H = (H + 1) % MaxnVertex;
        TmpV = Queue[H];
        Visited[TmpV] = false;
        for(int i = MergeHead[TmpV];i;i = MergeEdge[i].Next){
            TmpVT = MergeEdge[i].Vertex;
            TmpSum = Dis[TmpV] + MergeVertexN[TmpVT];
            if(Dis[TmpVT] < TmpSum){
                Dis[TmpVT] = TmpSum;
                if(!Visited[TmpVT]){
                    T = (T + 1) % MaxnVertex;
                    Queue[T] = TmpVT;
                    Visited[TmpVT] = true;
                }
            }
        }
    }
    for(int i = 1;i <= N;++ i)
    //for(int i = 1;i <= MergeVertex;++ i)
        Ans = std::max(Ans,Dis[i]);
        
}

void Read(){
    scanf("%d%d",&N,&M);
    for(int i = 1;i <= N;++ i)
        scanf("%d",&VertexN[i]);
    int TmpX,TmpY;
    for(int i = 1;i <= M;++ i){
        scanf("%d%d",&TmpX,&TmpY);
        Insert(TmpX,TmpY,Cnt,Head,Edge);
    }
}

int main(){
    Read();
    for(int i = 1;i <= N;++ i)
        if(!DFSN[i])
            Tarjan(i);
    Merge();
    for(int i = 1;i <= MergeVertex;++ i)
        if(!IsNotZero[i])
            SPFA(i);
    printf("%d",Ans);
    return 0;
}

 

mine

#include<queue>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

using namespace std;

const int MAXN = 100010;

int n,m,x,y,ans;
int tot,head[MAXN]; 
int bc; 
int cnt; 
int top;
int dfn[MAXN]; 
int low[MAXN]; 
int num[MAXN]; 
int col[MAXN];
int vis[MAXN];
int stack[MAXN];
int a[MAXN];
int dis[MAXN];
int linkx[MAXN], linky[MAXN];

struct Edge {
    int node,next,value;
}e[MAXN];

inline int read() {
    int num = 0, f = 1; char ch = getchar();
    while (!isdigit(ch)) { if (ch == ‘-‘) f = -1; ch = getchar(); }
    while (isdigit(ch)) { num = num * 10 + ch - ‘0‘; ch = getchar(); }
    return num * f; 
}

void Add_Edge(int x,int y) {
    e[++tot].next = head[x]; e[tot].node = y; head[x] = tot;
}

void tarjan(int x) {
    dfn[x] = low[x] = ++cnt;
    stack[++top] = x; 
    vis[x] = 1;
    for (int i = head[x],v; v = e[i].node,i; i = e[i].next) {
        if (vis[v]) low[x] = min(low[x], dfn[v]);
        else if (!dfn[v]) tarjan(v), low[x] = min(low[x], low[v]);
    }
    if (low[x] == dfn[x]) {
        ++bc; 
        vis[x] = 0;
        while (stack[top+1] != x) {
            col[stack[top]] = bc; 
            num[bc] += a[stack[top]];
            vis[stack[top]] = 0;
            top--;
         }
    }
}

void SPFA(int x) {
    memset(dis, 0, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    queue<int> que;
    dis[x] = num[x];
    vis[x] = 1;
    que.push(x);
    while (!que.empty()) {
        int h = que.front();
        vis[h] = 0;
        que.pop();
        for (int i = head[h]; i ; i = e[i].next) {
            int v = e[i].node;
            if (dis[v] < dis[h] + num[v]) {
                dis[v] = dis[h] + num[v];
                if (!vis[v]) { vis[v] = 1; que.push(v); }
            }
        }
    } 
    for (int i = 1; i <= bc; ++ i) ans = max(ans, dis[i]);
}

int main() {
    n = read(); m = read();
    for (int i = 1; i <= n; ++ i) a[i] = read();
    for (int i = 1; i <= m; ++ i) {
        x = read(); y = read();
        Add_Edge(x,y);
        linkx[i] = x; linky[i] = y;
    }
    for (int i = 1; i <= n; ++ i) if (!dfn[i]) tarjan(i);
    memset(head, 0, sizeof(head));
    memset(e, 0, sizeof(e));
    for (int i = 1; i <= m; ++ i) 
        if (col[linkx[i]] != col[linky[i]]) Add_Edge(col[linkx[i]], col[linky[i]]);
    for (int i = 1; i <= bc; ++ i) SPFA(i);
    cout << ans << endl;
    return 0;
}

并差集

//_查询
//路径压缩
int find(int i) {
    if (fa[i] != i) fa[i] = find(fa[i]);
    return fa[i];
}

//简单合并
bool unionSet(int far, int son) {
    int a = find(far);
    int b = find(son);
    if (a == b) return false;
    fa[b] = a;
    cnt[a] += cnt[b];
    return true;
}
 
//_按秩合并
//没怎么用过，一般路径压缩就够了。copy by 某大佬
int rank[N] = {0};
bool _unionSet(int x, int y) {
    int a = find(x);
    int b = find(y);
    if (a == b) return false;
    if (rank[a] > rank[b]) {
        fa[b] = a; 
        cnt[a] += cnt[b];
    }
    else {
        fa[a] = b; 
        cnt[b] += cnt[a];
        if (rank[a] == rank[b])
            rank[b]++; 
    }
    return true;
}

乘法逆元

typedef long long ll;

void exgcd(ll a, ll b, ll& d, ll& x, ll& y) {
    if (! b) { d = a; x = 1; y = 0; }
    else { exgcd(b, a % b, d, y, x); y -= x * (a / b); }
}

ll inv(ll a, ll p) {
    ll d, x, y;
    exgcd(a, p, d, x, y);
    return d == 1 ? (x + p) % p : -1;
}

P3388 【模板】割点（割顶）

题目背景

割点

题目描述

给出一个n个点，m条边的无向图，求图的割点。

输入输出格式

输入格式：

第一行输入n,m

下面m行每行输入x,y表示x到y有一条边

输出格式：

第一行输出割点个数

第二行按照节点编号从小到大输出节点，用空格隔开

输入输出样例

输入样例#1： 
 
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6
输出样例#1： 
 
1 
5

说明

n,m均为100000

tarjan 图不一定联通！！！

code

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#define MAXN 200010

using namespace std;

int n,m,cnt,head[MAXN],dfn[MAXN],low[MAXN],stack[MAXN],top,num,nums,ID,ans;
bool vis[MAXN],poi[MAXN],cut[MAXN];

struct Edge {
    int next,node,value;
}e[MAXN];

void add(int u,int v) {
    e[++cnt].node = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

void tarjan(int x,int father) {
    int son = 0;
    dfn[x] = low[x] = ++ID;
    for (int i = head[x] , v ; v = e[i].node , i ; i = e[i].next) {
        if (!dfn[v]) {
            tarjan(v,father);
            low[x] = min(low[x],low[v]);
            if (low[v] >= dfn[x] && x != father) cut[x] = true;
            else if (x == father) son++;
        }
        low[x] = min(low[x],dfn[v]);
    }
    if (x == father && son >= 2) cut[father] = true;  
}

int main() {
    scanf("%d%d",&n,&m);
    while (m--) {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    for (int i = 1; i <= n; i++) 
        if (!dfn[i]) tarjan(i,i);
    for (int i = 1; i <= n; i++) 
        if (cut[i]) ans++;
    printf("%d\n",ans);
    for (int i = 1; i <= n; i++)
        if (cut[i]) printf("%d ",i);
    return 0;
}

P3384 【模板】树链剖分

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1： 格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2： 格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3： 格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4： 格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

 

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

 

输出格式：

 

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

 

输入输出样例

输入样例#1： 
 
5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出样例#1： 
 
2
21

说明

时空限制：1s，128M

数据规模：

对于30%的数据： N \leq 10, M \leq 10N≤10,M≤10

对于70%的数据： N \leq {10}^3, M \leq {10}^3N≤103,M≤103

对于100%的数据： N \leq {10}^5, M \leq {10}^5N≤105,M≤105

code

不太会了已经QwQ

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
 
using namespace std;

const int MAXN = 2 * 1e6 + 10;
int cnt = 0, head[MAXN * 2];
int n, m, root, MOD, tim = 0, a[MAXN], b[MAXN];
int dep[MAXN], fat[MAXN], son[MAXN], tot[MAXN], top[MAXN], idx[MAXN];

struct Edge {
    int node, next;
}e[MAXN];

struct Tree {
    int lef, rig, wei, siz, tag;
}t[MAXN];

inline int read() {
    int num = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == ‘-‘) f = -1; 
        ch = getchar();
    }
    while (isdigit(ch)) {
        num = num * 10 + ch - ‘0‘;
        ch = getchar();
    } return num * f;
}

void add_edge(int x, int y) {
    e[++cnt].next = head[x]; head[x] = cnt; e[cnt].node = y; 
    e[++cnt].next = head[y]; head[y] = cnt; e[cnt].node = x; 
}

void update(int u) {
    t[u].wei = (t[u << 1].wei + t[u << 1 | 1].wei + MOD) % MOD;
}

void build(int u, int l, int r) {
    int lu = u << 1, ru = u << 1 | 1, mid = (l + r) >> 1;
    t[u].lef = l; t[u].rig = r; t[u].siz = r - l + 1;
    if (l == r) {
        t[u].wei = a[l];
        return ;
    }
    build(lu, l, mid); build(ru, mid + 1, r);
    update(u);
}

int dfs1(int now, int fa, int de) {
    dep[now] = de;
    fat[now] = fa;
    tot[now] = 1;
    int maxson = -1;
    for (int i = head[now]; i ; i = e[i].next) {
        if (e[i].node == fa) continue;
        tot[now] += dfs1(e[i].node, now, de + 1);
        if (tot[e[i].node] > maxson)
            maxson = tot[e[i].node], son[now] = e[i].node; 
    }
    return tot[now];
}

void dfs2(int now, int topf) {
    idx[now] = ++tim;
    a[tim] = b[now];
    top[now] = topf;
    if (!son[now]) return ;
    dfs2(son[now], topf);
    for (int i = head[now]; i ; i = e[i].next)
        if (!idx[e[i].node])
            dfs2(e[i].node, e[i].node); 
}

void pushdown(int u) {
    int lu = u << 1, ru = u << 1 | 1;
    if (!t[u].tag) return ;
    t[lu].wei = (t[lu].wei + t[lu].siz * t[u].tag) % MOD;
    t[ru].wei = (t[ru].wei + t[ru].siz * t[u].tag) % MOD;
    t[lu].tag = (t[lu].tag + t[u].tag) % MOD;
    t[ru].tag = (t[ru].tag + t[u].tag) % MOD;
    t[u].tag = 0;
}

void IntervalAdd(int u, int l, int r, int v) {
    int lu = u << 1, ru = u << 1 | 1, mid = (t[u].lef + t[u].rig) >> 1;
    if (l <= t[u].lef && t[u].rig <= r) {
        t[u].wei += t[u].siz * v;
        t[u].tag += v;
        return ; 
    }
    pushdown(u);
    if (l <= mid) IntervalAdd(lu, l, r, v);
    if (r > mid)  IntervalAdd(ru, l, r, v);
    update(u);
}

void TreeAdd(int x, int y, int v) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        IntervalAdd(1, idx[top[x]], idx[x], v);
        x = fat[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    IntervalAdd(1, idx[x], idx[y], v);
} 

int IntervalSum(int u, int l, int r) {
    int ans = 0, lu = u << 1, ru = u << 1 | 1, mid = (t[u].lef + t[u].rig) >> 1;
    if (l <= t[u].lef && t[u].rig <= r) return t[u].wei;
    pushdown(u);
    if (l <= mid) ans = (ans + IntervalSum(lu, l, r)) % MOD;
    if (r > mid)  ans = (ans + IntervalSum(ru, l, r)) % MOD;
    return ans;
}

void TreeSum(int x, int y) {
    int ans = 0;
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        ans = (ans + IntervalSum(1, idx[top[x]], idx[x])) % MOD;
        x = fat[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    ans = (ans + IntervalSum(1, idx[x], idx[y])) % MOD;
    printf("%d\n", ans);
}

int main() {
    memset(head, 0, sizeof (head));
    n = read(); m = read(); root = read(); MOD = read();
    for (int i = 1; i <= n; i++) b[i] = read();
    for (int i = 1; i <= n - 1; i++) {
        int x = read(), y = read();
        add_edge(x, y);
    }
    dfs1(root, 0, 1); dfs2(root, root);
    build(1, 1, n);
    while (m--) {
        int x, y, z, kind = read();
        if (kind == 1) {
            x = read(); y = read(); z = read(); z = z % MOD;
            TreeAdd(x, y, z);
        }
        else if (kind == 2) {
            x = read(); y = read();
            TreeSum(x, y);
        }
        else if (kind == 3) {
            x = read(); z = read();
            IntervalAdd(1, idx[x], idx[x] + tot[x] - 1, z % MOD);
        }
        else if (kind == 4) {
            x = read();
            printf("%d\n", IntervalSum(1, idx[x], idx[x] + tot[x] - 1));
        }
    }
    return 0;
}

P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

 

输出格式：

 

输出包含若干行整数，即为所有操作2的结果。

 

输入输出样例

输入样例#1： 
 
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出样例#1： 
 
14
16

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

code

#include<iostream>
#include<cstdio>
#define INT register int 

using namespace std;

const int MAXN = 5e5 + 5;
int n, m, a[MAXN];
char ss[1<<17], *A = ss, *B = ss;

char sr[20], z[20]; 
int C = -1, Z;

inline void updata(int pos,int x) { 
    while (pos <= n) { 
        a[pos] += x; 
        pos += (-pos) & pos; 
    } 
}

inline int query(int pos) { 
    int ans = 0; 
    while(pos) { 
        ans += a[pos]; 
        pos -= (-pos) & pos;
    } 
    return ans;
}

int main(){
    scanf("%d%d", &n, &m);
    for (INT i = 1; i <= n; ++ i) {
        int x; 
        scanf("%d", &x);
        updata(i, x);
    }
    for (INT i = 1; i <= m; ++ i) {
        int opt, l, r;
        scanf("%d%d%d", &opt, &l, &r);
        if (opt == 1) updata(l, r);
        else printf("%d\n", query(r) - query(l - 1));
    }
    return 0;
}

P3390 【模板】矩阵快速幂

题目背景

矩阵快速幂

题目描述

给定n*n的矩阵A，求A^k

输入输出格式

输入格式：

 

第一行，n,k

第2至n+1行，每行n个数，第i+1行第j个数表示矩阵第i行第j列的元素

 

输出格式：

 

输出A^k

共n行，每行n个数，第i行第j个数表示矩阵第i行第j列的元素，每个元素模10^9+7

 

输入输出样例

输入样例#1： 
 
2 1
1 1
1 1
输出样例#1： 
 
1 1
1 1

说明

n<=100, k<=10^12, |矩阵元素|<=1000 算法：矩阵快速幂

code

#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long LL;

const LL mod=1000000007;

int n; LL m;

struct Matrix {
    LL a[105][105];
    Matrix operator * (const Matrix &x) const {
        Matrix res;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++) {
                res.a[i][j] = 0;
                for (int k = 1; k <= n; k++)
                    res.a[i][j] = (res.a[i][j] + a[i][k] * x.a[k][j]) % mod;
            }
        return res;
    }
}x,ans;

int main() {
    scanf("%d%lld",&n,&m);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            scanf("%lld",&x.a[i][j]);
    ans = x, m--;
    while (m) {
        while ((m & 1LL) == 0) 
            x = x * x,m >>= 1LL;
        ans = ans * x; m >>= 1LL; x = x * x; 
    }
    for (int i = 1; i <= n; i++) {
        printf("%lld",ans.a[i][1]);
        for (int j = 2; j <= n; j++)
            printf(" %lld",ans.a[i][j]);
        printf("\n");
    }
    return 0;
}

P3382 【模板】三分法

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

 

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

 

输出格式：

 

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

 

输入输出样例

输入样例#1： 
 
3 -0.9981 0.5
1 -3 -3 1
输出样例#1： 
 
-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

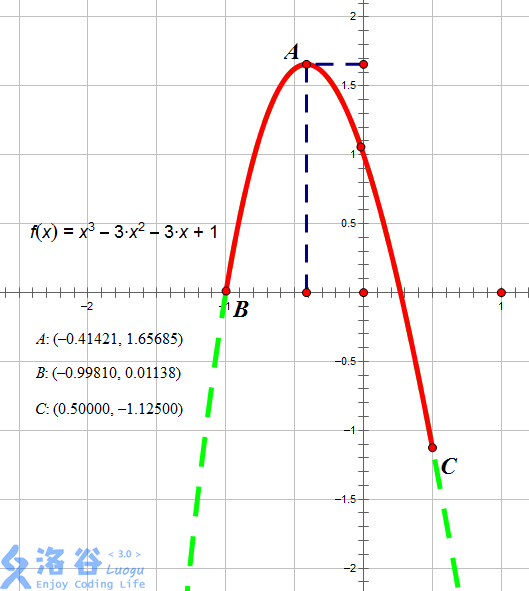
技术分享图片

如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

（Tip.l&r的范围并不是非常大ww不会超过一位数）

code

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

const int MAXN = 15;
int n;
double a[MAXN];

double F(double x) {
    double Sum = 0;
    for (int i = n; i >= 0; -- i) Sum = Sum * x + a[i];
    return Sum;
}

int main() {
    double L, R;
    cin >> n >> L >> R;
    for (int i = n; i >= 0; -- i) cin >> a[i];
    for (int i = 0; i < 100; ++ i) {
        double m1 = L + (R - L) / 3.0;
        double m2 = R - (R - L) / 3.0;
        if (F(m1) > F(m2)) R = m2; 
        else L = m1;
    }
    printf("%.5lf\n", L);
    return 0;
}

P3386 【模板】二分图匹配

题目背景

二分图

感谢@一扶苏一 提供的hack数据 （没错这就是ZAY大佬）

题目描述

给定一个二分图，结点个数分别为n,m，边数为e，求二分图最大匹配数

输入输出格式

输入格式：

 

第一行，n,m,e

第二至e+1行，每行两个正整数u,v，表示u,v有一条连边

 

输出格式：

 

共一行，二分图最大匹配

 

输入输出样例

输入样例#1： 
 
1 1 1
1 1
输出样例#1： 
 
1

说明

n,m \leq 1000n,m≤1000 ， 1 \leq u \leq n1≤u≤n ， 1 \leq v \leq m1≤v≤m

因为数据有坑，可能会遇到 v>mv>m 的情况。请把 v>mv>m 的数据自觉过滤掉。

算法：二分图匹配

code

匈牙利

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

const int N = 1e3;
bool f[N][N], vis[N];
int n, m, e, match[N];

inline int read() {
    int num = 0, f = 1; char ch = getchar();
    while (ch < ‘0‘ || ch > ‘9‘) { if (ch == ‘-‘) f = -1; ch = getchar(); }
    while (ch >= ‘0‘ && ch <= ‘9‘) { num = num * 10 + ch - ‘0‘; ch = getchar(); }
    return num * f;
}

bool dfs(int pos) {
    for (int i = 1; i <= m; ++ i) {
        if (f[pos][i] && !vis[i]) {
            vis[i] = true;
            if (!match[i] || dfs(match[i])) {
            /*如果这个点i还未匹配则pos和他匹配，如果这个点已经匹配，
            那么如果本来和他匹配的点match[i]还能找到另一个点匹配则pos把i“抢”过来，
            让match[i]去匹配另一个点，否则就不干涉i和match[i]匹配*/
                match[i] = pos;
                return true;
            }
        }
    }
    return false;
}

int main() {
    n = read(); m = read(); e = read();
    for (int i = 1; i <= e; ++ i) {
        int x = read(), y = read();
        if (x <= n && y <= m) f[x][y] = true;
    }
    int ans = 0;
    for (int i = 1; i <= n; ++ i) {
        memset(vis, 0, sizeof(vis));
        if (dfs(i)) ans++;
    }
    printf("%d\n", ans);
}

DINIC

(脑子一抽写成了class QwQ。。。懒得改了）

#pragma GCC optimize("O8")
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

const int N = 2010;
const int M = 1000010;
const int INF = 0x7fffffff;

class MAXFLOW {
    public:        
        void init() {
            int n1 = read(), n2 = read(), m0 = read(); m = 0;
            n = n1 + n2 + 2;
            for (int i = 1; i <= m0; ++ i) {
                int x = read(), y = read();
                if (x <= n1 && y <= n2) {
                    Add_Edge(x + 1, y + n1 + 1, 1, m + 2);
                    Add_Edge(y + n1 + 1, x + 1, 0, m);
                }
            }
            for (int i = 1; i <= n1; ++ i) {
                Add_Edge(1,i + 1, 1, m + 2);
                Add_Edge(i + 1, 1, 0, m);
            }
            for (int i = 1; i <= n2; ++ i) {
                Add_Edge(i + n1 + 1, n, 1, m + 2);
                Add_Edge(n, i + n1 + 1, 0, m);
            }
            s = 1; t = n;
        }
        
        void doit() {
            printf("%d\n",DINIC());
        }
        
        bool bfs() {
            while (!que.empty()) que.pop();
            memset(dep, 0, sizeof(dep));
            que.push(s);
            dep[s] = 1;
            while (!que.empty()) {
                int h = que.front(); 
                que.pop();
                for (int i = head[h], v; i, v = e[i].node; i = e[i].next) {
                    if (e[i].value > 0 && !dep[v]) {
                        dep[v] = dep[h] + 1;
                        que.push(v);
                    }
                }
            }
            if (dep[t]) return true;
            return false;
        }

        int dfs(int pos, int cur) {
            if (pos == t) return cur;
            int rst = cur;
            for (int i = head[pos], v; i, v = e[i].node; i = e[i].next) {
                if (dep[v] == dep[pos] + 1 && e[i].value > 0 && rst) {
                    int flow = dfs(v, std::min(e[i].value, rst));
                    if (flow > 0) {
                        e[i].value -= flow;
                        rst -= flow;
                        e[e[i].rev].value += flow;
                    }
                }
            }
            return cur - rst;
        }

        int DINIC() {
            int ans = 0;
            while (bfs()) ans += dfs(s, INF);
            return ans;
        }
        
    private:
        int n, m, s, t, dep[N], head[N];
        std::queue<int> que;
        
        struct Edge {
            int node,value,next,rev;
        } e[M<<1];
        
        inline int read() {
            int num = 0, f = 1; char ch = getchar();
            while (ch < ‘0‘ || ch > ‘9‘) { if (ch == ‘-‘) f = -1; ch = getchar(); }
            while (ch >= ‘0‘ && ch <= ‘9‘) { num = (num << 3) + (num << 1) + (ch ^ 48); ch = getchar(); }
            return num * f;
        }
        
        inline void Add_Edge(int x,int y,int v,int rev) {
            e[++m].node = y; e[m].value = v; e[m].rev = rev; 
            e[m].next = head[x]; head[x] = m;
        }
} Maxflow;

int main() {
    Maxflow.init();
    Maxflow.doit();
    return 0;
}

P3375 【模板】KMP字符串匹配

题目描述

如题，给出两个字符串s1和s2，其中s2为s1的子串，求出s2在s1中所有出现的位置。

为了减少骗分的情况，接下来还要输出子串的前缀数组next。

（如果你不知道这是什么意思也不要问，去百度搜[kmp算法]学习一下就知道了。）

输入输出格式

输入格式：

 

第一行为一个字符串，即为s1

第二行为一个字符串，即为s2

 

输出格式：

 

若干行，每行包含一个整数，表示s2在s1中出现的位置

接下来1行，包括length(s2)个整数，表示前缀数组next[i]的值。

 

输入输出样例

输入样例#1： 
 
ABABABC
ABA
输出样例#1： 
 
1
3
0 0 1

说明

时空限制：1000ms,128M

数据规模：

设s1长度为N，s2长度为M

对于30%的数据：N<=15，M<=5

对于70%的数据：N<=10000，M<=100

对于100%的数据：N<=1000000，M<=1000000

样例说明：

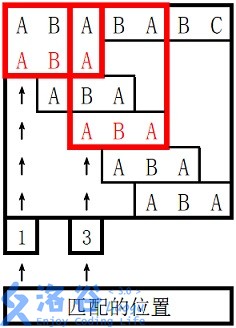
技术分享图片

所以两个匹配位置为1和3，输出1、3

code

#include<cstdio> 
#include<cstring>

using namespace std;

char a1[2000000],a2[2000000];
int kmp[2000000];

int main() {
    scanf("%s%s",&a1,&a2);
    int len1 = strlen(a1);
    int len2 = strlen(a2);
    kmp[0] = kmp[1] = 0;
    int k = 0;
    for (int i = 1; i <= len2; i++) {
        while (k && a2[i] != a2[k])
            k = kmp[k];
        kmp[i + 1] = a2[i] == a2[k] ? ++ k : 0;
    }
    k = 0;
    for (int i = 0; i < len1; i++) {
        while (k && a1[i] != a2[k]) 
            k = kmp[k];
        k += a1[i] == a2[k] ? 1 : 0;
        if (k == len2)
            printf("%d\n",i - len2 + 2); 
    }
    for (int i = 1; i <= len2; i++)
        printf("%d ",kmp[i]);
    return 0;
}

P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

 

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

 

输出格式：

 

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

 

输入输出样例

输入样例#1： 
 
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出样例#1： 
 
4
4
1
4
4

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

技术分享图片

第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

code

#include<cstdio>
#include<iostream>

using namespace std;

const int MAXN = 100010;

int n,m,tot,x,y,a,b,s;
int father[MAXN][20];
int dep[MAXN],head[MAXN];

struct edge {
    int next; 
    int node;
    int value;
}Edge[MAXN];

inline int read() {
    int num = 0 , f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == ‘-‘) f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        num = num * 10 + ch - ‘0‘;
        ch = getchar(); 
    } 
    return num * f;
}

inline void add(int x,int y) { 
    Edge[++tot].node = x; Edge[tot].next = head[y]; head[y] = tot;
    Edge[++tot].node = y; Edge[tot].next = head[x]; head[x] = tot;
}

inline void build(int s) {
    for (int i = head[s]; i ; i = Edge[i].next) {
        int v = Edge[i].node;
        if (!dep[v]) {
            dep[v] = dep[s] + 1;    
            father[v][0] = s;
            build(v);
        }
    }
}

int LCA(int x,int y) {
    if (dep[x] < dep[y])
        swap(x,y);
    for (int i = 19; i >= 0; i--)
        if (dep[father[x][i]] >= dep[y])
            x = father[x][i];
    if (x == y) return y;
    for (int i = 19; i >= 0; i--)
        if (father[x][i] != father[y][i]) {
            x = father[x][i];
            y = father[y][i];
        }
    return father[x][0];
}

int main() {
    n = read(); m = read(); s = read();
    for(int i = 1; i <= n - 1; i++) {
        x = read(); y = read();
        add(x,y);
    }
    dep[s] = 1; build(s); 
    for (int j = 1; j <= 19; j++)    
        for (int i = 1; i <= n; i++)
            father[i][j] = father[father[i][j - 1]][j - 1];
    for (int i = 1; i <= m; i++){
        a = read(); b = read();
        printf("%d\n",LCA(a,b));
    }
    return 0;
}

P3371 【模板】单源最短路径

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

 

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

 

输出格式：

 

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

 

输入输出样例

输入样例#1： 
 
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出样例#1： 
 
0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

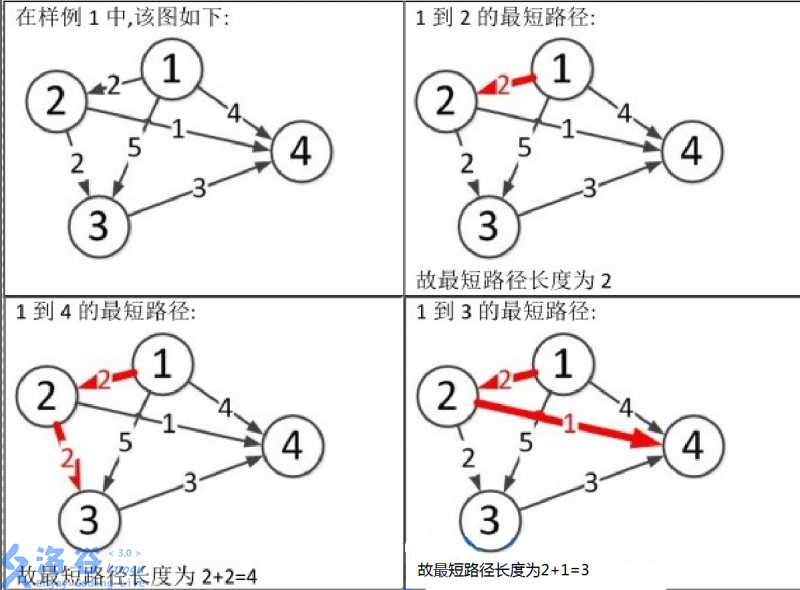
技术分享图片

图片1到3和1到4的文字位置调换

code

Dijkstra

#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

const int MAXN = 10010;
const int MAXM = 500010;
const int maxx = 2147483647;

int n,m,s,x,y,z,cnt,h,v;
int head[MAXN],d[MAXN];
bool vis[MAXN];

queue <int>q;

struct edge{
    int next;
    int node;
    int value;
}Edge[MAXM];

void add(int u,int v,int w) {
    Edge[++cnt].next = head[u];
    Edge[cnt].node = v;
    Edge[cnt].value = w;
    head[u] = cnt;
}

void SPFA() {
    while (!q.empty()) q.pop();
    memset(vis,0,sizeof(vis)); 
    q.push(s);
    d[s] = 0; 
    vis[s] = true;
    while (!q.empty()) {
        h = q.front() ;
        q.pop() ;
        vis[h] = 0;
        for (int i = head[h]; i ; i = Edge[i].next) {
            v = Edge[i].node;
            if (d[h] + Edge[i].value < d[v]) {
                d[v] = d[h] + Edge[i].value;
                if (!vis[v]) {
                    q.push(v);
                    vis[v] = true;
                }
            }
        }
    } 
}

int main() {
    scanf("%d%d%d",&n,&m,&s);
    for (int i = 1; i <= n; i++)
        d[i] = maxx;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    SPFA();
    for (int i = 1; i <= n; i++) 
        printf("%d ",d[i]);
    return 0;
}

SPFA

 

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<iostream>
#define MAXN 500010
#define oo 2147483647

using namespace std;

int head[MAXN * 2],dis[MAXN],tot,n,m,s;
bool vis[MAXN];

typedef pair<int, int> pir;

struct Edge {
    int node;
    int next;
    int value;
}e[MAXN];

inline void add(int x,int y,int z) {
    e[++tot].node = y; e[tot].value = z; e[tot].next = head[x]; head[x] = tot;
}

priority_queue<pir, vector<pir>, greater<pir> > que;

void dijkstra(int s) {
    dis[s] = 0;
    que.push(make_pair(dis[s], s));
    while (!que.empty()) {
        pir temp = que.top();
        que.pop();
        int x = temp.second;
        if (!vis[x]) {
            vis[x] = true;
            for (int i = head[x]; i ; i = e[i].next) {
                int v = e[i].node;
                if (dis[v] > dis[x] + e[i].value) {
                    dis[v] = dis[x] + e[i].value;
                    que.push(make_pair(dis[v],v));
                }
            }
        }
    }
}

inline int read() {
    int num = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == ‘-‘) f = -1;
        ch = getchar(); 
    }
    while (isdigit(ch)) {
        num = num * 10 + ch - ‘0‘;
        ch = getchar();
    }
    return num * f;
}

int main() {
    n = read(); m = read(); s = read();
    for (int i = 1; i <= m; i++) {
        int x,y,z;
        x = read(); y = read(); z = read();
        add(x,y,z);
    }
    for (int i = 1; i <= n; i++) dis[i] = oo;
    dijkstra(s);
    for (int i = 1; i <= n; i++)
        printf("%d ",dis[i]);
    return 0;
}

 

P3389 【模板】高斯消元法

题目背景

Gauss消元

题目描述

给定一个线性方程组，对其求解

输入输出格式

输入格式：

 

第一行，一个正整数 nn

第二至 n+1n+1 行，每行 n+1n+1 个整数，为 a_1, a_2 \cdots a_na1?,a2??an? 和 bb ，代表一组方程。

 

输出格式：

 

共n行，每行一个数，第 ii 行为 x_ixi? （保留2位小数）

如果不存在唯一解，在第一行输出"No Solution".

 

输入输出样例

输入样例#1： 
 
3
1 3 4 5
1 4 7 3
9 3 2 2
输出样例#1： 
 
-0.97
5.18
-2.39

说明

1 \leq n \leq 100, \left | a_i \right| \leq {10}^4 , \left |b \right| \leq {10}^41≤n≤100,∣ai?∣≤104,∣b∣≤104

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

class Gussian {
    public:
        void init() {
            n = read();
            for (int i = 1; i <= n; ++ i)
                for (int j = 1; j <= n + 1; ++ j)
                    a[i][j] = read();
        }
        
        void doit() {
            for (int i = 1; i <= n; ++ i) {
                int k = i; double t;
                for (int j = i + 1; j <= n; ++ j) 
                       if (Abs(a[k][i]) < Abs(a[j][i])) k = j;
                if (k != i) for (int j = 1; j <= n + 1; ++ j)
                t = a[k][j], a[k][j] = a[i][j], a[i][j] = t;
             if (Abs(a[i][i]) >= eps)
                    for (int j = 1; j <= n; ++ j) { 
                        if (i != j) {
                            t = a[j][i] / a[i][i];
                            for (int k = 1; k <= n + 1; ++ k)
                                a[j][k] -= t * a[i][k];
                        }
                    }
            }
            int wq = 0, wj = 0;
            for (int i = 1; i <= n; ++ i) {
                int j = 1;
                while (Abs(a[i][j]) < eps && j <= n + 1) ++ j;
                if (j > n + 1) wq = 1;
                if (j == n + 1) wj = 1; 
            }
            if (wj) { printf("No Solution"); flag = true; return ; }
            if (wq) { printf("No Solution"); flag = true; return ; }
            for (int i = n; i >= 1; -- i) {
                for (int k = i + 1; k <= n; ++ k)
                    a[i][n+1] -= a[i][k] * f[k];
                f[i] = a[i][n+1] / a[i][i];
            }
        }
        
        void print() {
            if (!flag) for (int i = 1; i <= n; ++ i) 
                printf("%.2lf\n", f[i]);
        }
        
    private:
        const double eps = 1e-5;
        double a[101][101],f[101] = {0};
        int n;
        bool flag = false;
        
        inline int read() {
            int num = 0, f = 1; char ch = getchar();
            while (!isdigit(ch)) { if (ch == ‘-‘) f = -1; ch = getchar(); }
            while (isdigit(ch)) { num = num * 10 + ch - ‘0‘; ch = getchar(); } 
            return num * f;
        }
        
        double Abs(double num) { return num < 0 ? - num : num; }
        
}gussian; 

int main() {
    gussian.init();
    gussian.doit();
    gussian.print();
}

中国剩余定理

LL ex_gcd(LL a,LL b,LL &x,LL &y) {
    if (!b) { x = 1, y = 0; return a; }
    LL d = ex_gcd(b, a % b, x, y);
    LL temp = x; x = y, y = temp - a / b * y;
    return d;
}

LL china(LL *W, LL *B, LL k) {
    LL x, y, a = 0, m, n = 1;
    for (LL i = 0; i < k; ++ i) n *= W[i];
    for (LL i = 0; i < k; ++ i) {
        m = n / W[i];
        ex_gcd(W[i], m, x, y);
        a = (a + y * m * B[i]) % n;
    }
    return (a + n) % n;
}

不定期更新ing...

 

模板整理

标签：n+1   路径压缩   最短路   前缀数组   center   style   树根   dfs   printf   

原文地址：https://www.cnblogs.com/hkttg/p/9277847.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！