标签:情况 但我 int list 之间 scan cst margin eof
一条单向的铁路线上,依次有编号为 1,2,…,n 的 n个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x ,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站( 2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。
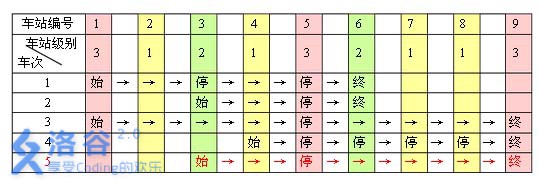
现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。
输入格式:
第一行包含 2 个正整数 n,m,用一个空格隔开。
第 i+1 行 (1≤i≤m) 中,首先是一个正整数 si(2≤si≤n) ,表示第 i 趟车次有 si 个停靠站;接下来有 si 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式:
一个正整数,即 n个火车站最少划分的级别数。
很多大佬都用了拓扑排序,这是个好思想,但我太弱了不会用
我的这个树形DP的连边和很多大佬很像,每一条线路分别处理
如果某个点在起点到终点范围内,且没有停靠,由题意可知,这几站一定比停靠站的等级低,我就从停靠的站向不停靠的站连边,表示大小关系,当然,我不连重边
然后我开始遍历一遍所有的点,如果这个点没有入边,就说明它可能是最大的,我从这个点跑树形DP,每上升一层,大小+1,我们用动规找到最大层数,就是这个根点的答案
当然,我要求的是全图层数,当然要写一个max来比较了。
#include<iostream> #include<cstdio> #include<cstring> #define rii register int i #define rij register int j using namespace std; struct cz{ int rd,cd,to[1005]; }x[1005]; int n,bj[1005],ans,tk[1005],bs,kkk,ltt,m,gh[1005][1005],as[1005],sf[1005]; void jb(int bh) { x[bh].rd+=ltt; for(rii=1;i<=ltt;i++) { if(gh[bh][tk[i]]==0) { bs++; x[tk[i]].cd++; x[tk[i]].to[x[tk[i]].cd]=bh; gh[bh][tk[i]]=1; } } } void dplast(int wz) { for(rii=1;i<=x[wz].cd;i++) { if(sf[x[wz].to[i]]==0) { dplast(x[wz].to[i]); sf[x[wz].to[i]]=1; } as[wz]=max(as[wz],as[x[wz].to[i]]+1); } } int main() { scanf("%d%d",&n,&m); for(rii=1;i<=m;i++) { int st,fi; memset(bj,0,sizeof(bj)); scanf("%d",<t); for(rij=1;j<=ltt;j++) { scanf("%d",&kkk); tk[j]=kkk; bj[kkk]=1; if(j==1) { st=kkk; } if(j==ltt) { fi=kkk; } } for(rij=st+1;j<fi;j++)//建边 { if(bj[j]==0) { jb(j); } } } for(rii=1;i<=n;i++) { if(x[i].cd==0)//初始化,如果是叶子节点,就不需要向下寻找,层数默认是1 { as[i]=1; sf[i]=1; } } int maxn=0; for(rii=1;i<=n;i++) { if(x[i].rd==0) { dplast(i); } } for(rii=1;i<=n;i++) { maxn=max(maxn,as[i]); } cout<<maxn; }
标签:情况 但我 int list 之间 scan cst margin eof
原文地址:https://www.cnblogs.com/ztz11/p/9280160.html