Matlab_xcorr_互相关函数的讨论 [未完成]

clc
clear
close

%  实现 xcorr 函数

% 基本设置
T = 1;              % [s] 总时间长度
fs = 5000;          % [Hz] 采样频率
t = 0:1/fs:T;       % [s] 时间坐标
N = length(t);      % 信号个数

% 信号生成
tm = [ t(1:N) - T , t(2:N) ];       % 相关结果的时间延迟坐标轴
td1 = 0.2*T;                        % x 信号时间延迟
td2 = 0.3*T;                        % y 信号时间延迟
noise = rand(1,2*N);                % 生成了两倍时间 T 长度的噪声 [0,1]噪声
x = noise(1+round(td1*fs):N+round(td1*fs))-0.5*ones(1,N);
y = noise(1+round(td2*fs):N+round(td2*fs))-0.5*ones(1,N);

% 求取互相关
z1 = xcorr(x,y);    % Matlab 自带函数
[~,I1] = max(abs(z1));
z2 = zeros(1,N);    % 自编函数
for n = 1:length(tm)
    z2(n) = sum( x( max(1,n-N+1):min(n,N) ).*y( max(1,N-n+1):min(2*N-n,N) ) );
end
[~,I2] = max(abs(z2));
%--------------------计算说明--------------------%
% case1：               | case2:                 %
%              .N       |              .2*N-n    %
% y:  ..........        | y:       ..........    %
%           .N-n+1      |          .1            %
%              .n       |              .N        %
% x:        ..........  | x:  ..........         %
%           .1          |          .n-N+1        %
%------------------------------------------------%
err = z1-z2;        % 两种算法的差

% 绘图
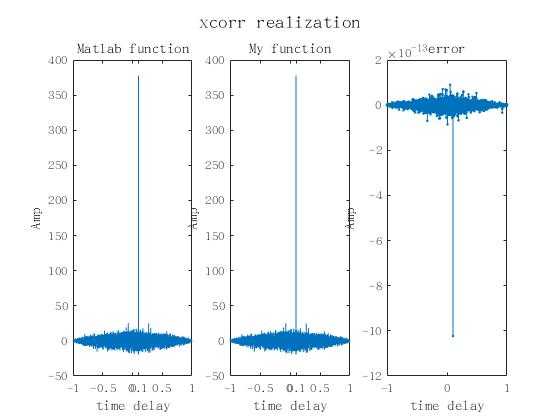
subplot(1,3,1)
    plot(tm,z1)
    title(‘Matlab function‘)
    xlabel(‘time delay‘)
    ylabel(‘Amp‘)
    a1 = gca;
    a1.XTick = sort([-1:0.5:1 tm(I1)]);
subplot(1,3,2)
    plot(tm,z2)
    title(‘My function‘)
    xlabel(‘time delay‘)
    ylabel(‘Amp‘)
    a2 = gca;
    a2.XTick = sort([-1:0.5:1 tm(I2)]);
subplot(1,3,3)
    plot(tm,err,‘.-‘)
    title(‘error‘)
    xlabel(‘time delay‘)
    ylabel(‘Amp‘)
suptitle(‘xcorr realization‘)

clc
clear
close

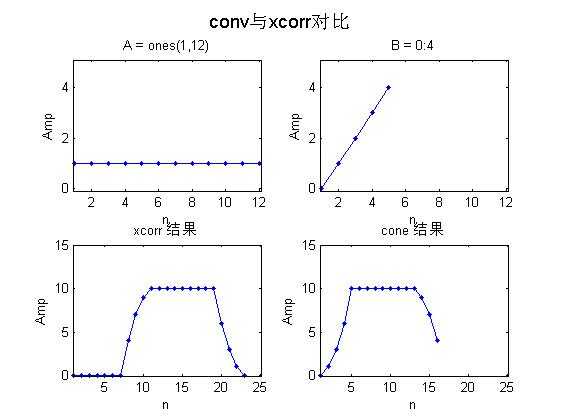
%  比较 conv xcorr

% 例子　　
A = ones(1,12);
B = 0:4;
C = xcorr(A,B);
D = conv(A,B);

%绘图
subplot(2,2,1)
    plot(A,‘.-‘)
    ylim([ -0.1 5.1 ])
    xlim([ 0.9 12.1])
    title(‘A = ones(1,12)‘)
    xlabel(‘n‘)
    ylabel(‘Amp‘)
subplot(2,2,2)
    plot(B,‘.-‘)
    ylim([ -0.1 5.1 ])
    xlim([ 0.9 12.1])
    title(‘B = 0:4‘)
    xlabel(‘n‘)
    ylabel(‘Amp‘)
subplot(2,2,3)
    plot(C,‘.-‘)
    ylim([ -0.1 15.1 ])
    xlim([ 0.9 25.1])
    title(‘xcorr 结果‘)
    xlabel(‘n‘)
    ylabel(‘Amp‘)
subplot(2,2,4)
    plot(D,‘.-‘)
    ylim([ -0.1 15.1 ])
    xlim([ 0.9 25.1])
    title(‘cone 结果‘)
    xlabel(‘n‘)
    ylabel(‘Amp‘)
suptitle(‘conv与xcorr对比‘)