数据结构（三十八）平衡二叉树（AVL树）

标签：左右子树   定义   树的定义   sel   tor   特性   于平   lan   width   

　　一、平衡二叉树的定义

　　平衡二叉树（Self-Balancing Binary Search Tree或Height-Balanced Binary Search Tree），是一种二叉排序树，其中每一个结点的左子树和右子树的高度差至多等于1。平衡二叉树是一种高度平衡的二叉排序树，即要么是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

　　将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF（Balance Factor），那么平衡二叉树上所有结点的平衡因子只可能是-1、0和1。

　　距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，称为最小不平衡树。

　　二、平衡二叉树的实现原理

　　平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入破坏了树的平衡性，若是，则找出最小不平衡树。在保持二叉排序树特性的前提下，调整最小不平衡树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

　　以数组{3,2,1,4,5,6,7,10,9,8}为例：

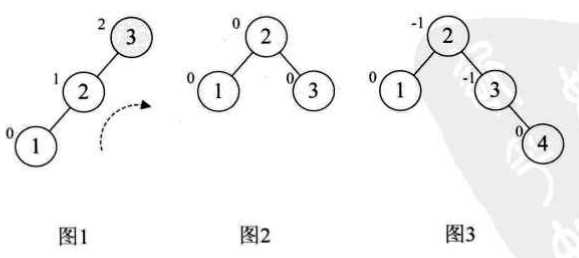
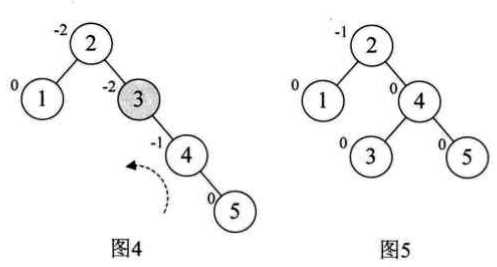
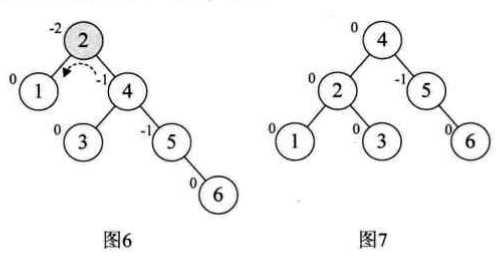
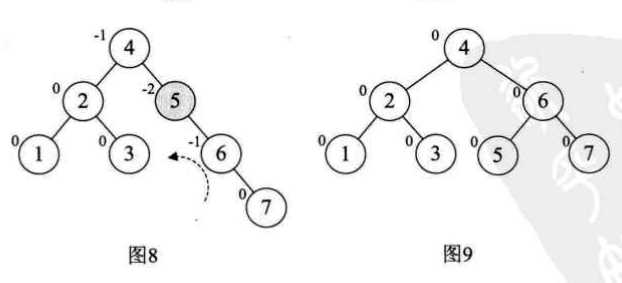
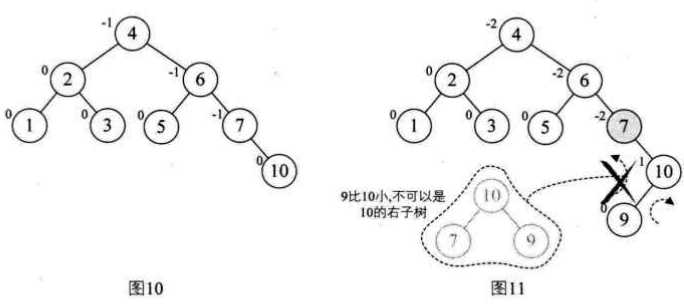
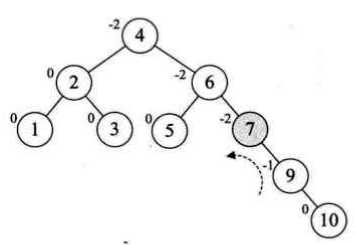
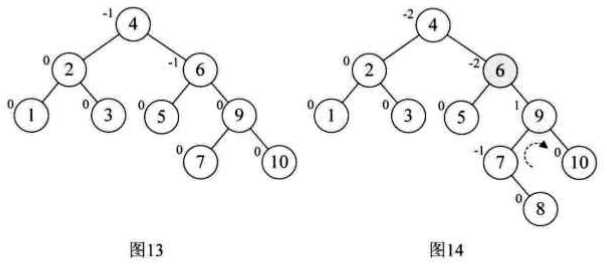
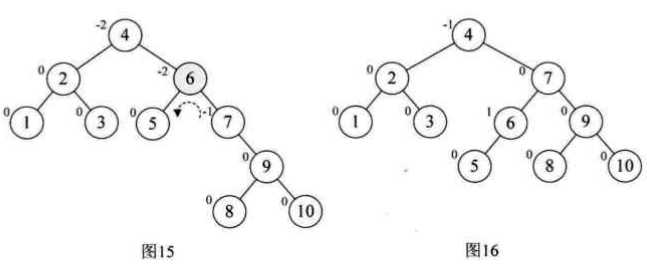
　　注意的是：

• 图6到图7，对结点2进行左旋，本来结点3是结点4的左孩子，由于旋转后需要满足二叉排序树的特定，因此结点3最后成了结点2的右孩子。
• 另外，图11中， 如果对结点7进行左旋的话，结点9就成了结点10的右孩子了，这也是不满足二叉排序树的，根本原因在于结点7的BF值为-2，二结点10的BF值为1，符号并不统一，因此不能直接旋转，所以需要首先把结点10进行右旋，结点10就成了结点9的右孩子，而此时结点7和结点9的符号也统一了，所以以结点7为根进行左旋，最后得到图13。
• 图14中同理，结点6的BF值为-2，而结点9的BF为1，所以要先以9为根结点右旋，得到图15，然后，此时结点6和结点7的BF值都为负，然后进行左旋即可。

　　三、平衡二叉排序树的实现

　　1.在平衡二叉排序树T上插入一个新纪录x的算法描述：

• 若AVL为空树，则插入一个记录为x的新结点作为T的根结点，树的深度增1
• 若x的关键字值和AVL树T的根结点的关键字值相等，则不进行插入操作
• 若x的关键字值小于AVL树的根结点的关键字值，则将x插入在概述的左子树上，并且当插入之后的左子树深度增加1时，分别就下列不同情况进行处理：

　　①若AVL树的根结点的平衡因子为-1（右子树的深度大于左子树的深度），则将根结点的平衡因子调整为0，并且树的深度不变。

　　②若AVL树的根结点的平衡因子为0（左右子树的深度相等），则将根结点的平衡因子调整为1，树的深度同时增加1

　　③若AVL树的根结点的平衡因子为1（左子树的深度大于右子树的深度），则当该树的左子树的根结点的平衡因子为1时需要进行单向右旋；当该树的左子树的根结点的平衡因子为-1时需进行先左旋后右旋。

• 若x的关键字值大于AVL树的根结点的关键字值，则将x插入在该树的右子树上，并且当插入之后的右子树深度增加1时，分别就不同情况进行处理，同理第三步。

　　四、平衡二叉排序树的时间复杂度

　　平衡二叉排序树使得二叉树排序树的结构更好，从而提高了查找操作的速度。但是使得插入和删除操作复杂化，从而降低了插入和删除操作的速度。因此，平衡二叉树适合于二叉排序树一经建立就很少进行插入和删除操作，而主要是进行查找操作的应用场合中。

　　由于平衡二叉树在查找过程中和给定值进行比较的关键字个数不超过树的深度，因此，在平衡二叉树上进行查找的时间复杂度为O(logn)。

数据结构（三十八）平衡二叉树（AVL树）

标签：左右子树   定义   树的定义   sel   tor   特性   于平   lan   width   

原文地址：https://www.cnblogs.com/BigJunOba/p/9286401.html