标签:遍历 函数 元素 需要 中序遍历 最大的 解决 树的定义 插入
一、多路查找树的背景
前面所讨论的查找算法都是在内存中进行的,它们适用于较小的文件,而对于较大的、存放在外存储器上的文件就不合适了,对于此类大规模的文件,即使是采用了平衡二叉树,在查找效率上仍然较低。
如果要操作的数据集非常大,大到内存已经没办法处理了,这种情况下,对数据的处理需要不断从硬盘等存储设备中调入或调出内存页面。一旦涉及到这样的外部设备,关于时间复杂度的计算就会发生变化,访问该集合元素的时间已经不仅仅是寻找该元素所需比较次数的函数,必须考虑对硬盘等外部存储设备的访问时间以及将会对该设备做出多少次的单独访问。
二、多路查找树的定义
之前的树都是一个结点可以有多个孩子,但是它自身只存储一个元素,二叉树限制更多,结点最多只能有两个孩子。一个结点只能存储一个元素,在元素非常多的时候,就使得要么树的度非常大(结点拥有子树的个数的最大值),要么树的高度非常大,甚至两者都必须足够大才行。这就使得内存存取外存次数非常多,这显然成了时间效率上的瓶颈,因此,需要打破每一个结点只存储一个元素的限制。
多路查找树(muiti-way search tree),其每一个结点的孩子树可以多于两个,且每一个结点处可以存储多个元素。
三、2-3树
2-3树的定义:
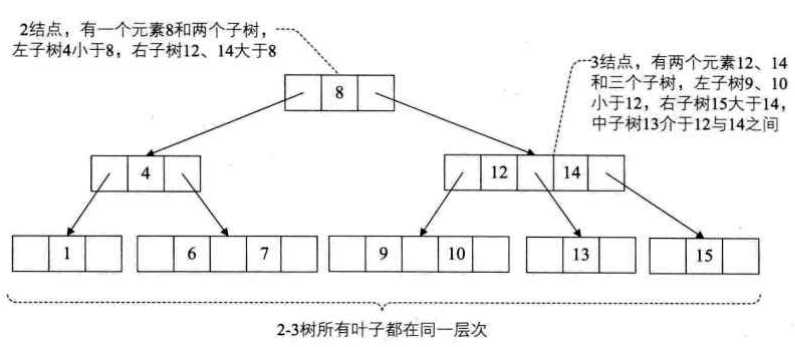
四、2-3-4树
2-3-4树就是2-3树的拓展,包括了4结点的使用。一个4结点包含小中大三个数据元素和四个孩子(或没有孩子),一个4结点要么没有孩子,要么有4个孩子。如果某个4结点有孩子的话,左子树包含小于最小元素的元素;第二子树包含大于最小元素,小于第二元素的元素;第三子树包含大于第二元素,小于最大元素的元素;右子树包含大于最大元素的元素。
2-3-4树的插入过程(插入顺序为{7,1,2,5,6,9,8,4,3}):
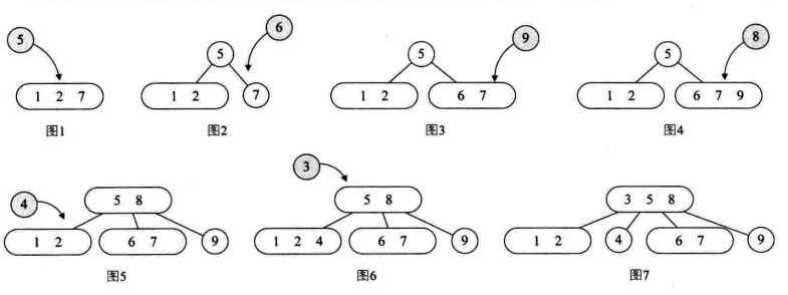
2-3-4树的删除过程(删除顺序为:{1,6,3,4,5,2,9}):
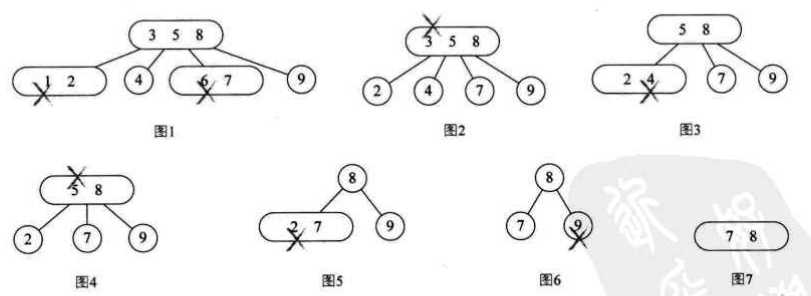
五、B树
B树(B-Tree)是一种平衡的多路查找树,2-3树和2-3-4树都是B树的特例。结点最大的孩子数目称为B树的阶(order),因此,2-3树是3阶B树,2-3-4树是4阶B树。
一个m阶的B树具有如下属性:

六、B+树
B树还是有缺陷的,对于树结构来说,可以通过中序遍历来顺序查找树中的元素,这一切都是在内存中进行。但是在B树中,往返于每个结点就意味着,必须得在硬盘的页面之间进行多次访问,例如,遍历下面这棵B树,假设每个结点都属于硬盘的不同页面,中序遍历所有元素就需要访问:页面2→页面1→页面3→页面1→页面4→页面1→页面5。即每次经过结点遍历时,都会对结点中的元素进行一次遍历,如何让遍历时每个元素只访问一次就成了需要解决的问题。
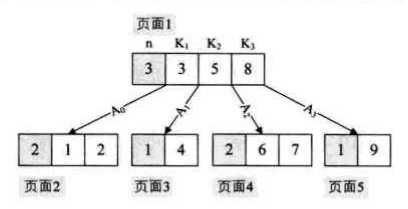
B+树是在原有的B树结构基础上,加上了新的元素组织方式。B+树是应文件系统所需而出的一种B树的变形树,在B树中,每一个元素在该树中只出现一次,有可能在叶子结点上,也有可能在分支结点上。而在B+树中,出现在分支结点中的元素会被当做它们在该分支结点位置的中序后继者(叶子结点)中再次列出。另外,每一个叶子节点都会保存一个指向后一叶子结点的指针。
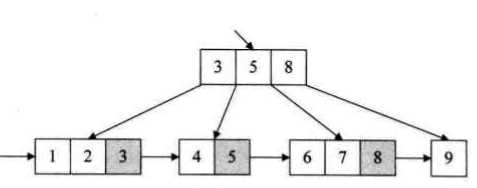
一棵m阶的B+树和m阶的B树的差异在于:
标签:遍历 函数 元素 需要 中序遍历 最大的 解决 树的定义 插入
原文地址:https://www.cnblogs.com/BigJunOba/p/9288150.html