标签:table package 代码 was 相关信息 介绍 i++ 初始 final
前面我们介绍了树这种数据结构,树是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合,把它叫做“树”是因为它看起来像一棵倒挂的树,包括二叉树、红黑树、2-3-4树、堆等各种不同的树,有对这几种树不了解的可以参考我前面几篇博客。而本篇博客我们将介绍另外一种数据结构——图,图也是计算机程序设计中最常用的数据结构之一,从数学意义上讲,树是图的一种,大家可以对比着学习。
我们知道,前面讨论的数据结构都有一个框架,而这个框架是由相应的算法实现的,比如二叉树搜索树,左子树上所有结点的值均小于它的根结点的值,右子树所有结点的值均大于它的根节点的值,类似这种形状使得它容易搜索数据和插入数据,树的边表示了从一个节点到另一个节点的快捷方式。
而图通常有个固定的形状,这是由物理或抽象的问题所决定的。比如图中节点表示城市,而边可能表示城市间的班机航线。如下图是美国加利福利亚简化的高速公路网:
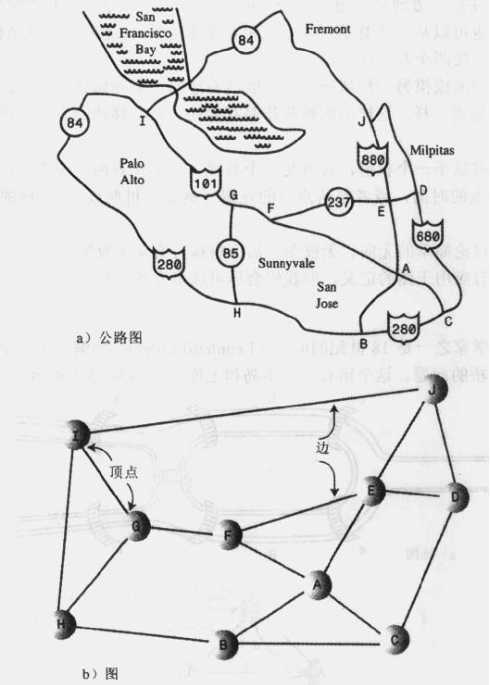
如果两个顶点被同一条边连接,就称这两个顶点是邻接的,如上图 I 和 G 就是邻接的,而 I 和 F 就不是。有时候也将和某个指定顶点邻接的顶点叫做它的邻居,比如顶点 G 的邻居是 I、H、F。
路径是边的序列,比如从顶点B到顶点J的路径为 BAEJ,当然还有别的路径 BCDJ,BACDJ等等。
如果至少有一条路径可以连接起所有的顶点,那么这个图称作连通的;如果假如存在从某个顶点不能到达另外一个顶点,则称为非联通的。
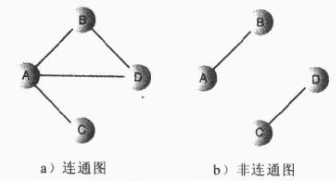
如果图中的边没有方向,可以从任意一边到达另一边,则称为无向图;比如双向高速公路,A城市到B城市可以开车从A驶向B,也可以开车从B城市驶向A城市。但是如果只能从A城市驶向B城市的图,那么则称为有向图。
图中的边被赋予一个权值,权值是一个数字,它能代表两个顶点间的物理距离,或者从一个顶点到另一个顶点的时间,这种图被称为有权图;反之边没有赋值的则称为无权图。
本篇博客我们讨论的是无权无向图。
我们知道图是由顶点和边组成,那么在计算机中,怎么来模拟顶点和边?
在大多数情况下,顶点表示某个真实世界的对象,这个对象必须用数据项来描述。比如在一个飞机航线模拟程序中,顶点表示城市,那么它需要存储城市的名字、海拔高度、地理位置和其它相关信息,因此通常用一个顶点类的对象来表示一个顶点,这里我们仅仅在顶点中存储了一个字母来标识顶点,同时还有一个标志位,用来判断该顶点有没有被访问过(用于后面的搜索)。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
/** * 顶点类 * @author vae */public class Vertex { public char label; public boolean wasVisited; public Vertex(char label){ this.label = label; wasVisited = false; }} |
顶点对象能放在数组中,然后用下标指示,也可以放在链表或其它数据结构中,不论使用什么结构,存储只是为了使用方便,这与边如何连接点是没有关系的。
在前面讲解各种树的数据结构时,大多数树都是每个节点包含它的子节点的引用,比如红黑树、二叉树。也有用数组表示树,树组中节点的位置决定了它和其它节点的关系,比如堆就是用数组表示。
然而图并不像树,图没有固定的结构,图的每个顶点可以与任意多个顶点相连,为了模拟这种自由形式的组织结构,用如下两种方式表示图:邻接矩阵和邻接表(如果一条边连接两个顶点,那么这两个顶点就是邻接的)
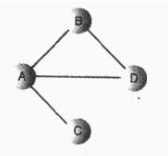
邻接矩阵:
邻接矩阵是一个二维数组,数据项表示两点间是否存在边,如果图中有 N 个顶点,邻接矩阵就是 N*N 的数组。上图用邻接矩阵表示如下:

1表示有边,0表示没有边,也可以用布尔变量true和false来表示。顶点与自身相连用 0 表示,所以这个矩阵从左上角到右上角的对角线全是 0 。
注意:这个矩阵的上三角是下三角的镜像,两个三角包含了相同的信息,这个冗余信息看似低效,但是在大多数计算机中,创造一个三角形数组比较困难,所以只好接受这个冗余,这也要求在程序处理中,当我们增加一条边时,比如更新邻接矩阵的两部分,而不是一部分。
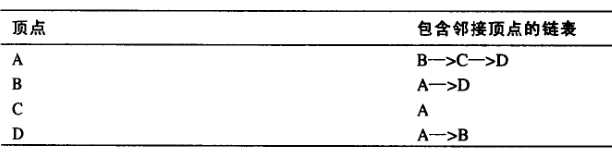
邻接表:
邻接表是一个链表数组(或者是链表的链表),每个单独的链表表示了有哪些顶点与当前顶点邻接。
在图中实现最基本的操作之一就是搜索从一个指定顶点可以到达哪些顶点,比如从武汉出发的高铁可以到达哪些城市,一些城市可以直达,一些城市不能直达。现在有一份全国高铁模拟图,要从某个城市(顶点)开始,沿着铁轨(边)移动到其他城市(顶点),有两种方法可以用来搜索图:深度优先搜索(DFS)和广度优先搜索(BFS)。它们最终都会到达所有连通的顶点,深度优先搜索通过栈来实现,而广度优先搜索通过队列来实现,不同的实现机制导致不同的搜索方式。
深度优先搜索算法有如下规则:
规则1:如果可能,访问一个邻接的未访问顶点,标记它,并将它放入栈中。
规则2:当不能执行规则 1 时,如果栈不为空,就从栈中弹出一个顶点。
规则3:如果不能执行规则 1 和规则 2 时,就完成了整个搜索过程。
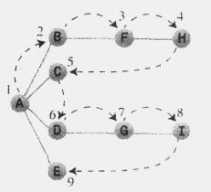
对于上图,应用深度优先搜索如下:假设选取 A 顶点为起始点,并且按照字母优先顺序进行访问,那么应用规则 1 ,接下来访问顶点 B,然后标记它,并将它放入栈中;再次应用规则 1,接下来访问顶点 F,再次应用规则 1,访问顶点 H。我们这时候发现,没有 H 顶点的邻接点了,这时候应用规则 2,从栈中弹出 H,这时候回到了顶点 F,但是我们发现 F 也除了 H 也没有与之邻接且未访问的顶点了,那么再弹出 F,这时候回到顶点 B,同理规则 1 应用不了,应用规则 2,弹出 B,这时候栈中只有顶点 A了,然后 A 还有未访问的邻接点,所有接下来访问顶点 C,但是 C又是这条线的终点,所以从栈中弹出它,再次回到 A,接着访问 D,G,I,最后也回到了 A,然后访问 E,但是最后又回到了顶点 A,这时候我们发现 A没有未访问的邻接点了,所以也把它弹出栈。现在栈中已无顶点,于是应用规则 3,完成了整个搜索过程。
深度优先搜索在于能够找到与某一顶点邻接且没有访问过的顶点。这里以邻接矩阵为例,找到顶点所在的行,从第一列开始向后寻找值为1的列;列号是邻接顶点的号码,检查这个顶点是否未访问过,如果是这样,那么这就是要访问的下一个顶点,如果该行没有顶点既等于1(邻接)且又是未访问的,那么与指定点相邻接的顶点就全部访问过了(后面会用算法实现)。
深度优先搜索要尽可能的远离起始点,而广度优先搜索则要尽可能的靠近起始点,它首先访问起始顶点的所有邻接点,然后再访问较远的区域,这种搜索不能用栈实现,而是用队列实现。
规则1:访问下一个未访问的邻接点(如果存在),这个顶点必须是当前顶点的邻接点,标记它,并把它插入到队列中。
规则2:如果已经没有未访问的邻接点而不能执行规则 1 时,那么从队列列头取出一个顶点(如果存在),并使其成为当前顶点。
规则3:如果因为队列为空而不能执行规则 2,则搜索结束。
对于上面的图,应用广度优先搜索:以A为起始点,首先访问所有与 A 相邻的顶点,并在访问的同时将其插入队列中,现在已经访问了 A,B,C,D和E。这时队列(从头到尾)包含 BCDE,已经没有未访问的且与顶点 A 邻接的顶点了,所以从队列中取出B,寻找与B邻接的顶点,这时找到F,所以把F插入到队列中。已经没有未访问且与B邻接的顶点了,所以从队列列头取出C,它没有未访问的邻接点。因此取出 D 并访问 G,D也没有未访问的邻接点了,所以取出E,现在队列中有 FG,在取出 F,访问 H,然后取出 G,访问 I,现在队列中有 HI,当取出他们时,发现没有其它为访问的顶点了,这时队列为空,搜索结束。
实现深度优先搜索的栈 StackX.class
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
package com.ys.graph;public class StackX { private final int SIZE = 20; private int[] st; private int top; public StackX(){ st = new int[SIZE]; top = -1; } public void push(int j){ st[++top] = j; } public int pop(){ return st[top--]; } public int peek(){ return st[top]; } public boolean isEmpty(){ return (top == -1); }} |
实现广度优先搜索的队列Queue.class
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
package com.ys.graph;public class Queue { private final int SIZE = 20; private int[] queArray; private int front; private int rear; public Queue(){ queArray = new int[SIZE]; front = 0; rear = -1; } public void insert(int j) { if(rear == SIZE-1) { rear = -1; } queArray[++rear] = j; } public int remove() { int temp = queArray[front++]; if(front == SIZE) { front = 0; } return temp; } public boolean isEmpty() { return (rear+1 == front || front+SIZE-1 == rear); }} |
图代码 Graph.class
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
|
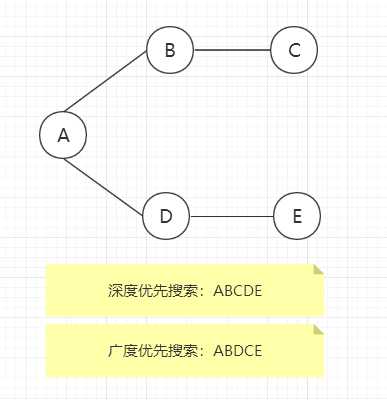
package com.ys.graph;public class Graph { private final int MAX_VERTS = 20;//表示顶点的个数 private Vertex vertexList[];//用来存储顶点的数组 private int adjMat[][];//用邻接矩阵来存储 边,数组元素0表示没有边界,1表示有边界 private int nVerts;//顶点个数 private StackX theStack;//用栈实现深度优先搜索 private Queue queue;//用队列实现广度优先搜索 /** * 顶点类 * @author vae */ class Vertex { public char label; public boolean wasVisited; public Vertex(char label){ this.label = label; wasVisited = false; } } public Graph(){ vertexList = new Vertex[MAX_VERTS]; adjMat = new int[MAX_VERTS][MAX_VERTS]; nVerts = 0;//初始化顶点个数为0 //初始化邻接矩阵所有元素都为0,即所有顶点都没有边 for(int i = 0; i < MAX_VERTS; i++) { for(int j = 0; j < MAX_VERTS; j++) { adjMat[i][j] = 0; } } theStack = new StackX(); queue = new Queue(); } //将顶点添加到数组中,是否访问标志置为wasVisited=false(未访问) public void addVertex(char lab) { vertexList[nVerts++] = new Vertex(lab); } //注意用邻接矩阵表示边,是对称的,两部分都要赋值 public void addEdge(int start, int end) { adjMat[start][end] = 1; adjMat[end][start] = 1; } //打印某个顶点表示的值 public void displayVertex(int v) { System.out.print(vertexList[v].label); } /**深度优先搜索算法: * 1、用peek()方法检查栈顶的顶点 * 2、用getAdjUnvisitedVertex()方法找到当前栈顶点邻接且未被访问的顶点 * 3、第二步方法返回值不等于-1则找到下一个未访问的邻接顶点,访问这个顶点,并入栈 * 如果第二步方法返回值等于 -1,则没有找到,出栈 */ public void depthFirstSearch() { //从第一个顶点开始访问 vertexList[0].wasVisited = true; //访问之后标记为true displayVertex(0);//打印访问的第一个顶点 theStack.push(0);//将第一个顶点放入栈中 while(!theStack.isEmpty()) { //找到栈当前顶点邻接且未被访问的顶点 int v = getAdjUnvisitedVertex(theStack.peek()); if(v == -1) { //如果当前顶点值为-1,则表示没有邻接且未被访问顶点,那么出栈顶点 theStack.pop(); }else { //否则访问下一个邻接顶点 vertexList[v].wasVisited = true; displayVertex(v); theStack.push(v); } } //栈访问完毕,重置所有标记位wasVisited=false for(int i = 0; i < nVerts; i++) { vertexList[i].wasVisited = false; } } //找到与某一顶点邻接且未被访问的顶点 public int getAdjUnvisitedVertex(int v) { for(int i = 0; i < nVerts; i++) { //v顶点与i顶点相邻(邻接矩阵值为1)且未被访问 wasVisited==false if(adjMat[v][i] == 1 && vertexList[i].wasVisited == false) { return i; } } return -1; } /** * 广度优先搜索算法: * 1、用remove()方法检查栈顶的顶点 * 2、试图找到这个顶点还未访问的邻节点 * 3、 如果没有找到,该顶点出列 * 4、 如果找到这样的顶点,访问这个顶点,并把它放入队列中 */ public void breadthFirstSearch(){ vertexList[0].wasVisited = true; displayVertex(0); queue.insert(0); int v2; while(!queue.isEmpty()) { int v1 = queue.remove(); while((v2 = getAdjUnvisitedVertex(v1)) != -1) { vertexList[v2].wasVisited = true; displayVertex(v2); queue.insert(v2); } } //搜索完毕,初始化,以便于下次搜索 for(int i = 0; i < nVerts; i++) { vertexList[i].wasVisited = false; } } public static void main(String[] args) { Graph graph = new Graph(); graph.addVertex(‘A‘); graph.addVertex(‘B‘); graph.addVertex(‘C‘); graph.addVertex(‘D‘); graph.addVertex(‘E‘); graph.addEdge(0, 1);//AB graph.addEdge(1, 2);//BC graph.addEdge(0, 3);//AD graph.addEdge(3, 4);//DE System.out.println("深度优先搜索算法 :"); graph.depthFirstSearch();//ABCDE System.out.println(); System.out.println("----------------------"); System.out.println("广度优先搜索算法 :"); graph.breadthFirstSearch();//ABDCE }} |
测试结果:
对于图的操作,还有一个最常用的就是找到最小生成树,最小生成树就是用最少的边连接所有顶点。对于给定的一组顶点,可能有很多种最小生成树,但是最小生成树的边的数量 E 总是比顶点 V 的数量小1,即:
V = E + 1
这里不用关心边的长度,不是找最短的路径(会在带权图中讲解),而是找最少数量的边,可以基于深度优先搜索和广度优先搜索来实现。
比如基于深度优先搜索,我们记录走过的边,就可以创建一个最小生成树。因为DFS 访问所有顶点,但只访问一次,它绝对不会两次访问同一个顶点,但她看到某条边将到达一个已访问的顶点,它就不会走这条边,它从来不遍历那些不可能的边,因此,DFS 算法走过整个图的路径必定是最小生成树。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
//基于深度优先搜索找到最小生成树public void mst(){ vertexList[0].wasVisited = true; theStack.push(0); while(!theStack.isEmpty()){ int currentVertex = theStack.peek(); int v = getAdjUnvisitedVertex(currentVertex); if(v == -1){ theStack.pop(); }else{ vertexList[v].wasVisited = true; theStack.push(v); displayVertex(currentVertex); displayVertex(v); System.out.print(" "); } } //搜索完毕,初始化,以便于下次搜索 for(int i = 0; i < nVerts; i++) { vertexList[i].wasVisited = false; }} |
标签:table package 代码 was 相关信息 介绍 i++ 初始 final
原文地址:https://www.cnblogs.com/zhoanghua/p/9289100.html