标签:style blog http io ar strong 数据 sp 2014
1)主要原因:一直以来,我觉得计划对于实现目标非常重要。但是从2010年至今,我的各种各样计划几乎都全部流产,以至于我丧失了对于制定计划的兴趣。当然,抛弃制定计划之后,我仍然没有能够完成我的目标。翻看往年计划本,2013年2月份的时候,我的计划中就提到了问题的根源可能在于在于制定计划的方法上,但是没有加以重视。
2)催化剂:今年两次考GRE以及一次托福考试,匆匆忙忙的抢考位、预定酒店、车票和机票,然后临时抱佛脚,最后结果也十分不理想。仔细分析,解决问题的方法并没有什么缺陷,主要缺陷在于执行力度不够。基于这些事实,我不得不承认我一直以来对大多事务都存在有傲慢和自以为是的情绪,以至于我压根都没有意识到关键的问题在于计划,而且也没有意识到,我根本就没有在执行计划。
3)偶然因素:幸运的是,我找到了一种抛弃主观傲慢及焦虑情绪来解决问题的方法(这一点非常重要)。因此,在此基础上,我首先开始了广泛的信息搜集。这个信息检索的过程并没有持续很久,因为现有的大部分的制定计划的方法都是基于我之前的思考模型。直到我看到了一位在Google London工作的Lucida提出了TARQIE法,即一种“量化”自己进步的方法。当然,这里的量化,并不是真正的量化。但是,博主Lucida借鉴了机器学习的模型,从而来完善自己的学习模型,启发了我的思考。
从Lucida的博文中,我们可以引用其归纳的模型:
这个模型提出后,可以用一个小的例子进行分析。
假如甲同学有1个月的时间,备考CET6。
阅读如何达到要求?工作量/时间?
填空如何达到要求?工作量/时间?
作文如何达到要求?工作量/时间?
3.步骤三:根据上述要求,计算并安排时间。
Lucida提出的这个计划制定模型,非常简单又清晰的强调了制定计划中非常重要的概念:改进和验证。“改进”能够保证计划的弹性,而“验证”则保障了计划的成效。
附:Lucida的原文链接http://zh.lucida.me/blog/tarqie-a-quantized-continous-growing-approach/)
为了更加客观的研究如何实现某一个目标,我认为需要将实现目标这个过程以及其中的影响因素进一步抽象出来,这样才能更加清晰的反映其中的规律。
在晚上吃饭的时候,我慢慢的走在路上,考虑如何解决这样的一个问题,有意思的是,我居然真的找到了一个类似的过程。这个思想在机械制造、数控机床、等课程当中非常常见,或者控制理论中非常常用。具体而言,这个过程可以演化为如何精确地用机器控制物体X 从A位置移动到B位置。机器是怎样执行这个过程的呢?
1)确定A和B各自的位置坐标,计算位置差。确定机器移动总距离
2)将总距离分成若干步。根据具体的精度要求,可以对每一步进行插值(就是细化)。
3)每走一步,反馈X实际的位置(由于机器等各方面因素会造成误差),计算X与目标B位置的实际距离,重新计算步长。
4)重复上述过程,逐步逼近B位置附近(误差范围内)。
窃以为在完成目标的过程中,也可以用类似的IFA(Interpolation, Feedback, Approximation)法进行。
基于此,我们不妨首先定义(这个定义是从实现目标的角度进行,至于解决如何确定目标这个过程,则应该采用其他的模型,定义也会不同,此处不在探讨范围之内,故先提出以免误用)目标为:
在规定的时间t内,在扰动I的作用下从情形A到达情形B,以逼近需求D。
为了简便,标记为G|t:AàB~D。
其中:情形A或者B定义为所有能够影响A—B过程的状态量在起始时刻或者终点时刻。
从这个表达式中,我们可以认为确定目标的几个关键要素为:
1.需求D
这里讨论的情形都是在需求清晰的情况下,故认为已知。
2.时间t
需求的清晰,意味着截止时间的确定。且默认t时间一定是大于理论时间。
3.情形(状态)
“情形”这个集合中包含了两层状态:(我认为是包含的关系而非并列)
如上图:GENERAL部分,是P的固有属性。
例如:备考CET6中,P的待人接物的方式、P的世界观等,都应该属于GENERAL。而SPECIFIC则应该具体包括针对这个目标的所有技能,直接反映了需求D的属性,比如P的阅读速度、词汇量等。
这两者之间的关系应该具有以下几个特征:
1)在时间t较短的情况下以及A与B差距不大的情况下,general可以忽略。
2)在时间t较长的情况下,或者A与B差距较大的情况下,general 往往是制约因素,但是难以改善。
4.扰动M
不妨暂且把扰动定义为:能够影响目标完成的因素。
扰动可以分为:有益扰动、无益扰动。根据扰动发生的时间特点,又分为连续、随机、狄拉克等等。
首先讨论最简单的情况,利用插值(Interpolation)反馈(feedback)逼近(approximation)的方法--IFA在没有扰动情况下的求解(理想状态)求解:
1)根据D,分析所有影响A/B情形的因素。根据t的长短,估测各因素权重及增益系数。
2)为了保证最后能满足D,所以B应该属于满足D的最高要求,或者B大于D的置信区间的下沿。确定A与B差值。
3)对时间t进行粗分段。t=t1+t2+t3+…+tn
4)对t1时间段进行细分,到达中间情形M1。
5)确定M1与B的距离。对t2过程进行调整后细分,到达中间情形M2。
6)重复5)直到tn结束。
7)验证结果。总结失败或者成功原因,记录判断参数,作为下一次求解参考。
再来讨论有扰动的情况求解,此处仅仅讨论无益扰动。
1)一次性无益扰动。
求解方法为:在粗分段以及细分段过程中,预留出一次性扰动的时间,这样更加逼近真实值,增加了最后的到达精度。
2)连续无益扰动或离散周期扰动。
求解方法为:延长时间t。一般为提早起始时间,也可以推后终止时间。因此,在确定时间长度t时,最好预留kt时间,k值为经验系数。在没有办法提早起始时间的情况下,只能提高每段时间内的工作量。
3)Irreparable扰动
求解方法:改变G值。
最后讨论一下实际执行时往往会出现的多目标并行:
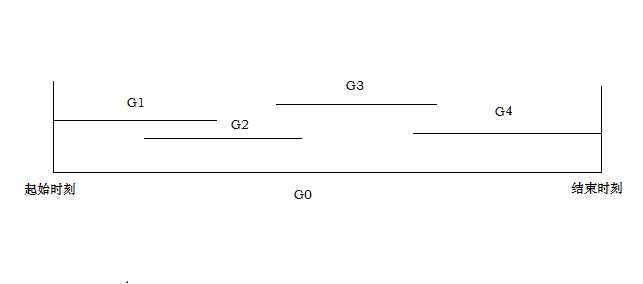
如上图所示代表一个典型的多目标并行过程,G0表示某段总的时间t内,需要分别按照一定次序完成G1、G2、G3、G4等若干个目标。
简单的情况为,每一个目标分别独立,并且在总时间段t内不会再重复。
换言之,某一个目标失败,不会对其他目标的造成影响。
在这样的一个过程中,关键的节点包括:
)每个G开始的时刻和结束的时刻。
2)衔接部分。即从两个G交叉的部分。
解决的办法包括:
1)避免多目标并行,转多目标并行为单目标。即某段时间内做一件事情。这种情况通常发生在,没有临时突发目标的情况下。
2)在发生了临时重要突发目标的情况下。由于时间有限,劳动强度有限,因此尽量与原有目标进行联系、转化甚至替代,必要时进行取舍。
3)在发生了临时突发目标,但是并不是服务于G0时,以完成G0为主,临时突发目标,尽力即可,不求完成。长线目标高于临时目标。
以上所有性质,都是根据个人观察中所得。还有大量的性质没有进行描述。同时,进一步的量化有待实例中产生的数据来进行补充。
有待实践后补充。
后注:
我对于这篇文章,非常关注以下几个问题,希望读者们能够提出宝贵的建议:
1.我的表述是否清晰,是否有冗余、重复或者不清晰的地方?
2.上述说明过程中,有哪些地方你觉得根据你的经验可以进行修正?
3.你能不能给分享一些你的关于制定计划的见解和经验?
4.读了这篇文章后,你觉得这个方法是否有用,你会去执行吗?为什么?
标签:style blog http io ar strong 数据 sp 2014
原文地址:http://www.cnblogs.com/totoroclub/p/4002801.html