标签：国家   char   int   const   其他   img   dep   ons   lin   

P1791 [国家集训队]人员雇佣

首先假设所有工作人员都是己方的，现在收益是$\sum_{i!=j}2E[i][j]$，然后现在可以选一些人，炒掉其他的

对编号为$i$的人来说，选择不炒他会获得$-A[i]$的收益，所以每个点向T连一条边，权值为$A[i]$

然后，对每个点对$(i,j) (i<j)$，从S向i,j都连一条权值为E[i][j]的边，ij互相连权值为2E[i][j]的边

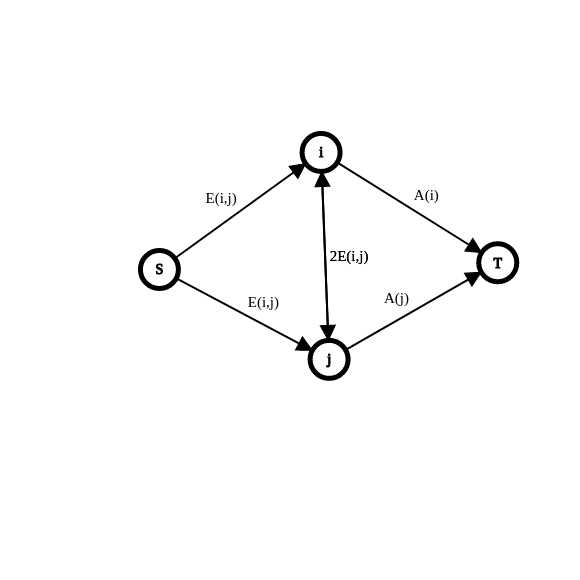
那么这样为啥是对的呢

• 如果两个都选，只需要总体割掉$A(i)(i\rightarrow T),A(j)(j\rightarrow T)$即可
• 如果只选一个，收益为0，要减掉一开始的$E(i,j)$。不妨假设选了i，那么要割$A(i)(i \rightarrow T),E(i,j)(S\rightarrow j)$
• 如果两个都选，要减掉两个$E(i,j)$，已经割掉两个$S\rightarrow i, S\rightarrow j$了

所以这非常对

然后每个点对都能这样，就可以缩边了，S向每个点连$\sum_{j=1}^nE[i][j]$的边，每个点向T连$A[i]$的边，任意两点连$2E[i][j]$的边，就没有错

注意边数巨大，为了卡常可以i到j的边不连反边，显然还是对的

#include<bits/stdc++.h>
#define il inline
#define vd void
#define rg register
#define ll long long
#define inf 1e9
il int gi(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*f;
}
const int maxn=3011,S=3009,T=3008,maxm=2e7+1;
int fir[maxn],head[maxn],dis[maxm],nxt[maxm],id=1,dep[maxn];
ll w[maxm];
il vd link(int a,int b,ll c){
    nxt[++id]=fir[a],fir[a]=id,dis[id]=b,w[id]=c;
    nxt[++id]=fir[b],fir[b]=id,dis[id]=a,w[id]=0;
}
il bool BFS(){
    static int que[maxn],hd,tl;
    hd=tl=0;
    que[tl++]=S;
    for(rg int i=1;i<=T;++i)dep[i]=0;dep[S]=1;
    while(hd^tl){
        rg int x=que[hd];
        for(int i=fir[x];i;i=nxt[i]){
            if(!dep[dis[i]]&&w[i]){
                dep[dis[i]]=dep[x]+1;
                que[tl++]=dis[i];
            }
        }
        ++hd;
    }
    return dep[T];
}
il ll Dinic(int x,ll maxflow){
    if(x==T)return maxflow;
    ll ret=0;
    for(int&i=head[x];i;i=nxt[i])
        if(w[i]&&dep[dis[i]]==dep[x]+1){
            int d=Dinic(dis[i],std::min(maxflow-ret,w[i]));
            w[i]-=d,w[i^1]+=d,ret+=d;
            if(ret==maxflow)break;
        }
    return ret;
}
ll a[maxn],e[maxn][maxn],b[maxn];
main(){
    int n=gi();ll ans=0;
    for(rg int i=1;i<=n;++i)a[i]=gi();
    for(rg int i=1;i<=n;++i)for(rg int j=1;j<=n;++j)e[i][j]=gi(),ans+=e[i][j],b[i]+=e[i][j];
    for(rg int i=1;i<=n;++i)link(S,i,b[i]),link(i,S,0),link(i,T,a[i]),link(T,i,0);
    for(rg int i=1;i<=n;++i)for(rg int j=i+1;j<=n;++j)link(i,j,2*e[i][j]),link(j,i,2*e[i][j]);
    while(BFS())memcpy(head,fir,sizeof fir),ans-=Dinic(S,inf);
    printf("%lld\n",ans);
    return 0;
}

P1791 [国家集训队]人员雇佣

标签：国家   char   int   const   其他   img   dep   ons   lin   

原文地址：https://www.cnblogs.com/ssfdJR/p/9291672.html