标签：instead   维度   接下来   目录   request   argmax   tail   ges   pytho   

深度学习是一个框架，包含多个重要算法: 

• Convolutional Neural Networks(CNN)卷积神经网络
• AutoEncoder自动编码器
• Sparse Coding稀疏编码
• Restricted Boltzmann Machine(RBM)限制波尔兹曼机
• Deep Belief Networks(DBN)深信度网络
• Recurrent neural Network(RNN)多层反馈循环神经网络神经网络

对于不同问题(图像，语音，文本)，需要选用不同网络模型比如CNN RESNET等才能达到更好效果。

今天来讲最基础的CNN网络。

可以不可以模仿人类大脑的这个特点，构造多层的神经网络，较低层的识别初级的图像特征，若干底层特征组成更上一层特征，最终通过多个层级的组合，最终在顶层做出分类呢？答案是肯定的，这也是许多深度学习算法（包括CNN）的灵感来源。

CNN网络介绍

卷积神经网络是一种多层神经网络，擅长处理图像特别是大图像的相关机器学习问题。

卷积网络通过一系列方法，成功将数据量庞大的图像识别问题不断降维，最终使其能够被训练。CNN最早由Yann LeCun提出并应用在手写字体识别上（MINST）。LeCun提出的网络称为LeNet，其网络结构如下：

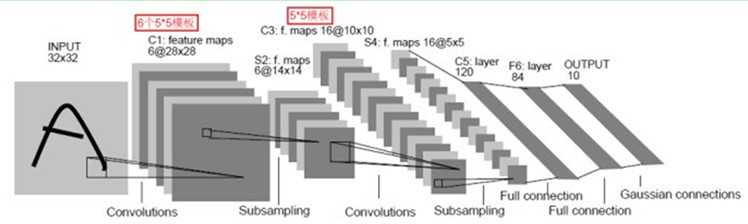
这是一个最典型的卷积网络，由卷积层、池化层、全连接层组成。其中卷积层与池化层配合，组成多个卷积组，逐层提取特征，最终通过若干个全连接层完成分类。

卷积层完成的操作，可以认为是受局部感受野概念的启发，而池化层，主要是为了降低数据维度。

综合起来说，CNN通过卷积来模拟特征区分，并且通过卷积的权值共享及池化，来降低网络参数的数量级，最后通过传统神经网络完成分类等任务。

降低参数量级

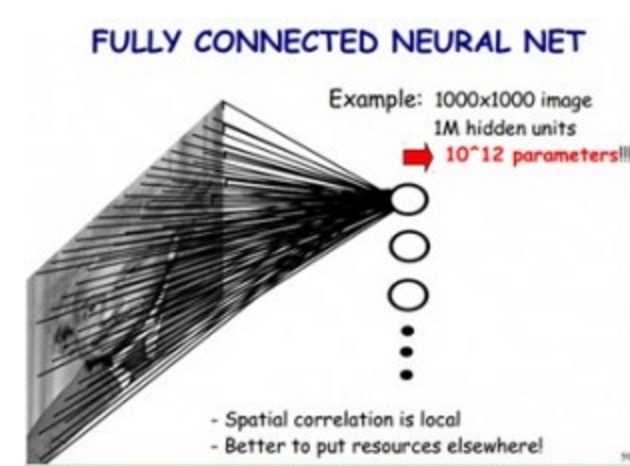
为什么要降低参数量级？从下面的例子就可以很容易理解了。

如果我们使用传统神经网络方式，对一张图片进行分类，那么，我们把图片的每个像素都连接到隐藏层节点上，那么对于一张1000x1000像素的图片，如果我们有1M隐藏层单元，那么一共有10^12个参数，这显然是不能接受的。（如下图所示）

但是我们在CNN里，可以大大减少参数个数，我们基于以下两个假设：

1）最底层特征都是局部性的，也就是说，我们用10x10这样大小的过滤器就能表示边缘等底层特征

2）图像上不同小片段，以及不同图像上的小片段的特征是类似的，也就是说，我们能用同样的一组分类器来描述各种各样不同的图像

基于以上两个，假设，我们就能把第一层网络结构简化如下：

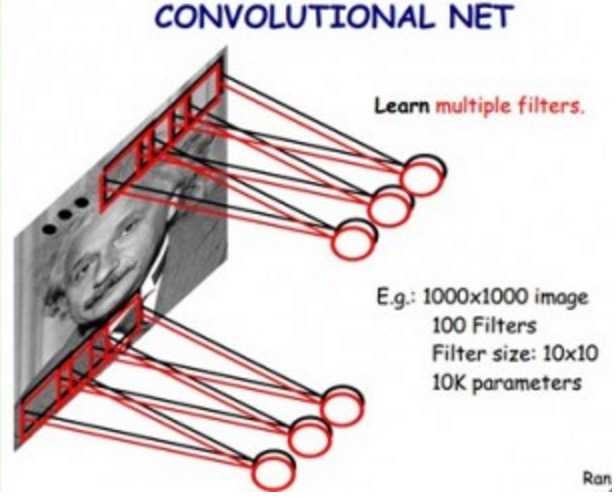
我们用100个10x10的小过滤器，就能够描述整幅图片上的底层特征。

卷积（Convolution）

卷积运算的定义如下图所示：

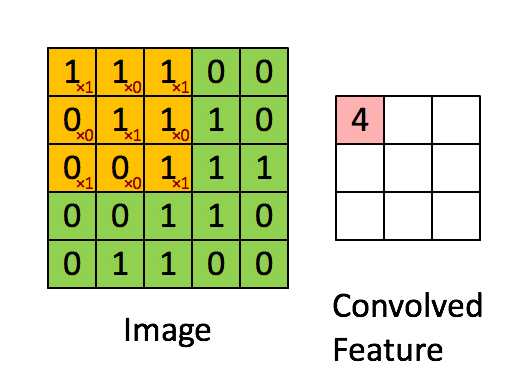
如图所示，我们有一个5x5的图像，我们用一个3x3的卷积核：

1　　0　　1

0　　1　　0

1　　0　　1

来对图像进行卷积操作（可以理解为有一个滑动窗口，把卷积核与对应的图像像素做乘积然后求和），得到了3x3的卷积结果。

这个过程我们可以理解为我们使用一个过滤器（卷积核）来过滤图像的各个小区域，从而得到这些小区域的特征值。

在实际训练过程中，卷积核的值是在学习过程中学到的。

在具体应用中，往往有多个卷积核，可以认为，每个卷积核代表了一种图像模式，如果某个图像块与此卷积核卷积出的值大，则认为此图像块十分接近于此卷积核。如果我们设计了6个卷积核，可以理解：我们认为这个图像上有6种底层纹理模式，也就是我们用6中基础模式就能描绘出一副图像。以下就是24种不同的卷积核的示例：

池化（Pooling）

池化听起来很高深，其实简单的说就是下采样。池化的过程如下图所示：

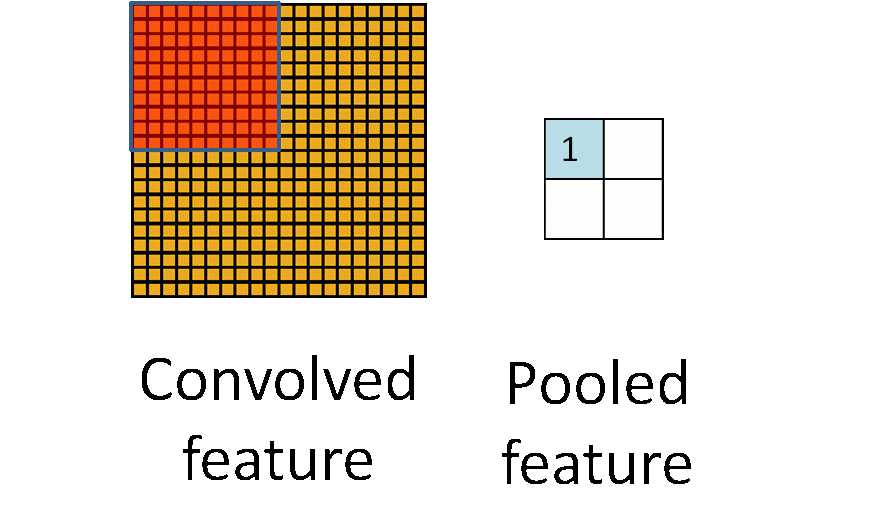
上图中，我们可以看到，原始图片是20x20的，我们对其进行下采样，采样窗口为10x10，最终将其下采样成为一个2x2大小的特征图。

之所以这么做的原因，是因为即使做完了卷积，图像仍然很大（因为卷积核比较小），所以为了降低数据维度，就进行下采样。

之所以能这么做，是因为即使减少了许多数据，特征的统计属性仍能够描述图像，而且由于降低了数据维度，有效地避免了过拟合。

在实际应用中，池化根据下采样的方法，分为最大值下采样（Max-Pooling）与平均值下采样（Mean-Pooling）。

 全连接层（fully connected layers，FC）

      在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标       记空间的作用。在实际使用中，全连接层可由卷积操作实现：对前层是全连接的全连接层可以转化为卷积核为1x1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积，h和w分别为前层卷积结果的高和宽。

全连接层的实现

LeNet介绍

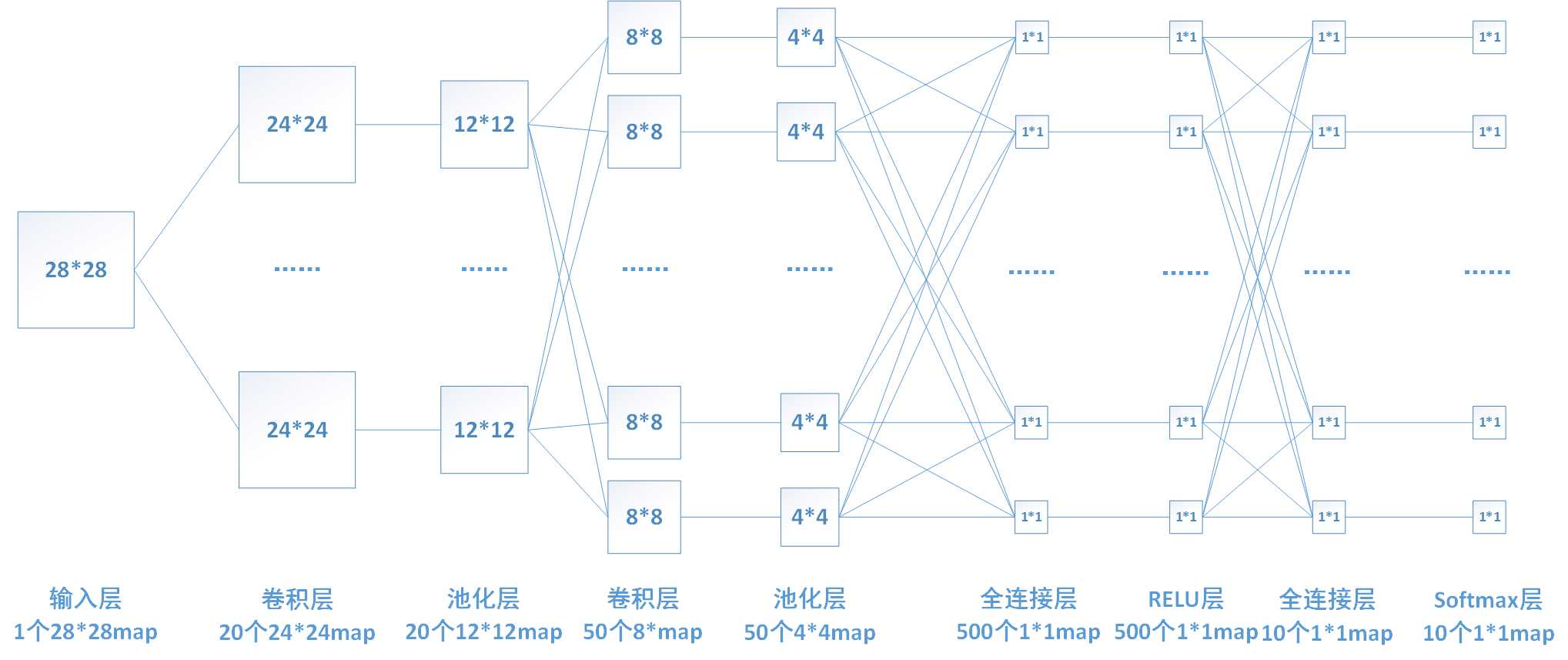
下面再回到LeNet网络结构：

这回我们就比较好理解了，原始图像进来以后，先进入一个卷积层C1，由6个5x5的卷积核组成，卷积出28x28的图像，然后下采样到14x14（S2）。

接下来，再进一个卷积层C3，由16个5x5的卷积核组成，之后再下采样到5x5（S4）。

注意，这里S2与C3的连接方式并不是全连接，而是部分连接，如下图所示：

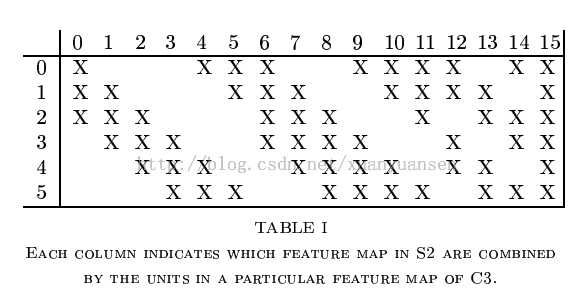
其中行代表S2层的某个节点，列代表C3层的某个节点。

我们可以看出，C3-0跟S2-0,1,2连接，C3-1跟S2-1,2,3连接，后面依次类推，仔细观察可以发现，其实就是排列组合：

0 0 0 1 1 1

0 0 1 1 1 0

0 1 1 1 0 0

...

1 1 1 1 1 1

我们可以领悟作者的意图，即用不同特征的底层组合，可以得到进一步的高级特征，例如：/ + \ = ^ （比较抽象O(∩_∩)O~），再比如好多个斜线段连成一个圆等等。

最后，通过全连接层C5、F6得到10个输出，对应10个数字的概率。

最后说一点个人的想法哈，我认为第一个卷积层选6个卷积核是有原因的，大概也许可能是因为0~9其实能用以下6个边缘来代表：

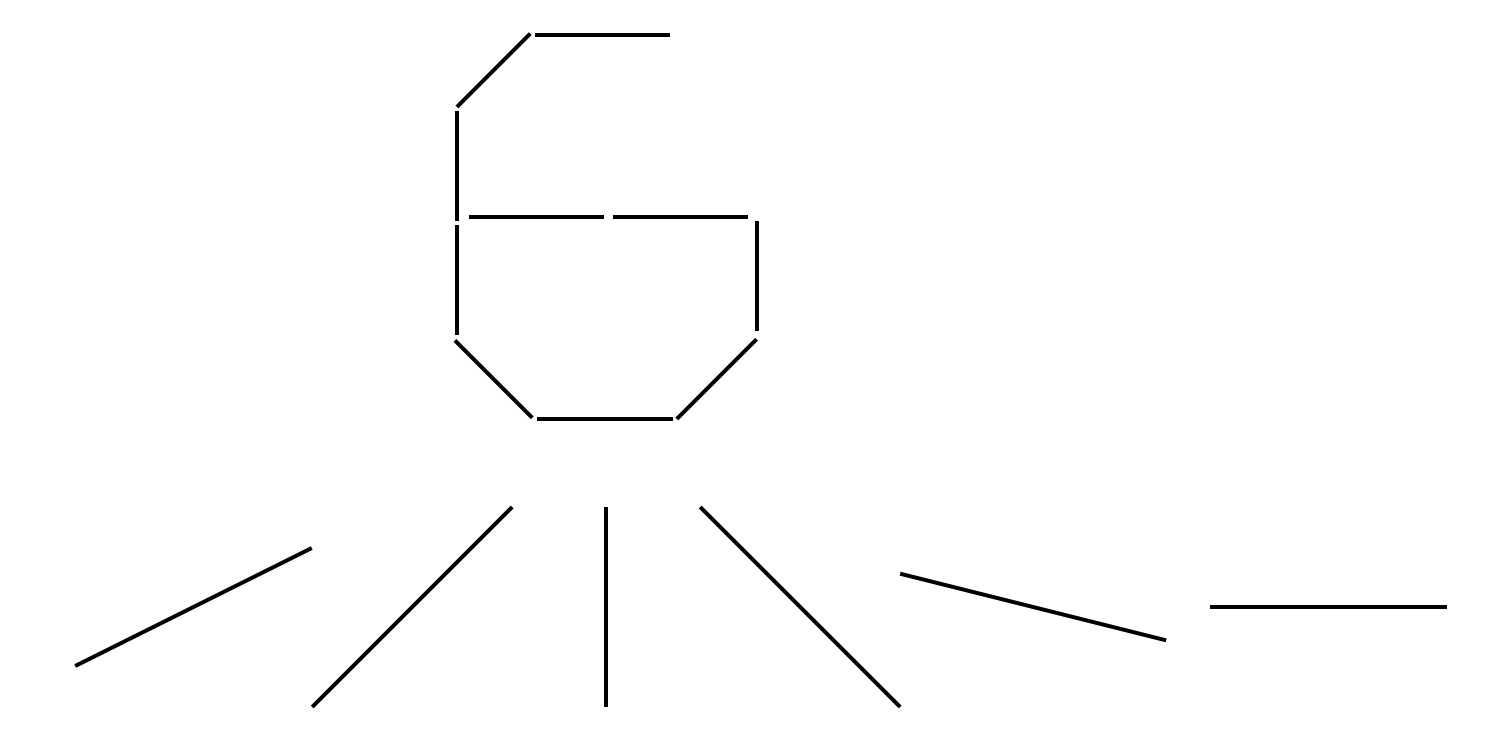
是不是有点道理呢，哈哈

然后C3层的数量选择上面也说了，是从选3个开始的排列组合，所以也是可以理解的。

其实这些都是针对特定问题的trick，现在更加通用的网络的结构都会复杂得多，至于这些网络的参数如何选择，那就需要我们好好学习了。

-----------------------------------------------------------------------------------------------------------------------

训练过程

   卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出对之间的映射能力。卷积网络执行的是有监督训练，所以其样本集是由形如：（输入向量，理想输出向量）的向量对构成的。所有这些向量对，都应该是来源于网络即将模拟的系统的实际“运行”结果。它们可以是从实际运行系统中采集来的。在开始训练前，所有的权都应该用一些不同的小随机数进行初始化。“小随机数”用来保证网络不会因权值过大而进入饱和状态，从而导致训练失败；“不同”用来保证网络可以正常地学习。实际上，如果用相同的数去初始化权矩阵，则网络无能力学习。

卷积神经网络的训练过程与传统神经网络类似，也是参照了反向传播算法。

第一阶段，向前传播阶段：

a）从样本集中取一个样本(X,Y_p)，将X输入网络；

b）计算相应的实际输出O_p。

      在此阶段，信息从输入层经过逐级的变换，传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中，网络执行的是计算（实际上就是输入与每层的权值矩阵相点乘，得到最后的输出结果）：

          O_p=F_n（…（F₂（F₁（X_pW^（1））W^（2））…）W^（n））

第二阶段，向后传播阶段

a）算实际输出O_p与相应的理想输出Y_p的差；

b）按极小化误差的方法反向传播调整权矩阵。

以上内容摘自其他博客，由于我也没有仔细了解这一块，建议直接参考原博客。

手写数字分类的例子，基于tensorflow

引自：使用TensorFlow编写识别数字的CNN训练程序详解

CNN的结构

从网上借用一张图片来表示一下，是一个有2层hidden layer的CNN。

程序中设置的一些参数是： 
卷积层1：kernel_size [5, 5], stride=1， 4个卷积窗口 
卷积层2：kernel_size [5, 5], stride=1， 6个卷积窗口 
池化层： pool_size [2, 2], stride = 2 
全连接层1: 1024个特征

MNIST数据的获取

以往我们获取MINIST的方式是:

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

现在可以： 

from tensorflow.contrib import learn
mnist = learn.datasets.load_dataset(‘mnist‘)

通过mnist.train, mnist.test, mnist.validation来获得3个数据集，每个数据集里面的方法有(已train为例)： 

• train.images 图片数据，二维数组 (55000, 784) dtype=float32 
• train.labels 图片的分类， 一维数组，每个数值表示图片对应的数字 
  array([7, 3, 4, …, 5, 6, 8], dtype=uint8)
• train.num_examples 图片数量 55000
• train.next_batch 下一批数据 
  
n = train.next_batch 
n[0] 是images n[1]是labels 


 第一次load MNIST数据的时候，会自动从网上下载，放到当前目录的MNIST-data目录下

1. 第一种加载方式，有一个one-hot参数，此时每个样本的label，返回的是一个长度10的vector，其中只有一个位置是1，其他都是0。 第二种方式，没有这个参数，如果需要的话，得直接调用datasets.mnist.read_data_sets

定义卷积层

在tf.contrib.layers里面有convolution2d，conv2d等方法，其实都是convolution方法的别名

convolution(inputs, num_outputs, kernel_size, stride=1, padding=‘SAME‘, data_format=None, rate=1, activation_fn=nn.relu, normalizer_fn=None, normalizer_params=None, weights_initializer=initializers.xavier_initializer(), weights_regularizer=None, biases_initializer=init_ops.zeros_initializer, biases_regularizer=None, reuse=None, variables_collections=None, outputs_collections=None, trainable=True, scope=None) 

这个函数很强大，1到3维的卷积都支持。(我暂时只用过2维)

• inputs: 输入变量，是一个N+2维的Tensor

  • 类型要求是一个Tensor，而我们一般训练的数据都是常量(比如mnist，load以后得到是python的数据类型，不是tf的)，所以需要把用tf的方法做一下转换，比如tf.reshape
  • 为什么是N+2维呢，比如图像，除了宽度和高度，实际上还有样本数量和通道数量(如RGB3通道)，所以多了2维。
  • inputs的格式，由date_format这个参数来觉得，比如2维，有NHWC和NCHW两种。N是样本数量，H高度，W宽度，C通道数。

• num_outputs: 卷积filter的数量，或者说提取的特征数量，比如5,10

• kernel_size: 卷积核的大小，是N个参数的list，比如二维图像，可以时候[10,10]，如果参数值相同，用一个整数来表示也可以；
• stride: 卷积步长，同样是N个参数的序列，或者都相等的话，用一个整数来表示，默认是1.
• padding: 字符串格式，默认SAME，可选’VALID’。（想问：这两个效果上有多大差异？）
• data_format: 字符串，指定inputs的格式 
  
  • 一维数据：”NWC” (default) and “NCW”
  • 二维数据：”NHWC” (default) and “NCHW”
  • 三维数据：”NDHWC”
  • 也就是，不指定的话，通道数都是最后一个参数。
• rate: a sequence of N positive integers specifying the dilation rate to use for a’trous convolution. Can be a single integer to specify the same value for all spatial dimensions. (暂时没看到其作用)
• activation_fn: 激活函数，默认relu
• normalizer_fn: normalization function to use instead of biases.（没用过，不知道起作用）
• normalizer_params： normalization function parameters.
• weights_initializer： 这不用说了，有默认值，估计用默认的就可以了。
• weights_regularizer: Optional regularizer for the weights.(没明白为什么需要这个)
• biases_initializer: 有默认值，一般也就不用指定。
• biases_regularizer: …
• reuse: whether or not the layer and its variables should be reused. To be able to reuse the layer scope must be given. 应该都需要reuse吧，所以这个参数默认为True更好，现在是None。
• variables_collections： 怎么用暂时不太明白，但应该不用指定也可以；
• outputs_collections： 同上；
• trainable： If True also add variables to the graph collection GraphKeys.TRAINABLE_VARIABLES，默认是True。 （这个是不是说在fit的时候需要设为True，evaluate和predict的时候为false？）
• scope： 也即是variable_scope， 如果用多个卷积层的话，需要设置这个参数，以便把每一次的weight和bias区别出来。

我们在对MNIST做卷积的时候，只要指定inputs, num_outputs, kernel_size, scope这几个参数就可以了，比如:

conv1 = tf.contrib.layers.conv2d(inputs, 4, [5, 5], ‘conv_layer1‘)
#stride默认1，weights和biases也都是默认的

定义池化层

可以用 tf.contrib.layers.max_pool2d或者tf.contrib.layers.avg_pool2d 

max_pool2d(inputs, kernel_size, stride=2, padding=’VALID’, data_format=DATA_FORMAT_NHWC, outputs_collections=None, scope=None)

• inputs: 就是卷积的输出了；
• kernel_size: 是不是叫pool_size更贴切。[kernel_height, kernel_width]或者是一个整数；
• stride： [stride_height, stride_width]，不过文档上说目前这两个值必须一样
• padding： 这里默认是VALID，和卷积默认不一样，为什么要这样呢？
• data_format: 注意和卷积用的一样哦；
• outputs_collections: …
• scope: pooling的时候没有参数，需要scope吗？

pool1 = tf.contrib.layers.max_pool2d(conv1, [2, 2], padding=‘SAME‘)

定义全连接层

tf.contrib.layers下有可用的全连接方法：

fully_connected(inputs, num_outputs, activation_fn=nn.relu, normalizer_fn=None, normalizer_params=None, weights_initializer=initializers.xavier_initializer(), weights_regularizer=None, biases_initializer=init_ops.zeros_initializer, biases_regularizer=None, reuse=None, variables_collections=None, outputs_collections=None, trainable=True, scope=None)

看这个函数，参数和卷积很多地方是一样的, 我们可以这样用：

fc = tf.contrib.layers.fully_connected(inputs, 1024, scope=‘fc_layer‘)

唯一需要注意的是这里的inputs参数，一般是二维的形式[batch_size, depth]，而前面卷积的结果，一般是[batch_size, height, width, channels]的形式，所以需要做一个flatten操作后再传给fully_connected。

一般在fc之后还会做dropout，可以用如下方法：

dropout(inputs, keep_prob=0.5, noise_shape=None, is_training=True, outputs_collections=None, scope=None)

参数的意义很明显，其中is_training需要注意一下，在训练的时候传True，其他情况下传False。 

dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个mini-batch都在训练不同的网络。

dropout是CNN中防止过拟合提高效果的一个大杀器。

定义logits

全连接之后，一般就是用softmax做分类，然后定义loss，就可以训练了。但是看官方的例子，softmax前还加了一步，计算叫logits的东西，代码里面的说明是：

We don’t apply softmax here because 
tf.nn.softmax_cross_entropy_with_logits accepts the unscaled logits 
and performs the softmax internally for efficiency.

为什么要这样暂时不太明白，但是依样画葫芦，定义logtis本身很简单，做一个线性变换，把FC的结果映射到分类的数量上：

def inference(x, num_class):
  with tf.variable_scope(‘softmax‘):
    dtype = x.dtype.base_dtype
    # Set up the requested initialization.
    init_mean = 0.0
    init_stddev = 0.0
    weights = tf.get_variable(‘weights‘,
                                [x.get_shape()[1], num_class], initializer=init_ops.random_normal_initializer(init_mean, init_stddev, dtype=dtype), dtype=dtype)
    biases = tf.get_variable(‘bias‘, [num_class], initializer=init_ops.random_normal_initializer(init_mean, init_stddev, dtype=dtype), dtype=dtype)

    logits = tf.nn.xw_plus_b(x, weights, biases)
    return logits

定义loss

在tf.contrib.losses下有一些预定义的loss函数，比如直接用

softmax_cross_entropy(logits, onehot_labels, weights=_WEIGHT_SENTINEL, label_smoothing=0, scope=None)

注意这里的label是onehot格式的, 我们从mnist获取的label要转换成这个格式。

定义train_op

可以用tf.contrib.layers.optimize_loss，通过传递不同的参数，就可以调用不同的优化方法。

optimize_loss(loss,
              global_step,
              learning_rate,
              optimizer,
              gradient_noise_scale=None,
              gradient_multipliers=None,
              clip_gradients=None,
              learning_rate_decay_fn=None,
              update_ops=None,
              variables=None,
              name=None,
              summaries=None,
              colocate_gradients_with_ops=False):

预定义的optimizer有：

OPTIMIZER_CLS_NAMES = {
    "Adagrad": train.AdagradOptimizer,
    "Adam": train.AdamOptimizer,
    "Ftrl": train.FtrlOptimizer,
    "Momentum": train.MomentumOptimizer,
    "RMSProp": train.RMSPropOptimizer,
    "SGD": train.GradientDescentOptimizer,
}
或者这么写
train_op = tf.contrib.layers.optimize_loss(
            loss, tf.contrib.framework.get_global_step(), optimizer=‘Adagrad‘, learning_rate=0.1)

model和Estimator

结合上面的内容，就可以定义出model， 从而用Estimator完成训练，预测等功能，完整的程序如下：

import numpy as np

import sklearn.metrics as metrics
import tensorflow as tf
from PIL import Image
from tensorflow.contrib import learn
from tensorflow.contrib.learn import SKCompat
from tensorflow.contrib.learn.python.learn.estimators import model_fn as model_fn_lib
from tensorflow.python.ops import init_ops

IMAGE_SIZE = 28
LOG_DIR = ‘./ops_logs‘

mnist = learn.datasets.load_dataset(‘mnist‘)

def inference(x, num_class):
  with tf.variable_scope(‘softmax‘):
    dtype = x.dtype.base_dtype
    init_mean = 0.0
    init_stddev = 0.0
    weight = tf.get_variable(‘weights‘,
                                [x.get_shape()[1], num_class], initializer=init_ops.random_normal_initializer(init_mean, init_stddev, dtype=dtype), dtype=dtype)
    biases = tf.get_variable(‘bias‘, [num_class], initializer=init_ops.random_normal_initializer(init_mean, init_stddev, dtype=dtype), dtype=dtype)

    logits = tf.nn.xw_plus_b(x, weight, biases)
    return logits

def model(features, labels, mode):
    if mode != model_fn_lib.ModeKeys.INFER:
        labels = tf.one_hot(labels, 10, 1, 0)
    else:
        labels = None

    inputs = tf.reshape(features, (-1, IMAGE_SIZE, IMAGE_SIZE, 1))

    #conv1
    conv1 = tf.contrib.layers.conv2d(inputs, 4, [5, 5], scope=‘conv_layer1‘, activation_fn=tf.nn.tanh);
    pool1 = tf.contrib.layers.max_pool2d(conv1, [2, 2], padding=‘SAME‘)
    #conv2
    conv2 = tf.contrib.layers.conv2d(pool1, 6, [5, 5], scope=‘conv_layer2‘, activation_fn=tf.nn.tanh);
    pool2 = tf.contrib.layers.max_pool2d(conv2, [2, 2], padding=‘SAME‘)
    pool2_shape = pool2.get_shape()
    pool2_in_flat = tf.reshape(pool2, [pool2_shape[0].value or -1, np.prod(pool2_shape[1:]).value])
    #fc
    fc1 = tf.contrib.layers.fully_connected(pool2_in_flat, 1024, scope=‘fc_layer1‘, activation_fn=tf.nn.tanh)
    #dropout
    is_training = False
    if mode == model_fn_lib.ModeKeys.TRAIN:
        is_training = True

    dropout = tf.contrib.layers.dropout(fc1, keep_prob=0.5, is_training=is_training, scope=‘dropout‘)

    logits = inference(dropout, 10)
    prediction = tf.nn.softmax(logits)
    if mode != model_fn_lib.ModeKeys.INFER:
        loss = tf.contrib.losses.softmax_cross_entropy(logits, labels)
        train_op = tf.contrib.layers.optimize_loss(
            loss, tf.contrib.framework.get_global_step(), optimizer=‘Adagrad‘,
            learning_rate=0.1)
    else:
        train_op = None
        loss = None

    return {‘class‘: tf.argmax(prediction, 1), ‘prob‘: prediction}, loss, train_op


classifier = SKCompat(learn.Estimator(model_fn=model, model_dir=LOG_DIR))

classifier.fit(mnist.train.images, mnist.train.labels, steps=1000, batch_size=300)

predictions = classifier.predict(mnist.test.images)
score = metrics.accuracy_score(mnist.test.labels, predictions[‘class‘])
print(‘Accuracy: {0:f}‘.format(score))

深度学习基础（CNN详解以及训练过程1）

标签：instead   维度   接下来   目录   request   argmax   tail   ges   pytho   

原文地址：https://www.cnblogs.com/Anita9002/p/9296014.html