UVA10566 Crossed Ladders

Description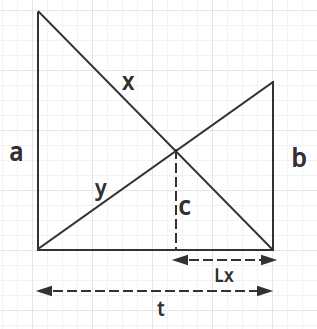

如图1,多组数据,输入x,y,c,求出t的大小,保留三位小数

Hint
由相似三角形的知识,我们用两种方法分别表示出图中Lx,就可以得出一个等式关系:$$\frac{1}{b}+\frac{1}{a}=\frac{1}{c}
??(1)$$
又有等式$$a=\sqrt{x^2-t^2}
,
b=\sqrt{y^2-t^2}$$
把这两式代入(1)式可以得到$$\frac{1}{\sqrt{x^2-t^2}}+\frac{1}{\sqrt{y^2-t^2}}=\frac{1}{c}$$
我们并不需要把它解出来
可以发现左边的式子关于t是单调的,所以我们二分t即可

Code

#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define siz 
#define minn(a,b) (a<b?a:b)
using namespace std;
double x, y, c;
double work(double t) {
    return 1 / sqrt(x * x - t * t) + 1 / sqrt(y * y - t * t);
}
int main() {

    while( ~scanf("%lf%lf%lf",&x,&y,&c) ) {
        double l = 0, r = minn(x,y), mid;
        while(r - l > 1e-5) {
            mid = l + (r - l) / 2; 
            if( work(mid) > (1/c) ) r=mid;
            else l=mid;
        }
        printf("%.3lf\n",mid);
    }
    return 0;
}

Tips

• mid = l + (r - l) / 2; 之所以这样求mid,是怕有恶心数据让(l+r)越界
• (r-l)>>1 是错误的! double是不能使用右移运算的