P1268 树的重量

标签：.com   info   包含   style   namespace   --   its   ++   ret   

题目描述

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令N={1..n}，用一个N上的矩阵M来定义树T。其中，矩阵M满足：对于任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。树T满足：

1．叶节点属于集合N；

2．边权均为非负整数；

3．dT(i,j)=M[i,j]，其中dT(i,j)表示树上i到j的最短路径长度。

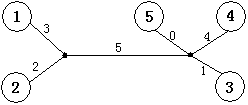
如下图，矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵M。你的任务就是，根据给出的矩阵M，计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树，这棵树的总重量为15。

输入输出格式

输入格式：

输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行，给出的是矩阵M的一个上三角(不包含对角线)，矩阵中所有元素是不超过100的非负整数。输入数据保证合法。

输入数据以n=0结尾。

输出格式：

对于每组输入，输出一行，一个整数，表示树的重量。

输入输出样例

5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0

15
71

Solution：

　　本题很有意思的思维题（话说期末考崩了啊，本来想数学拉分的，结果数学也炸了，好崩心态啊！滚粗搞竞赛！）。

　　题意等价于给定一棵树的$n$个叶子节点之间的最短路径，且$d[i][j]+d[j][k]\geq d[i][k]$，需要求出满足条件的树的边权和（我们不必在乎点具体所在位置，只需考虑长度的贡献）。

　　首先不难想到的是当只有两个叶子节点时，显然答案为$d[1][2]$。

　　而当$n==3$时，因为要满足标号节点均为叶子节点，所以多出的$3$号叶子节点必定只能由$G[1][2]$之间多出一条分枝相连，如图：

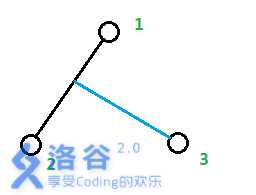
　　那么多出的分枝长度显然为$\frac{d[1][3]+d[2][3]-d[1][2]}{2}$。

　　当$n==4$时，还是得满足均为叶子节点的限制，所以多出的节点显然只能在$G[1][2]$或$G[1][3]$或$G[2][3]$这三条分枝上再接一条分枝与$4$相连，如图：

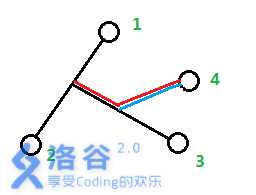
　　容易发现，此时多出的长度为$min(\frac{d[1][4]+d[2][4]-d[1][2]}{2},\frac{d[1][4]+d[3][4]-d[1][3]}{2},\frac{d[2][3]+d[3][4]-d[2][4]}{2})$。

　　不难发现每次多出的$n$号节点，需要枚举在前$n-1$个节点互相之间的路径上多出分枝的情况，取最小值累加。

　　那么实现时直接模拟就好了。

代码：

 1 #include<bits/stdc++.h>
 2 #define il inline
 3 #define ll long long
 4 #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
 5 #define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
 6 using namespace std;
 7 int n,mp[31][31],ans,tp;
 8 
 9 il int gi(){
10     int a=0;char x=getchar();
11     while(x<‘0‘||x>‘9‘)x=getchar();
12     while(x>=‘0‘&&x<=‘9‘)a=(a<<3)+(a<<1)+x-48,x=getchar();
13     return a;
14 }
15 
16 int main(){
17     while(scanf("%d",&n)!=EOF&&n){
18         For(i,1,n-1) For(j,i+1,n) mp[i][j]=mp[j][i]=gi();
19         ans=mp[1][2];
20         For(i,3,n){
21             tp=0x7fffffff;
22             For(j,1,i-1) For(k,1,j-1)
23                 tp=min(tp,(mp[j][i]+mp[k][i]-mp[j][k])>>1);
24             ans+=tp;
25         }
26         printf("%d\n",ans);
27     }
28     return 0;
29 }

P1268 树的重量

标签：.com   info   包含   style   namespace   --   its   ++   ret   

原文地址：https://www.cnblogs.com/five20/p/9302113.html