标签:问题 lse 注意 动态 upd 直接 [1] 第一条 php
哇我感觉这题真的qwq是很好的一题呀qwq
很神qwq反正我真的是自己想怎么想都想不到就是了qwq
首先先考虑一下简化版的问题应该怎么解决:
1、如果说我知道\(x_1\equiv k_1*x_2+b_1(mod\ 10007)\),并且\(x_2\)已知,那么显然有当\(k_1=0\)时有\(x_1=x_2\);\(k_1=1\)且\(b_1=0\)时有无数组解,\(k_1=1\)且\(b_1\)不为\(0\)时无解;\(k_1>1\)时逆元求解(因为\(10007\)是质数嘛)
2、如果说我知道\(x_1\equiv k_1*x_2+b_1(mod\ 10007)\)和\(x_2\equiv k_2*x_1+b_1(mod \ 10007)\),那么怎么求\(x_1\)呢
有一种很粗暴的方法就是直接把第一条式子中的\(x_2\)用第二条式子的右边部分替换掉,然后直接解
?
然后我们可以想办法往这个方向靠
我们来小小的转化一下这个问题,我们考虑把每一条式子\(x_i=k_i*x_{p_i}+b_i\),转化为由\(x_{p_i}\)向\(x_i\)连一条有向边,然后这样的话我们就可以得到一个。。基环外向树森林,大概是若干个长这个样子的东西(额当然这里没有把边的方向画出来):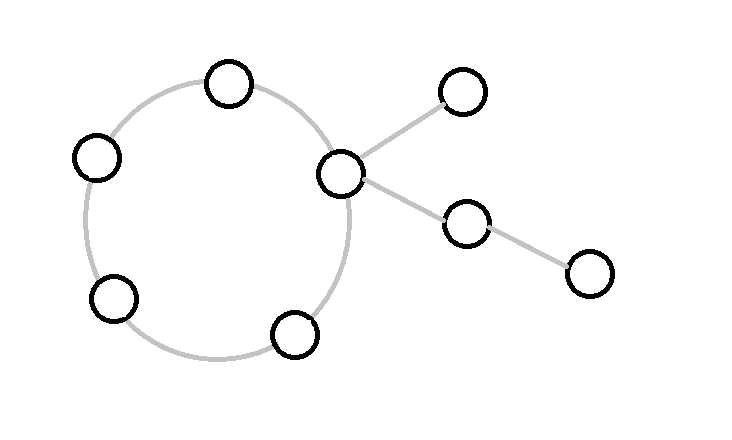
处理这样的东西,有一个比较套路的方法就是拆掉环上一条边然后变成树来维护处理
我们选环上的其中一个点作为这块东西的\(rt\),然后将拆掉的那条边(某个点\(y\)指到\(rt\))对应的点\(y\)记为\(sp[rt]\),也就是\(rt\)的一个\(special\ father\)
然后我们考虑用LCT来维护这个东西,但是具体维护什么呢
这里有一个很神的想法,对于每一个splay上的节点,我们维护其子树内最左边的节点\(L\)(也就是深度最浅的那个)的\(sp\)表达最右边的那个节点\(R\)(深度最深的那个)的表达式的两个系数,也就是:
\[
x_{R}=k*x_L+b
\]
对于splay上的每个节点我们维护上面这个式子里面的\(k\)和\(b\)分别是多少(记作\(info[x].k\)和\(info[x].b\))
这样一来,我们对于一个节点\(x_i\)做了\(access(x_i)\)以及\(splay(x_i)\)之后,\(info[x]\)中存的表达式其实就是:
\[
x_i=k*sp[rt]+b
\]
那么对于每次查询(记查询的那个点为\(x_a\)),我们需要做的就是用上面的操作得到\(x_i\)和\(sp[rt]\)之间的表达式,然后只要再得到\(sp[rt]\)关于自己的表达式我们就可以求出\(sp[rt]\)进而求得\(x_i\)了。后者的话因为根据定义\(sp[rt]\)应该是这棵树中的某个节点,所以我们直接用同样的\(access+splay\)操作就可以得到\(sp[rt]\)关于自己的表达式了
然后对于修改的话,我们需要分类讨论一下(可以自己画个图理解一下就很清晰了)
1、\(rt=x\)
? 这里又可以再分两类
? 如果说\(p\)在这棵树中,那么修改\(sp[rt]\)即可;否则\(sp[rt]=0\)然后将\(rt\)接到\(p\)这个节点上面去,作为\(p\)的一个儿子
2、\(rt!=x\)
不管别的首先我们都要将\(x\)和原来的\(fa[x]\)断开
? 如果说\(x\)在\(rt\)到\(sp[rt]\)的这个环上的话,断开之后会有一个影响,就是\(sp[rt]\)指向\(rt\)这条边不需要断开了,所以我们要将\(rt\)连到\(sp[rt]\)那里去作为其一个儿子
然后不管是\(x\)是否在环上,我们都要判断如果说\(p\)在这棵树上,那么\(sp[x]=p\),否则\(sp[x]=0\)然后将\(x\)连到\(p\)那里去作为其一个儿子
? 这些都讨论完了之后,我们来想想这个关键的\(info[x]\)要怎么维护
注意到这个在\(update\)的时候是必须按照一定顺序的,因为一个节点\(x\)的信息只能和原树中的\(fa[x]\)合并
具体一点就是:
\[
\begin{aligned}
x&=k_1*x_{fa}+b_1\x_{fa}&=k_2*x'+b_2\\\downarrow\\x&=k_1(k_2*x'+b_2)+b_1
\end{aligned}
\]
我们用\(ch[x][0]\)和\(ch[x][1]\)表示splay中\(x\)节点的左右儿子
? 假设我们现在知道\(info[ch[x][0]]]\)和\(info[ch[x][1]]\),我们想要得到\(info[x]\),那么其实只要先将\(info[ch[x][0]]\)表示的式子和\(x\)本身的式子先合并存为\(info[x]\),再将\(info[x]\)与\(info[ch[x][1]]\)合并即可,具体的话就是因为左子树中深度最深的节点在原树上就是\(fa[x]\),同理右子树中深度最浅的节点在原树上的\(fa\)就是\(x\),所以直接这么合并就好了
想明白了的话还是挺好写的ovo(废话qwq然而我想了一天。。。)
?
代码大概长这个样子
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=30010,MOD=10007,LCT=N;
struct Data{
int k,b;
Data(){}
Data(int k1,int b1){k=k1; b=b1;}
friend Data operator + (Data x,Data y)
{return Data(x.k*y.k%MOD,(x.b*y.k%MOD+y.b)%MOD);}
}val[N];
int h[N],vis[N],Fa[N],inv[N];
int n,m,tot,Cnt;
namespace Lct{/*{{{*/
int ch[LCT][10],fa[LCT],sp[LCT];
Data info[LCT];
int tot;
bool isroot(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
int which(int x){return ch[fa[x]][1]==x;}
void update(int x){//order is important
info[x]=val[x];
if (ch[x][0]) info[x]=info[ch[x][0]]+info[x];
if (ch[x][1]) info[x]=info[x]+info[ch[x][1]];
}
void rotate(int x){
int dir=which(x),f=fa[x];
if (!isroot(f)) ch[fa[f]][which(f)]=x;
fa[x]=fa[f]; fa[f]=x;
if (ch[x][dir^1]) fa[ch[x][dir^1]]=f;
ch[f][dir]=ch[x][dir^1];
ch[x][dir^1]=f;
update(f); update(x);
}
void splay(int x){
for (int f=fa[x];!isroot(x);f=fa[x]){
if (!isroot(f))
rotate(which(f)==which(x)?f:x);
rotate(x);
}
}
void access(int x){
for (int last=0;x;last=x,x=fa[x]){
splay(x);
ch[x][1]=last;
update(x);
}
}
int get_rt(int x){
access(x); splay(x);
while (ch[x][0]) x=ch[x][0];
return x;
}
void query(int x){
Data tmp1,tmp2;
access(x); splay(x);
tmp1=info[x];//sp[rt]-->x
int rt=get_rt(x);
access(sp[rt]); splay(sp[rt]);
tmp2=info[sp[rt]];//sp[rt]-->sp[rt]
if (tmp2.k==1){
if (tmp2.b==0) printf("-2\n");
else printf("-1\n");
}
else{
int valrt=inv[(1-tmp2.k+MOD)%MOD]*tmp2.b%MOD;
printf("%d\n",(tmp1.k*valrt%MOD+tmp1.b)%MOD);
}
}
void Cut(int x){
access(x); splay(x);
ch[x][0]=fa[ch[x][0]]=0;
update(x);
}
bool InCir(int x,int y){//x in cir(y,sp[y])?
access(sp[y]);
splay(sp[y]);
splay(x);
return x==sp[y]||(!isroot(sp[y]));
}
void change(int x,int k,int p,int b){
access(x);
splay(x);
val[x]=Data(k,b);
update(x);
int rt=get_rt(x);
if (rt==x){
if (get_rt(p)==rt) sp[x]=p;
else sp[rt]=0,fa[rt]=p;
}
else{
if (InCir(x,rt)){
Cut(x);
splay(rt);
fa[rt]=sp[rt];
sp[rt]=0;
}
else
Cut(x);
if (get_rt(p)==x)
sp[x]=p;
else
sp[x]=0,fa[x]=p;
}
}
}/*}}}*/
void prework(int x){
vis[x]=Cnt;
Lct::fa[x]=Fa[x];
if (vis[Fa[x]]==Cnt){
Lct::fa[x]=0;
Lct::sp[x]=Fa[x];
return;
}
prework(Fa[x]);
}
void get_inv(int n){
inv[1]=1;
for (int i=2;i<=n;++i)
inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD;
};
int main(){/*{{{*/
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
#endif
char op[5];
int x,p,k,b;
scanf("%d",&n);
for (int i=1;i<=n;++i)
scanf("%d%d%d",&val[i].k,&Fa[i],&val[i].b);
get_inv(N-10);
Cnt=0;
for (int i=1;i<=n;++i)
if (!vis[i])
++Cnt,prework(i);
scanf("%d",&m);
for (int i=1;i<=m;++i){
scanf("%s",op);
if (op[0]=='A'){
scanf("%d",&x);
Lct::query(x);
}
else{
scanf("%d%d%d%d%d",&x,&k,&p,&b);
Lct::change(x,k,p,b);
}
}
}/*}}}*/标签:问题 lse 注意 动态 upd 直接 [1] 第一条 php
原文地址:https://www.cnblogs.com/yoyoball/p/9311127.html