标签:条件 clu cer blank 影响 输入 证明 技术分享 tle
这次练习,感觉自己存在很多细节的问题。

比如,前3个题很搞笑,被罚了4次时(A题是写了假贪心,B题是忘了条件,C题是忽略细节)。同时时间也安排的不是很好,比如F题的代码很长,但是我先去写了F,再去写G题,到时Penalty再度变高。
还有件有趣的事,切完D题,输地址时输成了F题(大概是我字母表背得有点"好"),成功跳过E题。
最后看E题,没仔细看读入,发现样例有毒,手算始终不对。时间再度-10min。
最后比较悲催的是H和I根本没时间看。虽然估计看了也做不起。
唯一感到比较欣慰的是多年做cf的题,英语水平有提升(大概是一场比赛题面的单词本来就不多),基本不用翻译就能读懂题目。
题目大意
给定一个只包含‘L‘和‘R‘的字符串,你可以将"LR"或者‘RL"替换为"D"。问能使串长能变成的最小值。
最开始感觉可以贪心。然后:

改成dp,成功AC。(为什么A题会是dp,没道理啊。。)

1 /** 2 * Codeforces 3 * Problem#954A 4 * Accepted 5 * Time: 31ms 6 * Memory: 0k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int inf = 2000; 13 14 int n; 15 char str[105]; 16 int f[105][2]; 17 18 inline void init() { 19 scanf("%d", &n); 20 scanf("%s", str); 21 } 22 23 inline void solve() { 24 f[0][0] = 1, f[0][1] = inf; 25 for (int i = 1; i < n; i++) { 26 if (str[i] != str[i - 1]) 27 f[i][1] = f[i - 1][0]; 28 else 29 f[i][1] = inf; 30 f[i][0] = min(f[i - 1][1], f[i - 1][0]) + 1; 31 } 32 printf("%d", min(f[n - 1][0], f[n - 1][1])); 33 } 34 35 int main() { 36 init(); 37 solve(); 38 return 0; 39 }
题目大意
有一台打字机,要输入1个字符串,有两种操作:
操作2只能使用1次。问最少的操作次数。
没看到只能用1次,傻傻地写了个dp。并成功获得了:

然后急急忙忙去加个状态。
其实只能用1次直接贪心就好了。当减少的操作次数最多的时候用操作2.

1 /** 2 * Codeforces 3 * Problem#954B 4 * Accepted 5 * Time: 31ms 6 * Memory: 0k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n; 13 char str[105]; 14 int f[105][2]; 15 16 inline void init() { 17 scanf("%d", &n); 18 scanf("%s", str + 1); 19 } 20 21 boolean equal(int l1, int l2, int len) { 22 for (int i = 0; i < len; i++) 23 if (str[l1 + i] != str[l2 + i]) 24 return false; 25 return true; 26 } 27 28 inline void solve() { 29 f[0][1] = 2000; 30 for (int i = 1; i <= n; i++) { 31 f[i][0] = f[i - 1][0] + 1; 32 f[i][1] = f[i - 1][1] + 1; 33 if (!(i & 1) && (equal(1, (i >> 1) + 1, i >> 1))) 34 f[i][1] = min(f[i][1], f[i >> 1][0] + 1); 35 } 36 printf("%d\n", min(f[n][0], f[n][1])); 37 } 38 39 int main() { 40 init(); 41 solve(); 42 return 0; 43 }
题目大意
有一个$x\times y$的网格图,但是不知道$x, y$的值。规定$i$行$j$列的格子的标号为$(i - 1)y + j$。
给定一个长度为$n$的经过的格子序列,规定只能走相邻的格子,且不能走出边界,也不能停留在同一个格子。问是否可能存在一组$x, y$使得路径合法,如果存在,输出这一组。
找最大的一组相邻的差作为$y$。
$x$足够大就好了(为什么?因为没影响)。
然后代进去检验是否合法。

1 /** 2 * Codeforces 3 * Problem#954C 4 * Accepted 5 * Time: 61ms 6 * Memory: 800k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n; 13 int *ar; 14 15 inline void init() { 16 scanf("%d", &n); 17 ar = new int[(n + 1)]; 18 for (int i = 1; i <= n; i++) 19 scanf("%d", ar + i); 20 } 21 22 int mxd = 1; 23 set<int> s; 24 void termin() { 25 puts("NO"); 26 exit(0); 27 } 28 29 inline void solve() { 30 for (int i = 1; i < n; i++) { 31 int dif = abs(ar[i + 1] - ar[i]); 32 if (!dif) 33 termin(); 34 if (mxd > 1 && dif > 1 && dif != mxd) 35 termin(); 36 if (dif > 1) 37 mxd = dif; 38 } 39 40 int ly = ar[1] % mxd; 41 if (!ly) ly = mxd; 42 int lx = (ar[1] - ly) / mxd + 1; 43 for (int i = 2, cx, cy; i <= n; i++) { 44 cy = ar[i] % mxd; 45 if (!cy) cy = mxd; 46 cx = (ar[i] - cy) / mxd + 1; 47 if (abs(cx - lx) + abs(cy - ly) != 1) 48 termin(); 49 lx = cx, ly = cy; 50 } 51 puts("YES"); 52 printf("%d %d", 1000000000, mxd); 53 } 54 55 int main() { 56 init(); 57 solve(); 58 return 0; 59 }
题目大意
给定$n$个点$m$条边的无向连通简单图。每条边边权均为1。
要求加一条原本不存在的边,使得新图没有自环,$s, t$之间的距离不改变。
问方案数。
看这数据范围挺小的。
分别跑出$s, t$的最短路径生成树。
然后枚举边的两个端点,判断加入后新产生的路径长度是否合法。

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef bool boolean; 4 5 const int N = 1e3 + 5; 6 7 int n, m, s, t; 8 boolean g[N][N]; 9 int f1[N], f2[N]; 10 11 inline void init() { 12 scanf("%d%d%d%d", &n, &m, &s, &t); 13 for (int i = 1, u, v; i <= m; i++) { 14 scanf("%d%d", &u, &v); 15 g[u][v] = true, g[v][u] = true; 16 } 17 } 18 19 typedef class Node { 20 public: 21 int p, dis; 22 23 Node(int p = 0, int dis = 0):p(p), dis(dis) { } 24 25 boolean operator < (Node b) const { 26 return dis > b.dis; 27 } 28 }Node; 29 30 priority_queue<Node> que; 31 void dijstra(int s, int* f) { 32 memset(f, 0x7f, sizeof(int) * (n + 1)); 33 que.push(Node(s, f[s] = 0)); 34 while (!que.empty()) { 35 Node e = que.top(); 36 que.pop(); 37 if (e.dis != f[e.p]) 38 continue; 39 for (int i = 1; i <= n; i++) 40 if (g[e.p][i] && e.dis + 1 < f[i]) 41 que.push(Node(i, f[i] = e.dis + 1)); 42 } 43 } 44 45 int ans = 0; 46 inline void solve() { 47 dijstra(s, f1); 48 dijstra(t, f2); 49 for (int i = 1; i <= n; i++) 50 for (int j = i + 1; j <= n; j++) 51 if (!g[i][j] && f1[i] + f2[j] + 1 >= f1[t] && f1[j] + f2[i] + 1 >= f1[t]) 52 ans++; 53 printf("%d", ans); 54 } 55 56 int main() { 57 init(); 58 solve(); 59 return 0; 60 }
题目大意
给定$n, T, a_{i}, t_{i}$,找出一组$x_{i}$满足$0\leqslant x_{i} \leqslant a_{i}$,且$\frac{\sum_{i = 1}^{n}x_{i}t_{i}}{\sum_{i = 1}^{n}x_{i}} = T$。问$\sum_{i = 1}^{n}x_{i}$的最大值。无解输出0。
好像一群人直接贪心。表示考场上没想出纯贪心。
Virtual Contest中看完题,觉得可以用函数搞一搞。
考虑如果设$D = \sum_{i = 1}^{n}x_{i}$,那么设$f(D), g(D)$分别是$\sum_{i = 1}^{n}x_{i}t_{i}$的最小值和最大值。
然后猜想$[f(D), g(D)]$之间的一切实数都可以被$\sum_{i = 1}^{n}x_{i}t_{i}$凑出来。
然后表示智商不够,不会证明。日后会了补上。
至于$f(D), g(D)$显然可以用贪心来求。画出来的图像大概是这样的:
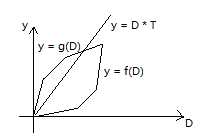
当$y = T\times D$被另两函数夹在中间的时候都是合法的。因此我们可以求在第一象限内的两个交点。求出来之后就可以算答案了。
于是便有了二分答案 + 贪心的做法。然后我也不知道发生了什么:

然后我改成函数求交:

有毒。

1 /** 2 * Codeforces 3 * Problem#954E 4 * Accepted 5 * Time: 109ms 6 * Memory: 1600k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int N = 2e5 + 5; 13 14 typedef class Tap { 15 public: 16 int a, t; 17 18 boolean operator < (Tap b) const { 19 return t < b.t; 20 } 21 }Tap; 22 23 int n, T; 24 Tap ts[N]; 25 double s = 0, sT = 0; 26 27 inline void init() { 28 scanf("%d%d", &n, &T); 29 for (int i = 1; i <= n; i++) 30 scanf("%d", &ts[i].a); 31 for (int i = 1; i <= n; i++) 32 scanf("%d", &ts[i].t); 33 for (int i = 1; i <= n; i++) { 34 if (ts[i].t != T) 35 s += ts[i].a; 36 else 37 sT += ts[i].a; 38 } 39 } 40 41 inline void solve() { 42 sort(ts + 1, ts + n + 1); 43 44 if (ts[1].t > T || ts[n].t < T) { 45 puts("0"); 46 return; 47 } 48 49 double sm = 0, sa = 0; 50 double l = 0, r = 0; 51 for (int i = 1; i <= n; i++) { 52 if (ts[i].t == T) 53 continue; 54 if ((sa + ts[i].a) * T > sm + ts[i].a * 1ll * ts[i].t) 55 sa += ts[i].a, sm += ts[i].a * 1ll * ts[i].t, l = sa; 56 else { 57 double dis = sa * T - sm; 58 double dx = dis / (ts[i].t - T); 59 l = sa + dx; 60 break; 61 } 62 } 63 64 sm = 0, sa = 0; 65 for (int i = n; i; i--) { 66 if (ts[i].t == T) 67 continue; 68 if ((sa + ts[i].a) * T < sm + ts[i].a * 1ll * ts[i].t) 69 sa += ts[i].a, sm += ts[i].a * 1ll * ts[i].t, r = sa; 70 else { 71 double dis = sa * T - sm; 72 double dx = dis / (ts[i].t - T); 73 r = sa + dx; 74 } 75 } 76 77 printf("%.9lf", min(l, r) + sT); 78 } 79 80 int main() { 81 init(); 82 solve(); 83 return 0; 84 }
题目大意
给定一个$3\times m$的棋盘,在$(2, 1)$的地方有一个棋子,棋子每次只能移动到下一列的相邻的行或者当前行。
棋盘上有$n$段障碍,第$i$段障碍是在第$a_{i}$行的$l_{i}$列到第$r_{i}$列。棋子不能到障碍格上。
问棋子从$(2, 1)$到$(2, m)$的方案数。(答案模$10^{9} + 7$)
随便写写dp方程,把转移表变成矩阵。跑快速幂。

1 /** 2 * Codeforces 3 * Problem#954F 4 * Accepted 5 * Time: 390ms 6 * Memory: 1700k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 17 #define ll long long 18 #define pli pair<ll, int> 19 20 typedef class Segment { 21 public: 22 ll l, r; 23 int sta; 24 25 Segment() { } 26 Segment(ll l, ll r, int sta):l(l), r(r), sta(sta) { } 27 }Segment; 28 29 const int M = 1e9 + 7; 30 31 typedef class Matrix { 32 public: 33 int r, c; 34 int a[3][3]; 35 36 Matrix(int r = 0, int c = 0):r(r), c(c) {} 37 38 Matrix operator * (Matrix b) { 39 Matrix rt(r, b.c); 40 assert(c == b.r); 41 for (int i = 0; i < r; i++) 42 for (int j = 0; j < b.c; j++) { 43 rt[i][j] = 0; 44 for (int k = 0; k < c; k++) 45 rt[i][j] = (rt[i][j] + a[i][k] * 1ll * b[k][j]) % M; 46 } 47 return rt; 48 } 49 50 int* operator [] (int p) { 51 return a[p]; 52 } 53 }Matrix; 54 55 const int N = 3e4 + 6; 56 57 Matrix qpow(Matrix a, ll p) { 58 assert(p >= 0); 59 Matrix pa = a, rt(3, 3); 60 for (int i = 0; i < 3; i++) 61 for (int j = 0; j < 3; j++) 62 rt[i][j] = (i == j); 63 for ( ; p; p >>= 1, pa = pa * pa) 64 if (p & 1) 65 rt = rt * pa; 66 return rt; 67 } 68 69 int n; 70 ll m; 71 pli ad[N], rm[N]; 72 Segment ss[N]; 73 74 inline void init() { 75 scanf("%d"Auto, &n, &m); 76 int a; 77 ll l, r; 78 for (int i = 1; i <= n; i++) { 79 scanf("%d"Auto""Auto, &a, &l, &r); 80 ad[i].first = l, ad[i].second = a - 1; 81 rm[i].first = r + 1, rm[i].second = a - 1; 82 } 83 } 84 85 Matrix mktrans(int os, int ns) { 86 Matrix rt(3, 3); 87 for (int i = 0; i < 3; i++) 88 for (int j = 0; j < 3; j++) 89 rt[i][j] = (abs(i - j) <= 1 && !(os & (1 << i)) && !(ns & (1 << j))); 90 return rt; 91 } 92 93 int ts[4], tp = 0; 94 inline void solve() { 95 sort(ad + 1, ad + n + 1); 96 sort(rm + 1, rm + n + 1); 97 int ca = 1, cb = 1; 98 ll st = 1, ed; 99 while (ca <= n || cb <= n) { 100 while (ca <= n && ad[ca].first == st) 101 ts[ad[ca].second]++, ca++; 102 while (cb <= n && rm[cb].first == st) 103 ts[rm[cb].second]--, cb++; 104 105 int sta = 0; 106 for (int i = 0; i < 3; i++) 107 if (ts[i]) 108 sta |= (1 << i); 109 110 ed = m + 1; 111 if (ca <= n) 112 ed = ad[ca].first; 113 if (cb <= n) 114 ed = min(ed, rm[cb].first); 115 ss[++tp] = Segment(st, ed - 1, sta); 116 st = ed; 117 } 118 119 Matrix f(1, 3); 120 f[0][0] = f[0][2] = 0, f[0][1] = 1; 121 Matrix T = mktrans(ss[1].sta, ss[1].sta); 122 f = f * qpow(T, ss[1].r - ss[1].l); 123 // cerr << f[0][0] << " " << f[0][1] << " " << f[0][2] << endl; 124 for (int i = 2; i <= tp; i++) { 125 T = mktrans(ss[i - 1].sta, ss[i].sta); 126 f = f * T; 127 T = mktrans(ss[i].sta, ss[i].sta); 128 f = f * qpow(T, ss[i].r - ss[i].l); 129 // cerr << ss[i].l << " " << ss[i].r << endl; 130 // cerr << f[0][0] << " " << f[0][1] << " " << f[0][2] << endl; 131 } 132 printf("%d\n", f[0][1]); 133 } 134 135 int main() { 136 init(); 137 solve(); 138 return 0; 139 }
题目大意
有片城墙被分为$n$个防守段。第$i$段有$a_{i}$个弓箭手。定义一段防守段的防御力是距离它的距离不超过$r$的所有防守段的弓箭手数量之和。定义这片城墙的稳定程度是每个防守段的防御力的最小值。
现在有$k$个后备弓箭手,你可将他们分配任何防守段,但不能调动原有的弓箭手。问调动后最大的稳定程度。
显然二分答案。
考虑怎么check。对于一个防御值小于$mid$的防守段$i$,能对它产生贡献的一些防守段中分配的后备弓箭手总数不得小于$mid - def[i[$。
然后设在第$i$个防守段设置的弓箭手数量为$a_{i}$,对它求一个前缀和$s$。
显然使用差分约束,然后连边就很显然了:
由于图比较特殊,不必用最短路算法。直接一个for,完事。
(感觉把防守段替换为烽火台食用更佳,总之原题说的是section,是在不知道怎么翻译比较好)。

1 /** 2 * Codeforces 3 * Problem#954G 4 * Accepted 5 * Time: 358ms 6 * Memory: 13700k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 17 #define ll long long 18 19 const int N = 5e5 + 5; 20 21 int n, r; 22 ll k; 23 int ar[N]; 24 ll ps[N], def[N]; 25 ll f[N]; 26 27 inline void init() { 28 scanf("%d%d"Auto, &n, &r, &k); 29 for (int i = 1; i <= n; i++) 30 scanf("%d", ar + i); 31 for (int i = 1; i <= n; i++) 32 ps[i] = ps[i - 1] + ar[i]; 33 } 34 35 boolean check(ll mid) { 36 memset(f, 0, sizeof(f)); 37 for (int i = 1; i <= n; i++) { 38 f[i] = max(f[i - 1], f[i]); 39 if (def[i] >= mid) 40 continue; 41 int l = max(i - ::r, 1), r = min(i + ::r, n); 42 f[r] = max(f[l - 1] + mid - def[i], f[r]); 43 } 44 return f[n] <= k; 45 } 46 47 inline void solve() { 48 for (int i = 1; i <= n; i++) { 49 int l = max(i - ::r, 1), r = min(i + ::r, n); 50 def[i] = ps[r] - ps[l - 1]; 51 } 52 53 ll l = 0, r = 2e18; 54 while (l <= r) { 55 ll mid = (l + r) >> 1; 56 if (check(mid)) 57 l = mid + 1; 58 else 59 r = mid - 1; 60 } 61 printf(Auto, l - 1); 62 } 63 64 int main() { 65 init(); 66 solve(); 67 return 0; 68 }
Educational Codeforces Round 40 (Rated for Div. 2) Partial Solution
标签:条件 clu cer blank 影响 输入 证明 技术分享 tle
原文地址:https://www.cnblogs.com/yyf0309/p/9310653.html