标签：广播 maximum 功能 技术分享 比较 2.4 三层 span 特征
2.1 双层神经网络
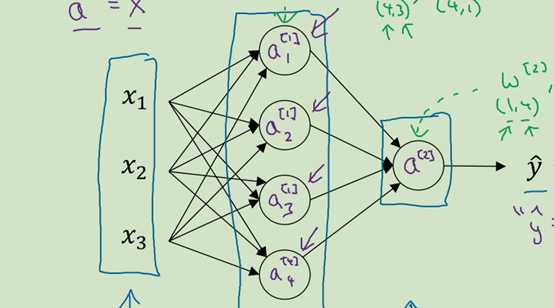
图 1
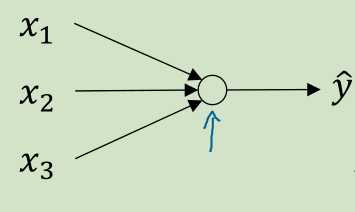
图 2
图1是一个双层网络模型，实际上有三层，但是通常把输入层给忽略掉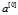 
称为输入层
注意
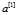层了，图1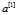
层有4个节点，图2只要1个，
所以图1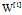 
应该是一个（4,3）的矩阵，图2的
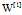是一个（1,3）的矩阵
ps：坚持将前一层的特征的权重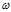
做成一列放入
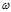矩阵中，所以每一个
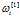都是（3,1）的列向量
以前一直都是使用，np.dot(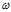
.T,X),这里也同样也沿用这个设定
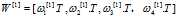所以
，所以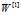
是一个（4,3）矩阵
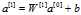，b是一个[4,1]的列向量，要生成矩阵节点在前
图1的正向传播算法：
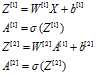
A,Z的横向表示第几个样本，竖向表示第几个节点
2.2理解m个样本向量化
重点在于np.dot这个函数，向量的点积运算
C=np.dot(A,B)
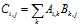
这是点积运算的定义（下面的W值得是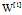
）
W是一个（4,3）的矩阵，表示总共有 4行3个特征权重 组成的权重矩阵
X是一个（3，m）的矩阵，表示有m个样本，每个样本有3个特征
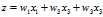观察z的计算形成，x的每一个特征与对应的权重相乘并累加
3个 x特征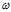 
权重相乘并累加成一个值，这个值就是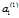
由于有4行这样的权重值，每一行的权重值都与第i个样本的3个特征相乘就形成了一个4为列向量如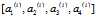
最终W与X点积，形成一个（4，m）的矩阵。至于+b就是numpy的广播功能了
注意b是一个(4,1)的列向量，每一个节点都有对应的b值 即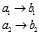
2.3 更多的激活函数
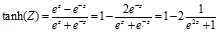
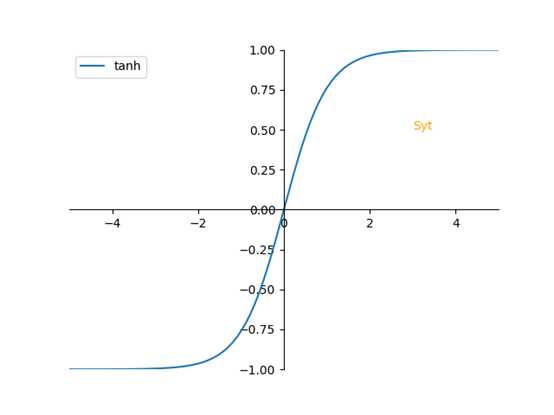
优点：平均值接近0，比起sigmod接近0.5的平均值，接近0，更易于下一层的计算
tanh各方面吊打sigmod，除了作为二分分类输出层时，才会使用sigmod作为作为激活函数
缺点：两个函数，都在Z很大的时候，梯度都接近0，这样会拖慢学习速率。梯度下降与学习率
以及梯度有关。
另外一个激活函数：relu函数 np.maximum(0,z), 比较0，和Z和大小，取大的
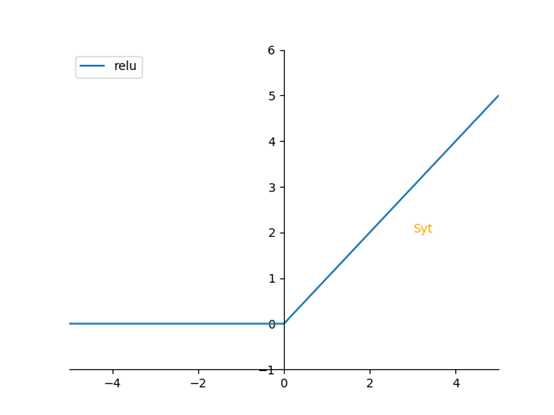特点：
1. 在Z>0时，梯度永远为1，
2. 在Z=0时，梯度为0，不过，你可以设置当Z=0时，梯度为多少
3. 缺点：当Z为负数时，顺带的也把梯度变成0了，不好使用梯度下降的方法
这个激活函数很强大，就是这么强，当不知道选用什么激活函数时，就选这个reluc函数（修正线性函数）
带泄露的relu函数 ：np.maximum(0.01Z,Z)，他会在负值有一个平缓的线条，让其也有梯度
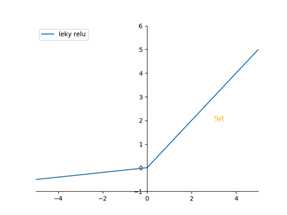为了表示清楚，选用的是0.1。 0.01是经验总结出来的一个参数
建立神经网络有一系列东西需要选择，如隐藏单元个数，激活函数，初始化
这些东西全靠经验选择出的，选择困难户
2.4 非线性激活函数的必要性
如果去掉非线性激活函数，那么你的输出与输入还是一个成线性关系，那么你后面的无论有多少隐藏层，都会等价于只做了一个线性输出。
在输出层会有可能需要做线性变换，才会用到线性激活函数。
中间隐藏层，如果需要做一些伸缩变化，也会用到线性激活函数（这种情况很复杂）
2.5 激活函数的导数
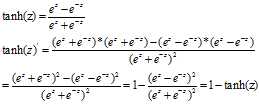
注释：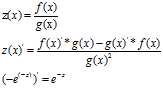
记住：a=tanh(z) a‘=1-a2
Relu函数以及带泄露的Relu函数：记住在z=0处是没有导数的，因为左右的偏导不相等，需要自己定义
2.6 神经网络下的梯度下降
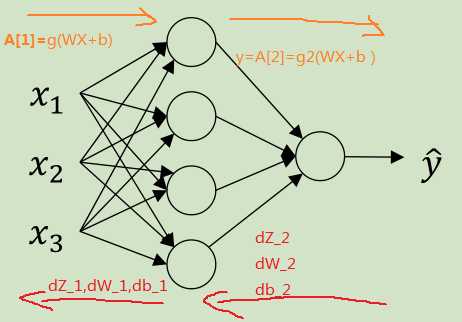
正反向传播公式计算
正向请翻上面
假设这是一个二分分类的双层神经网络
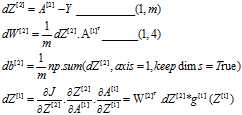
注意点：
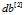是一个列向量，在横向累加，所以axis=1，为了确保累加之后不会出现一个秩为1的数组，所以调用keepdims=True
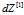时，
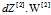与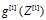
是对应为相乘，不再是点积了
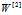是一个(1,4)转置之后是一个（4,1），
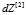是一个（1，m），点积之后变成（4，m）
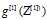是一个(4,m)矩阵，对应位相乘。这是从矩阵形状来看
dZ_1的计算并不需要累加，且不需要累加到m，然后除以m
还剩下一个随机初始化权重，留到明天学习
标签：广播 maximum 功能 技术分享 比较 2.4 三层 span 特征
原文地址：https://www.cnblogs.com/sytt3/p/9311275.html
