标签:技术分享 span 处理 子列 检查 描述 移动 步骤 分享图片
最大子列和问题的四种处理方法
(着重理解“分而治之”的思想)
问题描述:
什么是最大子列和问题?
假设给定一个数组: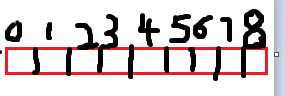
其目标在求这个数组中对于任意存在的连续子列,子列和最大的值。当最大子列和大于0时,即为该值。当最大的子列和的值小于0时,返回0值。
为了方便讨论,假设该数据是int 型数组,对于其它类型的数组,方法是一样的。
方法一:直接利用循环进行遍历—简单粗暴

方法二:简单粗暴法的优化
每一个子列,通过 i 确定子列的上界,通过 j 确定子列的下界。下界 j 是一点一点向后移动,每次移动一位。加入有两个子列A和B,它们具有共同的上界,且下界A-j = B-j +1
则SubtotalA = SubtotalB +1 依据此关系的存在,我们只需要二重循环即可解决问题。不再需要K循环。

方法三:分而治之—递归方法
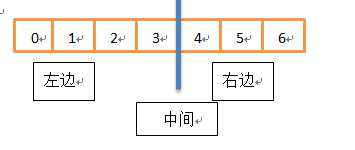
主要思想:最大子列和的存在只有三种可能:左边数组、右边数组、横跨左右数组;根据最大子列和的这种特性,求一个数组的最大子列和可以分为下面的步骤:
1、将数组分为左右两个部分
2、求左边数组的最大子列和 // 这是一个递归的过程,因为左边右边数组的最大子列和的求法依然采用步骤
3、求右边数组的最大子列和 // 这是一个数组分割的过程,当被分割的数组只存在一个元素的时候,递归结束。
4、求横跨左右数组的最大子列和
5、比较得出整个数组的最大子列和


总结:递归的方法比较抽象,必须首先在逻辑上理清算法的步骤是什么,然后按照每一步骤去一步一步实现代码,其中递归的实现不必去追究这个递归具体是怎样操作的。
方法四:在线处理—即顺序扫描数组,扫描即处理
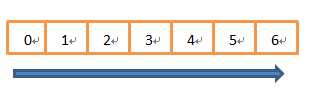
这种算法的思想是:只有当前面序列的和大于0时,它对后面的的序列才会变得有用,当前面的序列和都已经小于零,加上前面的序列和一定会使后面的序列和变下。
所以就一直检查序列和是否小于0,当小于0的时候将其抛弃。

标签:技术分享 span 处理 子列 检查 描述 移动 步骤 分享图片
原文地址:https://www.cnblogs.com/ziwangahu/p/9314382.html