标签:org blog logs strong lin vijos image log get
由于没有固定的源点和汇点,也不存在什么最大/小流之说了。存在可行流的条件是所有点均满足流量平衡性质。流量平衡指的是,对于每个点入流量=出流量。
如果每条边只有上界,没有下界,那只要让每条边的流量均为0,一定存在满足条件的流,如果有些边有下界,那就不一定存在满足条件的流了。
首先我们假设每条边流量均为它的下界。那么此时问题就转化为了一个只有上界的网络流问题(即普通网络流问题)。但是这么做有一个问题:下界不满足流量平衡。
我们考虑利用剩余的流量去调整以满足流量平衡。具体来说,如果某个点x的入流大于出流,我们建立一个超级源S‘,建立一条$S‘\rightarrow x$相应容量的边;反之,如果某个点y的入流小于出流,我们建立一个超级汇T‘,建立一条$y\rightarrow T‘$相应容量的边。
例如:
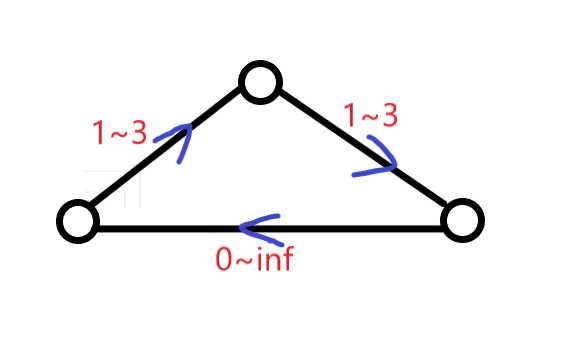
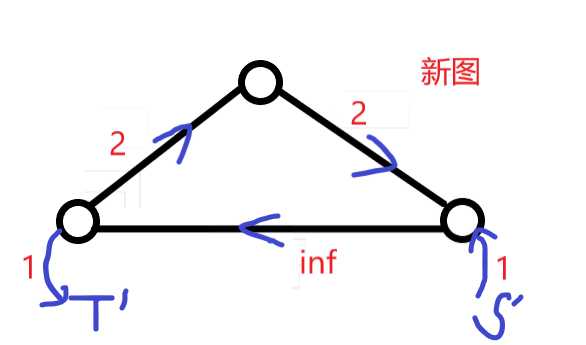
此时我们在新图上跑$S‘\rightarrow T‘$的最大流。由于最大流保证了除源点汇点外其余点均满足流量平衡,故新图中除了S‘,T‘其余点均满足流量平衡,那么去掉S‘和T‘所连的边,再加上原先的下界流量,如果满流则说明满足流量平衡,原图必然存在可行流;否则不存在。
考虑将其转化为无源汇的问题。
将T向S连一条容量上界为inf,下界为0的边,那么如果$T\rightarrow S$这条边有流量流过,说明原图是存在可行流的。
首先按照上述方法判断出无解情况。
针对有解情况,显然当前方案是可行的,但不一定最优。我们将上面所述的新图删去S‘,T‘以及它们所连的边,形成一个流量不平衡的图(但是这没关系,因为它和原图合并后是满足流量平衡的)。我们在这张图中继续增广(增广的过程保证是平衡的),即再跑一遍最大流,得到的就是答案。
注意:第二遍的答案就是最终的答案,不用加上第一遍最大流的答案,因为第一遍搜索出来的边T到S的流量可能是存在的,而第二遍搜索的时候会把这些流弹回去(反向边的存在),已经包含第一遍的流值了。
由于流量有下界,因此是存在非零最小流的。
同样按照上述方法判断出无解情况。
注意由于要求流量最小,按照最大流那样直接增广是不行的。(感性理解:直接跑求的是最大流,而我要求最小流,显然文不对题。)
例如:
增广后的流为200,但是原图中的最小流为100,这是因为我们没有运用循环流,也就是$2\rightarrow 1$这条边。由于我们求的是最小流,所以事实上我们想尽可能多走一些边。
我们先不加从T到S的边,直接增广,如下图:
然后再加那条边(注意原先边的流量还是要保存着的),再增广一次,此时边(T,S)的剩余流量就是原图的最小流。(感性理解:先跑一次最大流把流量尽可能跑完,剩下的流量就是最小流。)
标签:org blog logs strong lin vijos image log get
原文地址:https://www.cnblogs.com/bestFy/p/9310825.html