【模板】单源最短路径——Floyd

标签：技术   tle   原理   font   pre   动态规划   src   遍历   邻接矩阵   

抱歉这几天 晚上一直认真 （颓废）打模拟赛 一直没写博客  然后今天学了最短路  然后  马上过来码一下

以下内容  有的是搬得那些大佬们得博客  也谢谢他们

1.Floyd

感觉 Floyd 是比较常见的 最短路算法  而且也挺好用得

算法思想原理：

     Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

      从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

3).Floyd算法过程矩阵的计算----十字交叉法

方法：两条线，从左上角开始计算一直到右下角 如下所示

给出矩阵，其中矩阵A是邻接矩阵，而矩阵Path记录u,v两点之间最短路径所必须经过的点

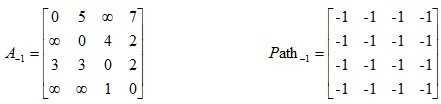
相应计算方法如下：

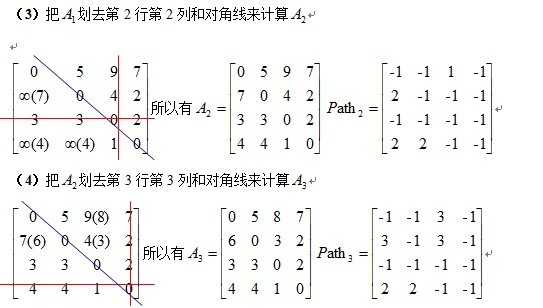
最后A₃即为所求结果

看一下代码：

//直接上核心部分吧

for(int k=1;k<=n;k++)//中间点
    for(int i=1;i<=n;i++)//
  i,j 表示 i -> j点
        for(int j=1;j<=n;j++)
            g[i][j]=min(g[i][j],g[i][k]+g[k][j]);

【模板】单源最短路径——Floyd

标签：技术   tle   原理   font   pre   动态规划   src   遍历   邻接矩阵   

原文地址：https://www.cnblogs.com/_Kurisu/p/9337658.html