标签:ext display play rac main XML 上线 include data
随着新版百度空间的上线,Blog宠物绿豆蛙完成了它的使命,去寻找它新的归宿。
给出一个有向无环图,起点为1终点为N,每条边都有一个长度,并且从起点出发能够到达所有的点,所有的点也都能够到达终点。绿豆蛙从起点出发,走向终点。
到达每一个顶点时,如果有K条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走向每条路的概率为 1/K 。
现在绿豆蛙想知道,从起点走到终点的所经过的路径总长度期望是多少?
这很明显是一道数学期望的题目。
拿样例来说
点1一开始肯定是有1.00的几率到达的,它有两条出边,分别到达点2和点3,那么,点2和点3就各有0.50的几率到达。 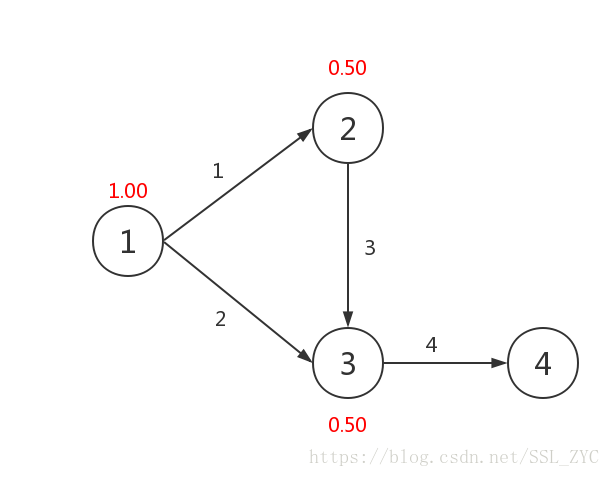
那么,点2又有一条出边到达点3,那么点3到达的几率就在原来的基础上又加上了点2的到达几率,所以点3的到达几率为1.00。 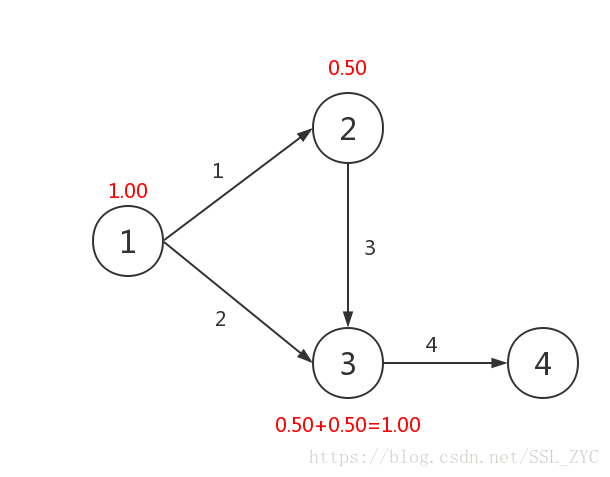
然后点3就只有一条出边,通向点4,所以点4到达几率就为1.00。
每次当我们访问到一个点时,就讲答案sum加上它到达的概率×边权,即
且这个点的期望也要加上s[x]÷num[x]
然后继续向下搜索,搜到点n时就返回,然后将期望值减去s[x]÷num[x],防止重复计算。
#include <cstdio> #include <iostream> using namespace std; int n,m,x,y,t; double z,sum,s[300011],num[300011],head[300011],k; struct edge //邻接表 { int to,next; double dis; }e[500011]; void add(int from,int to,double d) //建边 { t++; e[t].dis=d; e[t].to=to; e[t].next=head[from]; head[from]=t; } void dfs(int x) { if (x==n) return; //到达终点 for (int i=head[x];i;i=e[i].next) { int v=e[i].to; double l=s[x]/num[x]; //计算路径长度期望 s[v]+=l; //加上期望 sum+=e[i].dis*l; //答案 dfs(v); s[v]-=l; //减掉期望 } } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { scanf("%d%d%lf",&x,&y,&z); add(x,y,z); //建边 num[x]++; } s[1]=1.00; dfs(1); printf("%0.2lf\n",sum); return 0; }
标签:ext display play rac main XML 上线 include data
原文地址:https://www.cnblogs.com/hello-tomorrow/p/9340789.html