标签:因此 .com step 技术 bubuko 直线 图片 com line
多项式函数是长这样的函数:
\[f(x)=a_0+a_1x+a_2x^2+\ldots+a_nx^n\]
它有一个很\(Nice\)的特点:代人\(x\),在\(O(n)\)的时间内就可以求出\(f(x)\),没有任何障碍.
但是这样的函数:
\[g(x)=e^x\]
\[h(x)=sin x\]
想得到\(g(3)\)或是\(h(7)\)就比较困难了。因此我们需要用多项式函数去"取代"这些奇怪的函数。
step1:用\(y=a_0+a_1x\)去逼近它.
具体的方法是让它的斜率等于\(f(x)\)在\(x=0\)时的导数:1
让直线过\((0,1)\),于是得到的直线\(y=x+1\)
效果如下图:
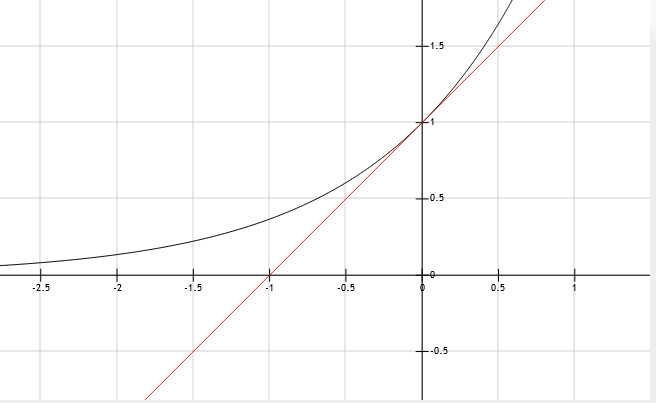
在\(x\)离\(0\)很近的时候还是比较精确的.
step2:用\(g(x)=a_0+a_1x+a_2x^2\)这个二次多项式去逼近它.
具体方法是让它在\(x=0\)处的函数值、导数值、二阶导数值与\(f(x)\)相等.
\[f(x)=e^x,f(0)=1\]
\[f'(x)=e^x,f'(0)=1\]
\[f''(x)=e^x,f''(0)=1\]
再看这个二次多项式:
\[g(x)=a_0+a_1x+a_2x^2,g(0)=a_0\]
\[g'(x)=a_1+2a_2x,g'(0)=a_1\]
\[g''(x)=2a_2,g''(0)=2a_2\]
因为要让\(f(x),f'(x),f''(x)\)与\(g(x),g'(x),g''(x)\)分别对应相等,所以:
\[a_0=1,a_1=1,2a_2=1\]
所以\(g(x)=1+x+\frac{x^2}{2}\)
效果如下图.
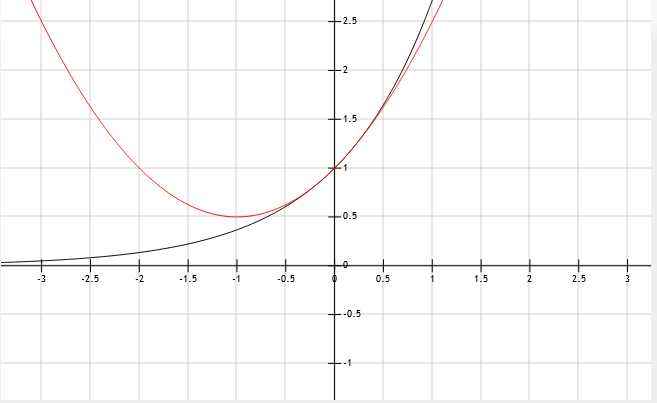
已经非常接近了呢.
step3:用\(g(x)=a_0+a_1x+a_2x^2\)这个二次多项式去逼近它.
标签:因此 .com step 技术 bubuko 直线 图片 com line
原文地址:https://www.cnblogs.com/cute-hzy/p/9343739.html