标签:center cti lap isequal end lock break 基本 数学
作者:桂。
时间:2018-07-21 08:42:18
链接:https://www.cnblogs.com/mia1004/p/9345533.html
前言
主要记录系统结构模型的分析思路,例如对于一个复杂的控制系统,不同模块之间存在一定的连接关系,但模块数量多大则难以理清楚头绪,更抓不清主要矛盾、次要矛盾,因此需要借助数学手段辅助解决。 该模型在分析设备的控制系统同样有效。
一、原理简介
对于系统各个模块的连接关系:
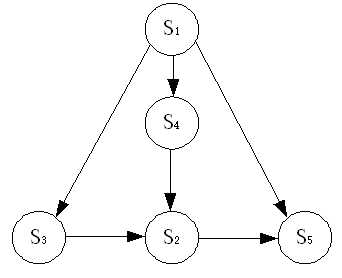
A-邻接矩阵(adjacency matrix)
在介绍拉普拉斯矩阵的时候,有提到过邻接矩阵的概念,其意义为有向图的连接状态,为bool型数据。
此处的邻接矩阵为:
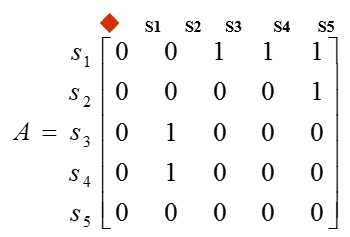
邻接矩阵体现的是当下的连接状态,但S1虽没有直达S2的车次,S1-S4-S2/S1-S3-S2,转车可达。因此我们希望有这样一个矩阵:给定始发站、终点站,无论转车与否,是否可达?这样的矩阵我们成为:可达矩阵。
B-可达矩阵(reachability matrix)
邻接矩阵记作A,可达矩阵记作R,首先分析$A^k$,其中k为矩阵的幂指数。容易理解:$A^k$表征了Si 经过k步 -> Sj的可达性。
而可达矩阵呢?无论走1步到达、2步到达、...、N步到达,都可以表示二者可达。因此可达矩阵的表达式为:
$R = A^0 + A^1 + A^2 + ... + A^N$
对应就是级数展开式:
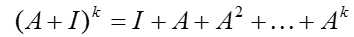
实际应用中如何求解呢?可以通过基本判据:
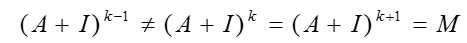
M就是可达矩阵R。
C-ISM分析(ISM: interpretive structural modeling)
ISM在可达矩阵R的基础上进行层次划分,仅介绍如何应用。首先介绍3个基本概念:
1)可达集合Rs;可达矩阵中要素Si对应的行中,包含有1的矩阵元素所对应的列要素的集合
2)先行集合Qs;可达矩阵中要素Si对应的列中,包含有1的矩阵元素所对应的行要素的集合
3)交集RQs。1)2)的交集。
下面介绍层次分析步骤:
1)掐头去尾
根据Rsi 相交 RQsi = Rsi确定顶层结构
根据Qsi 相交RQsi = Qsi确定底层结构
2)确定中间结构
抽出顶层之后,重新生成可达矩阵以及对应的三个集合,重新确定顶点,重叠反复。
二、示例分析
以邻接矩阵举例:
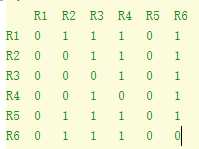
这里情况较为特殊,掐头去尾之后,已经没有中间元素,不再赘述。对应代码:
clc;clear all;close all;
%{
R1 R2 R3 R4 R5 R6
R1 0 1 1 1 0 1
R2 0 0 1 1 0 1
R3 0 0 0 1 0 1
R4 0 0 1 0 0 1
R5 0 1 1 1 0 1
R6 0 1 1 1 0 0
%}
%% 邻接矩阵
A = [0 1 1 1 0 1
0 0 1 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
0 1 1 1 0 1
0 1 1 1 0 0];
%% 计算可达矩阵
[ReachMatrix, k] = reach_matrix(A);
%% 对可达矩阵进行分解
%可达集合 => Ri对应的行中,包含1的元素所对应列要素的集合
Rsi = {};
N = size(ReachMatrix,1);
for i = 1:N
Rsi{i} = find(ReachMatrix(i,:)==1);
end
%先行集合 => Ri对应的列种,包含1的元素所对应行要素的集合
Qsi = {};
for i = 1:N
Qsi{i} = find(ReachMatrix(:,i)==1);
end
%交集,可达集合与先行集合的交集
RQsi = {};
for i = 1:N
RQsi{i} = intersect(Rsi{i},Qsi{i});
end
%% 层级分解
% for i = 1:N
% Rsi{i}
% Qsi{i}
% pause()
% end
%这里找出顶点、底层之后,所有点都用完了,因此较简便
%找顶层+找底层
for i = 1:N
if isequal(Rsi{i},RQsi{i}‘)
disp(‘顶层: ‘)
Rsi{i}
end
if isequal(Qsi{i},RQsi{i})
disp(‘底层: ‘)
Qsi{i}
end
end
可达矩阵求解:
function [R, k] = reach_matrix(A)
I = eye(size(A));
R = A+I;
k = 0;
while 1
Rnew = R*(A+I)>0;
if isequal(R,Rnew);
k=k+1
break;
end
R = Rnew;
k = k+1;
end
最终层次结果:
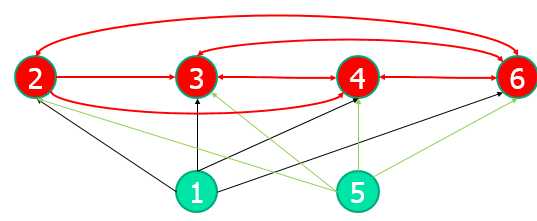
该方法在分析复杂系统,真是一个很棒的工具。
标签:center cti lap isequal end lock break 基本 数学
原文地址:https://www.cnblogs.com/mia1004/p/9345533.html