标签:mon sub nbsp 计算 tps learn 假设 mil 概念
之所以起这个名字是因为对应之前的搭配推荐模型,如之前的博客 基于图像信息的搭配商品推荐 中所述,可以看做是基于单因素对搭配进行建模,即认为搭配的商品应该在单因素--风格上相似,然后在对商品映射后的latent space即风格空间中,搭配的商品的距离会更接近。
然后更进一步很自然的想法就是:
1)相互搭配的商品是可以在多个因素上近似的,比如款式、材质、印花、颜色等,而用风格这一个概念来概括就显得有些粗糙。
2)可以与一个主商品进行搭配的pair商品也可以是多种风格的,比如一件T恤可以跟不同风格的下装搭配,搭出运动、休闲、淑女等不同的风格。
基于这两种不同的思路,可以采用不同的两种方式进行建模。
这篇paper提出一种方法:Mixtures of Non-Metric Embeddings for Recommendation, 简称Monomer,是为了对multiple localized notions of relatedness进行建模,即搭配的商品pair之间是可以有多种方面的因素的,而之前的搭配建模方式是只能学习到global notion of relatedness,这也是这种方法能够产出多样性搭配推荐结果的关键点。
建模方式:
1)Low-rank Mahalanobis Metric
将E看作是商品原始向量到latent space向量的映射关系,则映射后商品pair之间的距离是
![]()
2)Multiple, Non-Metric Embeddings
因为考虑到相互搭配的商品是可以在多个因素上近似的,比如款式、材质、印花、颜色等,而用风格这一个概念来概括就显得有些粗糙。所以可以有多个E,即用Ek来表示,每个Ek可以看作是一种特征提取的方式。其中第k种映射空间上,商品pair之间的距离为:
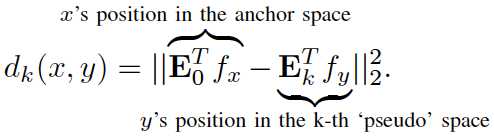
3)Probabilistic Mixtures of Embeddings
将N种映射方式上的预测距离加权求和,那么权重如何确定呢?考虑到非对称的设定,应该主要与主商品的特征相关。如下:
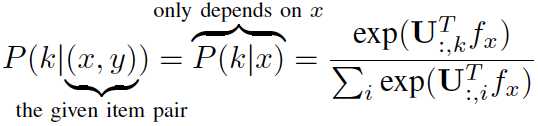
where U is a newly-introduced F*N parameter matrix with U:;k being its k -th column.
最终,商品pair的距离为:
![]()
模型训练:
采用最大似然估计的方式计算loss并进行模型训练。
![]()
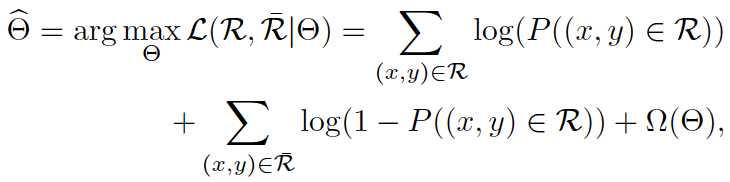
这篇paper同样是基于多因素进行搭配关系的建模,但与上一篇paper不同的是,主要假设是:可以与一个主商品进行搭配的pair商品可以是多种风格的。
paper提出了一种end-to-end的模型,将每个item映射到latent space上的K+1的向量,其中1个向量代表该item,另外K个向量代表该item的K个compatible prototypes,这些prototypes反应了搭配建模中的多样性,即可以与一个主商品进行搭配的pair商品可以是多种风格的。这K+1个向量即是该item的 compatibility family。
建模方式:
1)Projected Compatibility Distance
PCD是用于衡量两个商品之间的搭配关系的。
每个item可以被E0映射为一个向量;另外还可以被Ek(k=1,2,...,K)映射为K个向量,每个向量都靠近与其搭配的商品所组成的cluster。PCD的计算方式如下:
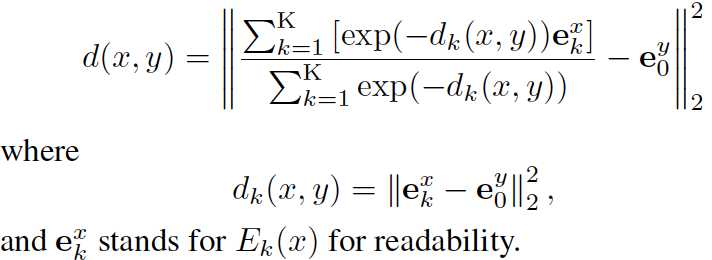
用图来表示的话:
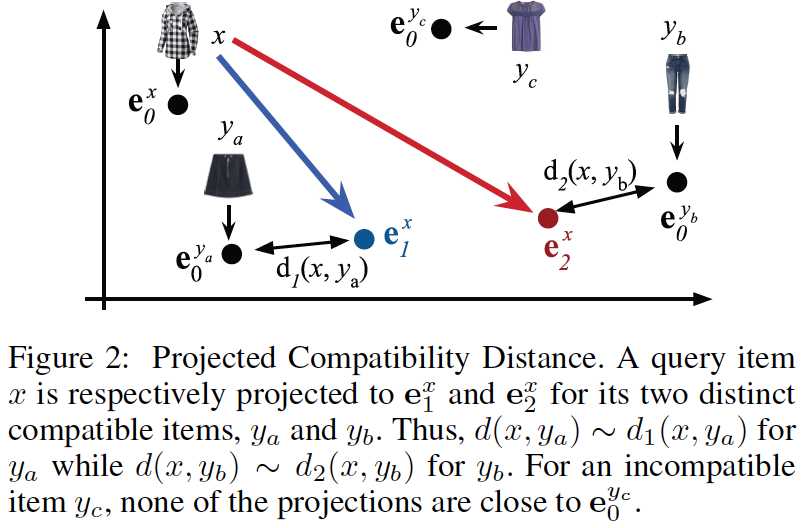
2)最大似然估计
Ek(k=1,2,...,K)的大多数网络层参数都是共享的,只有最后一层参数是独立训练的。
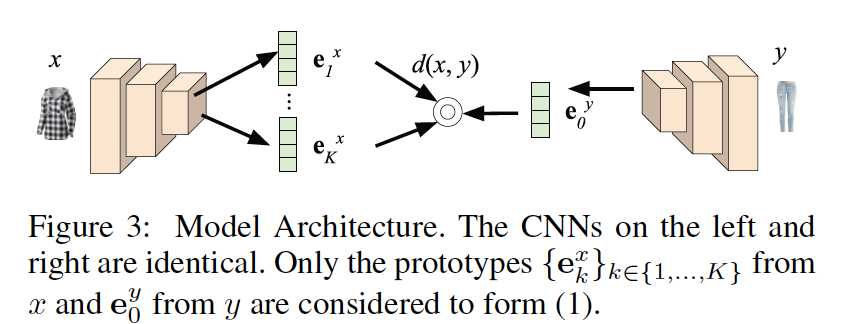
使用最大似然估计进行建模:
![]()
模型训练:
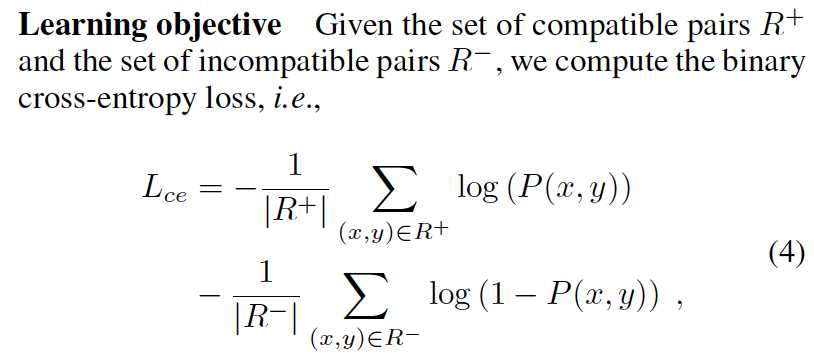
标签:mon sub nbsp 计算 tps learn 假设 mil 概念
原文地址:https://www.cnblogs.com/bentuwuying/p/9348458.html