标签：获得 场景 矩阵 bsp 关系 alt 集合 img 联系
什么是仿射变换？
原理：1、一个任意的仿射变换都能表示为 乘以一个矩阵（线性变换） 接着再 加上一个向量（平移）
2、综上所述，我们能够用仿射变换来表示：
1）旋转（线性变换）
2）平移（向量加）
3）缩放操作（线性变换）
事实上，仿射变换代表的是两幅图之间的关系。
3、我们通常使用2*3矩阵来表示仿射变换：
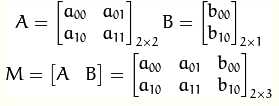
考虑到我们要使用矩阵A和B对二维向量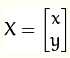
做变换，所以也能表示为下列形式：
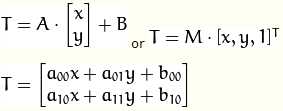
怎样才能求得一个仿射变换？
1、我们在上文有提到过仿射变换基本表示的就是两幅图片之间的联系。关于这种联系的信息大致可以从一下两种场景获得：
1）我们一直 X 和 T 而且我们知道他们是有联系的，接下来我们的工作就是求出矩阵 M
2）我们已知 M 和 X，想要球的 T。我们只要应用算式 T = M*X 即可，对于这种联系的信息可以用矩阵 M 清晰的表达或者可以用两幅图片之间的集合关系来表达
2、因为矩阵 M 联系着两幅图片，我们以其表示两图种各三点直接的联系为例。见下图：
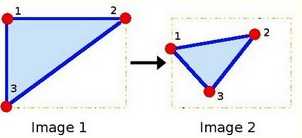
3、点1，2，3（在上图1中形成一个三角形）与图二中的三点一一映射，仍然形成三角形。
标签：获得 场景 矩阵 bsp 关系 alt 集合 img 联系
原文地址：https://www.cnblogs.com/zhibei/p/9349006.html
