标签:一点 sig 参数 idt 宽度 存在 部分 ros 导致
只要模型是一层一层的,并使用AD/BP算法,就能称作 BP神经网络。RBF 神经网络是其中一个特例。
一、什么是径向基函数
1985年,Powell提出了多变量插值的径向基函数(RBF)方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
二、RBF神经网络
RBF神将网络是一种三层神经网络,其包括输入层、隐层、输出层。从输入空间到隐层空间的变换是非线性的,而从隐层空间到输出层空间变换是线性的。流图如下:
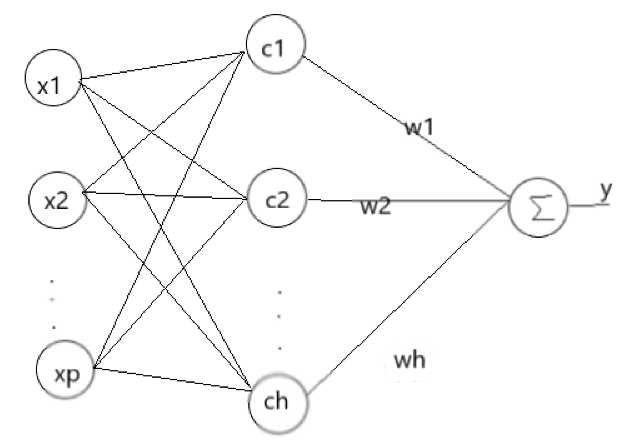
RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和,此处的权即为网络可调参数。其中,隐含层的作用是把向量从低维度的p映射到高维度的h,这样低维度线性不可分的情况到高维度就可以变得线性可分了,主要就是核函数的思想。这样,网络由输入到输出的映射是非线性的,而网络输出对可调参数而言却又是线性的。网络的权就可由线性方程组直接解出,从而大大加快学习速度并避免局部极小问题。
径向基神经网络的激活函数可表示为:
![]()
其中xp为第p个输入样本,ci为第i个中心点,h为隐含层的结点数。径向基神经网络的结构可得到网络的输出为:
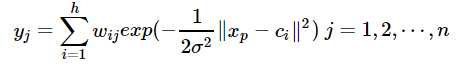
当然,采用最小二乘的损失函数表示:
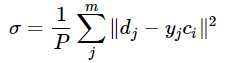
三、RBF神经网络的学习问题
求解的参数有3个:基函数的中心、方差以及隐含层到输出层的权值。
(1)自组织选取中心学习方法:
第一步:无监督学习过程,求解隐含层基函数的中心与方差
第二步:有监督学习过程,求解隐含层到输出层之间的权值
首先,选取h个中心做k-means聚类,对于高斯核函数的径向基,方差由公式求解:
![]()
cmax为所选取中心点之间的最大距离。
隐含层至输出层之间的神经元的连接权值可以用最小二乘法直接计算得到,即对损失函数求解关于w的偏导数,使其等于0,可以化简得到计算公式为:
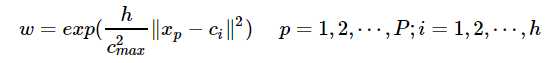
(2)直接计算法
隐含层神经元的中心是随机地在输入样本中选取,且中心固定。一旦中心固定下来,隐含层神经元的输出便是已知的,这样的神经网络的连接权就可以通过求解线性方程组来确定。适用于样本数据的分布具有明显代表性。
(3)有监督学习算法
通过训练样本集来获得满足监督要求的网络中心和其他权重参数,经历一个误差修正学习的过程,与BP网络的学习原理一样,同样采用梯度下降法。因此RBF同样可以被当作BP神经网络的一种。
四、RBF神经网络与BP神经网络之间的区别
1、局部逼近与全局逼近:
BP神经网络的隐节点采用输入模式与权向量的内积作为激活函数的自变量,而激活函数采用Sigmoid函数。各调参数对BP网络的输出具有同等地位的影响,因此BP神经网络是对非线性映射的全局逼近。
RBF神经网络的隐节点采用输入模式与中心向量的距离(如欧式距离)作为函数的自变量,并使用径向基函数(如Gaussian函数)作为激活函数。神经元的输入离径向基函数中心越远,神经元的激活程度就越低(高斯函数)。RBF网络的输出与部分调参数有关,譬如,一个wij值只影响一个yi的输出(参考上面第二章网络输出),RBF神经网络因此具有“局部映射”特性。
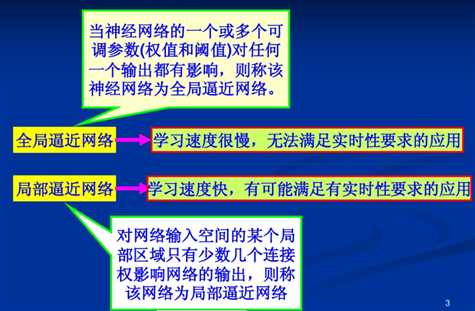
所谓局部逼近是指目标函数的逼近仅仅根据查询点附近的数据。而事实上,对于径向基网络,通常使用的是高斯径向基函数,函数图象是两边衰减且径向对称的,当选取的中心与查询点(即输入数据)很接近的时候才对输入有真正的映射作用,若中心与查询点很远的时候,欧式距离太大的情况下,输出的结果趋于0,所以真正起作用的点还是与查询点很近的点,所以是局部逼近;而BP网络对目标函数的逼近跟所有数据都相关,而不仅仅来自查询点附近的数据。

对于BP神经网络:
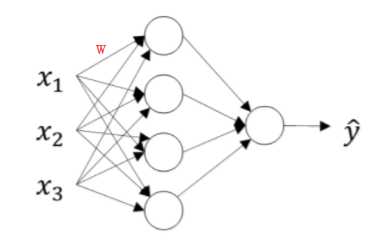
如上,要求w的话,每个yi都和w有关系,这个是计算量增加的一个重要原因。
标签:一点 sig 参数 idt 宽度 存在 部分 ros 导致
原文地址:https://www.cnblogs.com/pinking/p/9349695.html