标签:注意 return 两种 main 若是 技术 book 存储 顶点
原创
图的遍历有DFS和BFS两种,现选用DFS遍历图。
存储图用邻接矩阵,图有v个顶点,e条边,邻接矩阵就是一个VxV的矩阵;
若顶点1和顶点5之间有连线,则矩阵元素[1,5]置1,若是无向图[5,1]也
置1,两顶点之间无连线则置无穷,顶点到顶点本身置0。
例如:
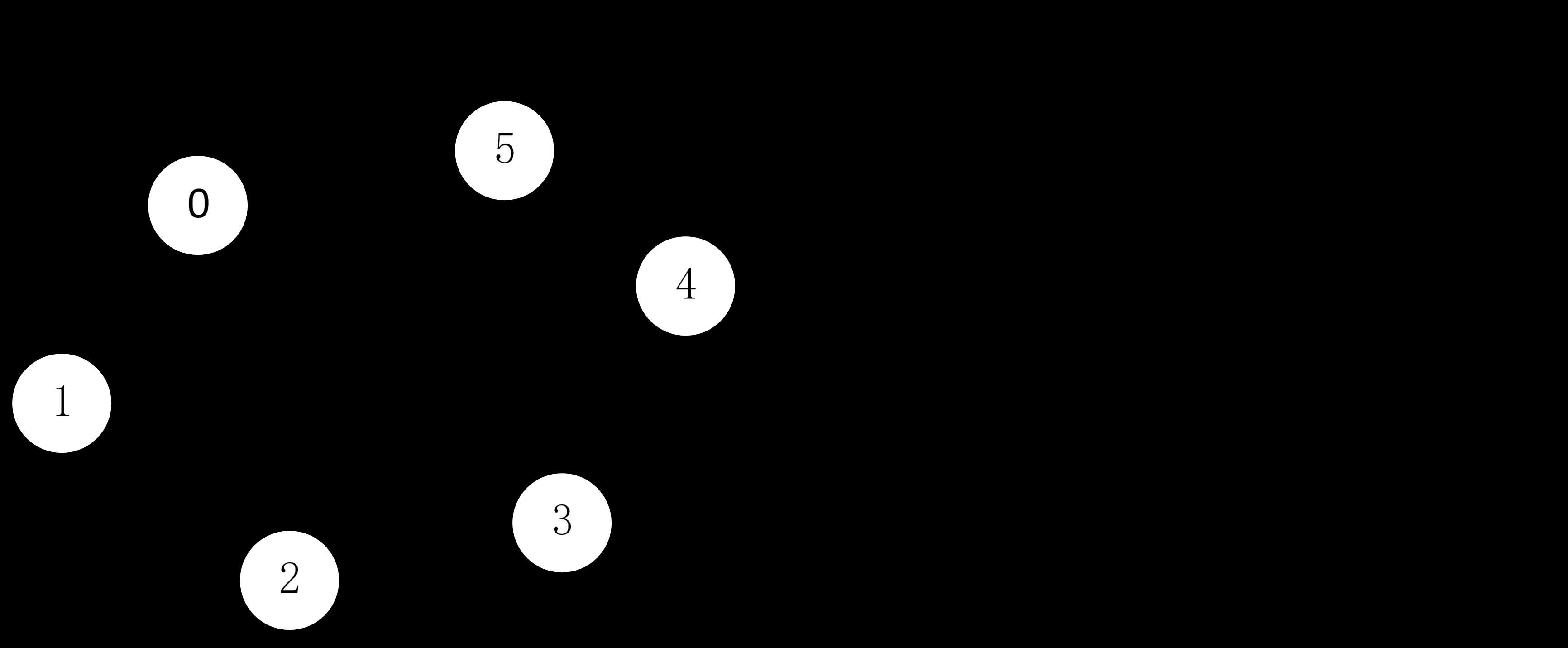
邻接矩阵为:

遍历思路:
随便选择一未访问过的顶点v1作为遍历起点,访问v1,再选择与v1连接的点v2作为起始点,访问v2;
再选择与v2连接的点作为起始点v3,访问v3,假设v3是孤立点,则v3不能往下访问,回溯到v2,再以v2
作为起点,访问与v2连接的其他未被访问过的顶点,假设是v4,则再以v4为顶点,访问v4,再选择与v4
连接的顶点为起始点......直到全部顶点都被访问过一遍。
在上图中,假设以顶点2为起点进行图的遍历,则先访问顶点2,再访问顶点1,注意,并不是先访问
3,因为在扫描邻接矩阵时,在每行是从左向右扫描的;再访问顶点0,再深搜下去访问顶点4,访问顶点
5,一直回溯,回溯到顶点2,再访问顶点3;访问顺序为:2 1 0 4 5 3
Java:
import java.util.*; public class 图的遍历_dfs { static int v; //顶点数 static int e; //边数 static int arr[][]; static int book[]; //标识顶点是否访问 static int max=99999; //无穷 static int total=0; //统计已访问顶点个数 static void graph_dfs(int ver) { //ver表示顶点 total++; book[ver]=1; //标记顶点ver已经访问过 System.out.print(ver+" "); if(total==v) { return; } for(int i=0;i<v;i++) { if(arr[ver][i]==1 && book[i]==0) { graph_dfs(i); } } return; } public static void main(String[] args) { Scanner reader=new Scanner(System.in); v=reader.nextInt(); e=reader.nextInt(); arr=new int[v][v]; book=new int[v]; //邻接矩阵初始化 for(int i=0;i<v;i++) { book[i]=0; for(int j=0;j<v;j++) { if(i==j) { arr[i][j]=0; } else { arr[i][j]=max; } } } //读入边 for(int i=0;i<e;i++) { int first_E=reader.nextInt(); int second_E=reader.nextInt(); arr[first_E][second_E]=1; arr[second_E][first_E]=1; } graph_dfs(0); //从顶点0开始遍历 } }
18:08:52
2018-07-22
标签:注意 return 两种 main 若是 技术 book 存储 顶点
原文地址:https://www.cnblogs.com/chiweiming/p/9350880.html