标签：height aaa 质数 alt 字符串hash alc 长度 namespace dash
Let‘s denote k k k -substring of s s s as a string subsk=sksk+1..sn+1−k subs_{k}=s_{k}s_{k+1}..s_{n+1-k} subsk?=sk?sk+1?..sn+1−k? . Obviously, subs1=s subs_{1}=s subs1?=s , and there are exactly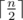 
such substrings.
Let‘s call some string t t t an odd proper suprefix of a string T T T iff the following conditions are met:
For evey k k k -substring (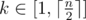
) of s s s you have to calculate the maximum length of its odd proper suprefix.
The first line contains one integer n n n (2<=n<=106) (2<=n<=10^{6}) (2<=n<=106) — the length s s s .
The second line contains the string s s s consisting of n n n lowercase Latin letters.
输出格式：Print 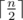integers. i i i -th of them should be equal to maximum length of an odd proper suprefix of i i i -substring of s s s (or −1 -1 −1 , if there is no such string that is an odd proper suprefix of i i i -substring).
15
bcabcabcabcabca
9 7 5 3 1 -1 -1 -1
24
abaaabaaaabaaabaaaabaaab
15 13 11 9 7 5 3 1 1 -1 -1 1
19
cabcabbcabcabbcabca
5 3 1 -1 -1 1 1 -1 -1 -1
The answer for first sample test is folowing:
Solution：
集训第二天，昨天HRZ学长讲的NOI2016我只搞出了一道（话说我是真的菜）。
今天的字符串专题讲了下本题，然后思路非常巧妙：字符串hash+类似kmp的方法。
首先字符串hash就随便讲下，直接将每位当作$k$进制数取模就好了，一般$k=131$然后模数搞个质数，当然为了防止出错，可以搞多模数。
然后我们发现本题的一个性质，那就是$ans[1]-2\leq ans[2]$，这个很显然啊，那么我们移项后得到$ans[1]\leq ans[2]+2$。
不难想到我们可以从最中间的情况开始考虑，然后往前枚举，对于当前答案$ans[cnt]$，可以肯定的是$ans[cnt]\leq ans[cnt+1]+2$，所以每次答案最多增加一个$2$，若不行就回退，最多减少$n$个$2$（注意不能小于$-1$）。学长说这有点像KMP的算法复杂度证明，显然有一共最多增加$\frac{n}{2}$个$2$，最多减少$\frac{n}{2}$个$2$，所以复杂度是$O(n)$的，具体实现时，只需要取出该长度的两个字符串hash值，比较一下直到相等就好了。有点玄学，但是还是能理解吧。
代码：
1 #include<bits/stdc++.h> 2 #define il inline 3 #define ll long long 4 #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) 5 #define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--) 6 using namespace std; 7 const ll N=2000005,M=131,mod1=998244353,mod2=19260817; 8 ll f[N],p[N],sum[N],ans[N>>1],cnt; 9 int n; 10 char s[N]; 11 12 il void solve(){ 13 sum[0]=1; 14 For(i,1,n) f[i]=(f[i-1]*M+s[i])%mod1,sum[i]=(sum[i-1]*M)%mod1; 15 int l,r; 16 cnt=n+1>>1; 17 if(n&1)ans[cnt]=-1,l=r=n+1>>1; 18 else { 19 l=n>>1,r=l+1; 20 s[l]==s[r]?ans[cnt]=1:ans[cnt]=-1; 21 } 22 ll p,q; 23 while(cnt--){ 24 ans[cnt]=ans[cnt+1]+2; 25 if(!cnt)break; 26 l--,r++; 27 p=-1,q=1; 28 while(ans[cnt]!=-1){ 29 p=(f[l+ans[cnt]-1]-f[l-1]*sum[ans[cnt]]%mod1+mod1)%mod1; 30 q=(f[r]-f[r-ans[cnt]]*sum[ans[cnt]]%mod1+mod1)%mod1; 31 if(p==q) break; 32 ans[cnt]-=2; 33 } 34 } 35 For(i,1,(n+1)>>1) printf("%lld ",ans[i]); 36 } 37 38 39 int main(){ 40 scanf("%d%s",&n,s+1); 41 solve(); 42 return 0; 43 }
标签：height aaa 质数 alt 字符串hash alc 长度 namespace dash
原文地址：https://www.cnblogs.com/five20/p/9353217.html
