标签:等于 || 斐波那契 角度 png i++ 结果 col 衡量
程序中循环嵌套通常要求嵌套2层。如果嵌套超过2层,需要重新考虑编码方式。背后的一个考量维度就是时间复杂度(五个判断维度:正确性、可读性、健壮性、时间复杂度、空间复杂度)。
时间复杂度是算法效率的衡量方法,可以简单判定一个算法是否优秀。
公式:T(n)= O(f(n))
解释:
T(n):语句总的执行次数是问题规模n的某个函数,这个函数用T(n)表
示。
f(n):辅助函数,是T(n)的同数量级函数。n趋近于无穷大时,使
T(n)/f(n)的极限值出现不等于零的常数。
O:时间复杂度的表示。
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,需要分析T(n)随n的变化情况并确定T(n)的数量级。
最简单判断方法:找最坏情况。
举例:
1 for (int i = 0; i < n; i++) 2 { 3 for (int j = 0; j < n; j++) 4 { 5 a[i][j]=0; 6 for (int k = 0; k < n; k++) 7 { 8 c[i][j] = a[i][k] * b[i][k]; //最坏情况,执行n^3。时间复杂度表示为:T(n)=O(n^3) 9 10 } 11 } 12 }
常数阶
1 Console.WriteLine("1"); 2 -------------------------------- 3 int a=0; 4 Console.WriteLine(a);
只执行一次,时间复杂度O(1)
线性阶
1 int x = 100, sum = 0; 2 for (int i = 0; x < n; i++) 3 { 4 sum = sum + i; 5 }
问题规模:sum = sum + i 线性增长,每次增长1,时间复杂度O(n)。
平方阶
1 for (int i = 0; i < n; i++) 2 { 3 for (int j = 0; j < n; j++) 4 { 5 Console.WriteLine("abc"); 6 } 7 }
外层代码执行1次,内层执行N次,外层执行N次,总共执行N^2次,时间复杂度O(n^2)。
对数阶
1 int i = 1; n = 100; 2 while (i < n) 3 { 4 i = i * 2; 5 }
最坏方法判断:每次都为2的倍数,i>=n,循环结束。
则 2^x=n,求对数即可。x=log2n,循环时间复杂度O(log2n)
常数阶O(1),对数阶O( ),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n^2),立方阶O(n^3),k次方阶O(n^k),指数阶O(2^n)。
随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率逐渐降低。
实际应用:完成1+2+3+4………+100=5050的编码。
普通人:
1 for(int i=1;i<=100;i++) 2 { 3 sum=sum+i; 4 }
时间复杂度:O(n)
高斯的算法(首位相加方法):
1 Sum=(1+100)*100/2
时间复杂度:O(1)
首位相加方法只执行一次,普通方法执行n次,所以,这种方法效率高。
用代码简单判断程序执行时间:


斐波那契数列(递归部分)
1 static int Fibonaccil(int n) 2 { 3 if (n == 1 || n == 2) 4 { 5 return 1; 6 } 7 return Fibonaccil(n - 1) + Fibonaccil(n - 2); 8 }
时间复杂度:O(2^n)
递归求解F(n),必须先计算F(n-1)和F(n-2),计算F(n-1)和F(n-2),又必须先计算F(n-3)和F(n-4)。。。。。。以此类推,直至必须先计算F(1)和F(0),然后逆推得到F(n-1)和F(n-2)的结果。
可以从细胞分裂的角度考虑:
细胞分裂。1个细胞第一次分裂,2个细胞。第二次分裂,4个细胞。。。。。。。以此类推,N次分裂后,有2^n个细胞。
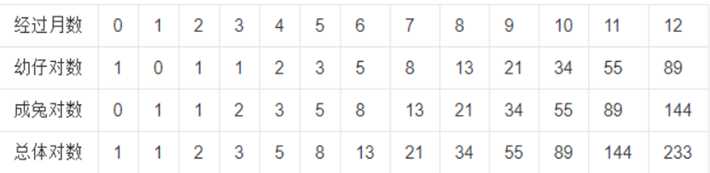
斐波那契数列解释:
斐波那契数列,又称为“兔子数列”。
起始状态:
1、一对兔子,每对兔子每个月能生出一对小兔子。
2、新兔子两个月后具有繁殖能力。
第一个月有1对兔子,第二个月后,小兔对数共有两对,第三个月有3对兔子,老兔子繁殖,新兔子没有繁殖能力。第4个月后有5对兔子。。。。。。。
标签:等于 || 斐波那契 角度 png i++ 结果 col 衡量
原文地址:https://www.cnblogs.com/sunice/p/9359332.html