标签:src bsp namespace queue sof one while continue soft
唯一分解定理:任何大于1的自然数都可以唯一分解成有限个质数的乘积
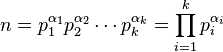
这里的 n > 1;
定理就是这样,我们来看一个题目: https://vjudge.net/problem/UVA-10892
首先我们可以将a、b进行分解 a = (p1^a1)*(p2^a2)......(pn^an),b = (p1^b1)*(p2^b2)......(pn^an)
它们的最小公倍数(LCM)我们也进行分解:r = (p1^r1)*(p2^r2) ...... (pn^rn)
这里就会有 ri = max{ai, bi} , 这样一来我们就可以构造所有的a和b的组合了,现在假设a的 pi项 的 ai 为 ri,则我们b的 pi项 对应的 bi 就可以取 [0, ri-1]共 ri 个值,同理对b的 pi项 的 bi 也可以取 ri,a就也有 ri 个可取的值,再加上a和b的 pi 项同时为 ri 这种情况,就一共有 2*ri+1 中情况。这样一来我们统计重复的情况即 即统计了 (a,b) 又统计了 (b,a)所以我们得将结果除以2,但是 a,b全是LCM的情况我们只统计了一次,所以我们还得加上1
代码如下:

1 #include <algorithm> 2 #include <queue> 3 #include <cstdio> 4 #include <iostream> 5 #include <cstring> 6 #include <map> 7 #include <cmath> 8 using namespace std; 9 10 typedef long long LL; 11 const int maxn = 1000; 12 LL u[maxn], cnt; 13 14 bool fenjie(LL n){ 15 LL f = (LL) sqrt(n+0.5); 16 bool isprimer = true; 17 for(int i = 2; i <= n; ++i) { 18 if(i > f && isprimer) return true; 19 if(n%i == 0) { 20 u[cnt] = 0; 21 while(n%i == 0) { 22 isprimer = false; 23 u[cnt]++; 24 n /= i; 25 } 26 cnt++; 27 } 28 } 29 return false; 30 } 31 32 int main(){ 33 // freopen("out.txt", "w", stdout); 34 // freopen("in.txt", "r", stdin); 35 LL n, ans; 36 while(cin >> n && n) { 37 cnt = 0; 38 if(fenjie(n)) { 39 cout << n << " " << 2 << endl; 40 continue; 41 } 42 ans = 1; 43 for(int i = 0; i < cnt; ++i){ 44 ans *= (2*u[i] + 1); 45 } 46 ans = ans/2 + 1; 47 cout << n << " " << ans << endl; 48 } 49 return 0; 50 }
标签:src bsp namespace queue sof one while continue soft
原文地址:https://www.cnblogs.com/DynastySun/p/9368282.html