标签:效果 计算 shift 方差 blog width 角度 blank 变换
1、Batch Normalization的引入
在机器学习领域有个很重要的假设:IID独立同分布假设,也就是假设训练数据和测试数据是满足相同分布的,这是通过训练数据获得的模型能够在测试集上获得好的效果的一个基本保障。在深度学习网络中,后一层的输入是受前一层的影响的,而为了方便训练网络,我们一般都是采用Mini-Batch SGD来训练网络的(Mini-Batch SGD的两个优点是:梯度更新方向更准确和并行计算速度快)。
我们知道在神经网络训练开始前,都要对输入数据做一个归一化处理,那么具体为什么需要归一化呢?归一化后有什么好处呢?原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。
我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。nternal指的是深层网络的隐层,是发生在网络内部的事情,而不是covariate shift问题只发生在输入层。Batch Normalization就是来解决该问题的。Batch Normalization的基本思想就是能不能让每个隐层节点的激活输入分布固定下来,从而避免Internal Covariate Shift的问题。
2、Batch Normalization的本质思想
就像激活函数层、卷积层、全连接层、池化层一样,BN(Batch Normalization)也属于网络的一层。BN的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值(就是那个x=WU+B,U是输入)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值WU+B是大的负值或正值),所以这导致后向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因,而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
首先我们来看下期望为0,方差为1的标准正态分布:
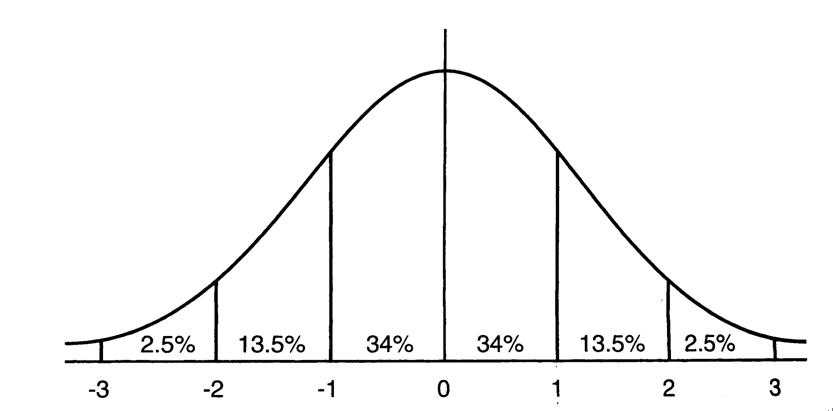
这意味着在一个标准差范围内,也就是说64%的概率x其值落在[-1,1]的范围内,在两个标准差范围内,也就是说95%的概率x其值落在了[-2,2]的范围内。我们知道,激活值x=WU+B,U是真正的输入,x是某个神经元的激活值,假设非线性函数是sigmoid,那么看下sigmoid函数及其导数如下:
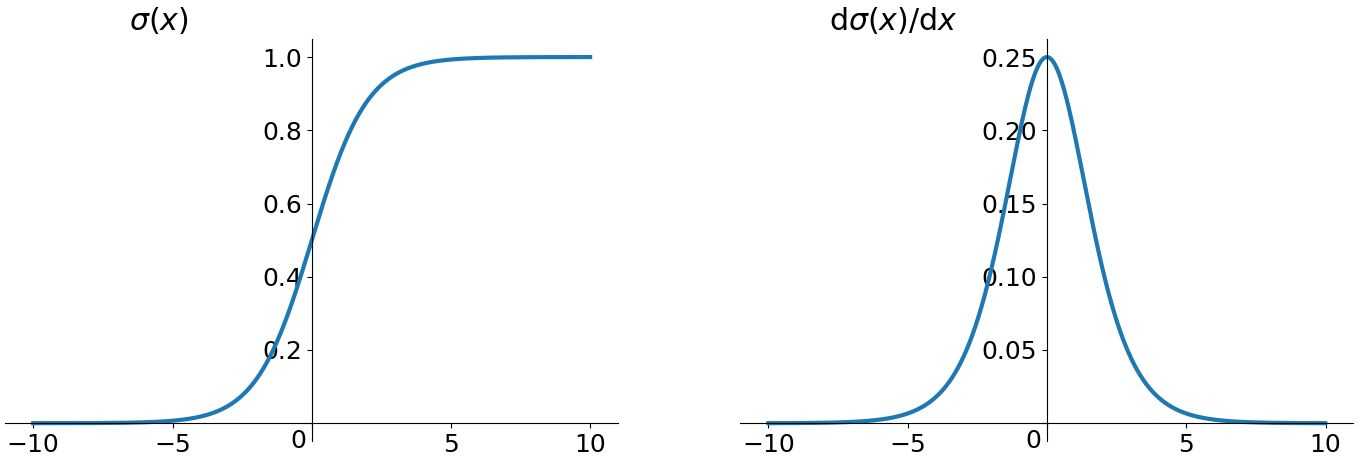
我们可以从中观察到,sigmoid函数的导数范围是(0, 0.25]。假设没有经过BN调整前x的原先正态分布均值是-6,方差是1,那么意味着95%的值落在了[-8, -4]之间,那么对应的Sigmoid函数值及其导数的值都明显接近于0,这是典型的梯度饱和区,在这个区域里梯度变化很慢,导数接近于0意味着梯度变化很小甚至消失。而假设经过BN后,均值是0,方差是1,那么意味着95%的x值落在了[-2, 2]区间内,很明显这一段是sigmoid(x)函数接近于线性变换的区域,意味着x的小变化会导致非线性函数值较大的变化,也即是梯度变化较大,对应导数函数图中明显大于0的区域,就是梯度非饱和区。
这种性质不只是适用于sigmoid函数,也适用于其他的激活函数。而且从图中经过BN后,使得大部分的激活值落入非线性函数的线性区内(也就是在0附近的那一段,很多激活函数都有这样的性质),在这里对应的导数远离导数饱和区,这样来加速训练收敛过程。
但是从上面来看,把大部分激活值拉入到线性区,也就相当于在网络的传输过程中对输入值做了一系列的线性变换,那么此时网络的表达能力急剧下降,而且深层也没有意义(多层的线性转换和一层的线性转换是一样的)。为了解决这个问题,BN对标准化后的值X又进行了scale加上shift操作(y=scale*x+shift)。对每个神经元增加了两个参数scale和shift参数,这两个参数是通过训练学习到的,意思是通过scale和shift把这个值从标准正态分布左移或者由移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。这样看似之前的标准化变换毫无意义,又回到了起点。其实不然,大神博主张俊林认为:这种做法的核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。这种想法看似是有一定的道理的,尽量保证激活值在非线性区域,而又不会进入到梯度饱和区。
3、Batch Normalization算法
Batch Normalization操作就像激活函数层、卷积层、全连接层、池化层一样,也属于网络中的一层。我们要对每个隐层神经元的激活值做BN,那么就可以想象成每个隐层又加上了一层BN操作层,它位于X=WU+B激活值获得之后,非线性函数变换之前,其图示如下:
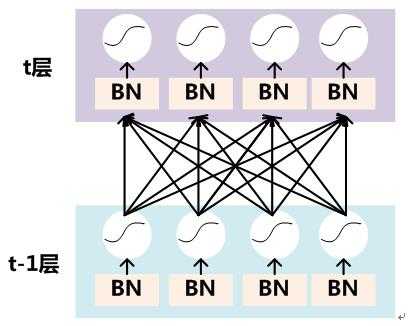
具体BN网络层的前向传播过程如下
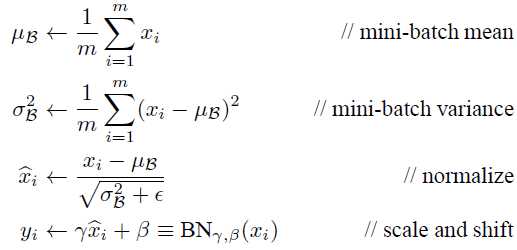
在这里的期望μB是每一次Mini-Batch SGD时的Mini-Batch的均值,σB2也是Mini-Batch的方差。
在做验证或者测试时只有一个样本的输入,此时没有Mini-Batch,那么怎么计算标准化的期望和方差呢?在训练的过程中我们会将每一次梯度下降时的Mini-Batch的期望和方差保存起来,在验证和测试时我们就用这些保存的期望和方差的期望值来作为此时的期望和方差(这句话有点拗口,其实就是在训练过程中会计算很多批Mini-Batch的期望和方差,在之后的验证和测试的时候,我们将这批Mini-Batch的期望和方差分别求平均值来作为此时的期望和方差)。具体算法流程如下:
![]()
![]()
在得到了均值和方差之后的计算和训练时计算公式有点不一样(也只是表现形式不一样,本质和训练时是一样的):
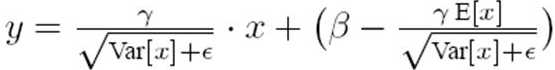
至于为什么要写成上述形式,可能是为了减少计算量,因为在实际的验证和测试时我们的γ、β、μ和σ值都是已经确实的,这样在一开始就求出
![]()
然后保存起来,这样就避免了重复计算的过程。
4、Batch Normalization的优点
1)你可以选择比较大的初始学习率,让你的训练速度飙涨。以前还需要慢慢调整学习率,甚至在网络训练到一半的时候,还需要想着学习率进一步调小的比例选择多少比较合适,现在我们可以采用初始很大的学习率,然后学习率的衰减速度也很大,因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率,也比以前的收敛速度快,因为它具有快速训练收敛的特性。
2)你再也不用去理会过拟合中drop out、L2正则项参数的选择问题,采用BN算法后,你可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性。
3)再也不需要使用使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法),因为BN本身就是一个归一化网络层。
4)可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到,文献说这个可以提高1%的精度,这句话我也是百思不得其解啊)。
5、Batch Normalization在CNN中的应用
BN在CNN中的应用也同样采用共享权值的操作,把一个FilterMap看成一个整体,可以想象成是一个Filter Map对应DNN隐层中的一个神经元,所以一个Filter Map的所有神经元共享一个Scale和Shift参数,Mini-Batch里m个实例的统计量均值和方差是在p*q个神经元里共享,就是说从m*p*q个激活里面算Filter Map全局的均值和方差,这体现了Filter Map的共享参数特性,当然在实际计算的时候每个神经元还是各算各的BN转换值,只不过采用的统计量和Scale,shift参数用的都是共享的同一套值而已。
6、Batch Normalization在RNN中的应用
对于RNN来说,希望引入BN的一个很自然的想法是在时间序列方向展开的方向,即水平方向(图1)在隐层神经元节点引入BN,因为很明显RNN在时间序列上展开是个很深的深层网络,既然BN在深层DNN和CNN都有效,很容易猜想这个方向很可能也有效。
另外一个角度看RNN,因为在垂直方向上可以叠加RNN形成很深的Stacked RNN,这也是一种深层结构,所以理论上在垂直方向也可以引入BN,也可能会有效。但是一般的直觉是垂直方向深度和水平方向比一般深度不会太深,所以容易觉得水平方向增加BN会比垂直方向效果好。
然而关于上面两种用法还是有很多争议,不一定都能有好的结果,具体的结论可能如下:
1)RNN垂直方向引入BN的话:如果层数不够深(感觉5层是各分界线),那么BN的效果不稳定或者是有损害效果,如果深度足够的话,是能够加快训练收敛速度和泛化性能的。
2)在隐层节点做BN的话:
![]()
就是对水平序和垂直序单独做BN,然后再相加。
3)在水平方向做BN时,因为RNN在不同时间点水平展开后参数共享的,所以就产生了BN在不同时间序列的参数也是共享的,事实证明这是不行的。因此BN在RNN中在每个时间点神经元上必须维护各自的统计量和参数。
4)在水平方向做BN时,Scala参数要足够小,一般设置为0.1是可以的。
参考文献:
深度学习(二十九)Batch Normalization 学习笔记
[深度学习] Batch Normalization算法介绍
标签:效果 计算 shift 方差 blog width 角度 blank 变换
原文地址:https://www.cnblogs.com/jiangxinyang/p/9372678.html