标签：pop   技术分享   超过   alt   说明   反向   算法实现   算法   好的   

网络流 ———— 从零开始（的异世界）

（更好的阅读体验：https://www.zybuluo.com/Yeasion-Nein/note/1228060）

首先，我们要知道什么是网络流，我们可以类比水流在水管里面的流动，假设在一个类似于有向图中的水管道中，有一个自来水厂\(S\)点，里面有源源不断的自来水流出，然后在另一个\(T\)点有一个基饥♂渴的人正在等待着喝水，他已经\(0x7fffffff\)年没有喝过水啦，所以我们要想办法能让他喝到尽可能多的水。我们知道，每一根管子都有各自的粗♂细，也就是容量，从S点流出的流量不能超过这条路径上的任意一条边的容量，不然管子就会爆掉的。

而求这个人能够喝到的水的最大量就是最大流问题。这个\(S\)点称为源点，这个\(T\)点称为汇点，这样的图就叫做网络流。

比如下面这个图的最大流就是\(1\)+\(2\)+\(2\)=\(5\)。

要注意：一个图的最大流路径并不是只有一个（有例外啦），比如上图在上方就是\(1\)，中间就是\(2\)，下方也是\(2\)，然后才总汇成了最大流\(5\)。

然后是可行流，就是假如所有边上的流量都没有超过容量，那么这一组流称为一组可行流，而很显然，一个网络流的最大流就是所有可行流中流量最大的一种。然后可行流中最简单的就是零流。也就是流量为\(0\)啦。

然后对于求最大流的算法，这里；列举出了两种：

1：\(EK\)算法 (\(Edmonds-Karp\))

首先，我们从最简单的零流开始，假设我们搜索到了一条路径\(A\)，从源点可以到达汇点，即A:{\(S\)->\(a1\)->\(a2\)->...->\(T\)},然后要注意，这条路上的每一条边满足的条件是流量<容量。并不是<=，因为这样会造成程序死循环。

然后我们可以找到这条路上的每一条边的剩余量的最小值\(rest\)，就是说我这个流的每一条边都有这\(rest\)的容量剩余，那么显而易见，我们将这条路上的所有边的流量都加上\(rest\)仍然是一个可行流。

就这样，我们找到了一个比一开始的流更大的流，也就是之前的流量+\(rest\)，我们称这条路为增广路。我们从\(S\)开始不断地寻找增广路，每次增广候我们都会得到一个比原来更大的流。这也就是为什么之前的流量是严格小于容量的，如果是=的话，程序就会一直寻找到\(rest\)的最小值为\(0\)，就会形成死循环。

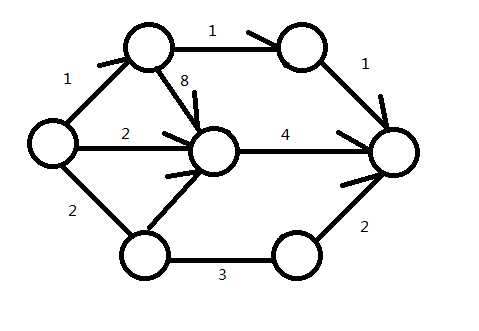
而当找不到增广路的时候，当前的流就是最大流了。

然后具体的算法实现还是有些东西的。举一个已经用烂了的例子来说明吧。

在这里，我们假设傻傻的程序先找到了\(1\)->\(2\)->\(3\)->\(4\)这条路径，我们就会发现程序找出来的最大流为\(1\)，然后更改{\(1\)->\(2\)}、{\(2\)->\(3\)}、{\(3\)->\(4\)}的\(rest\)为\(0\)。

然而我们能很明显的看出来如果流{\(1\)->\(2\)->\(4\)}、{\(1\)->\(3\)->\(4\)}的话，能够得到更大的流量2，于是我们就知道这个程序是有问题的咯。所以我们反思：为什么会出错呢？

答案就是：你可能很聪明，一眼就看出来怎么走，但是程序是傻的，它只会按照你给的机制跑，但是很无奈你并没有给它一个反悔的机制，于是就凉凉了~

在这里我们采用加反向边的做法，对每一条{\(a[i]->a[j]\)}都建一条容量为\(0\)的反向边{\(a[j]->a[i]\)}。然后整个图建完是这样的：

我们在每一次找到增广路的时候会将每一段的容量减少\(rest\)，同时我们也将这些反向边容量增加\(rest\)。即：

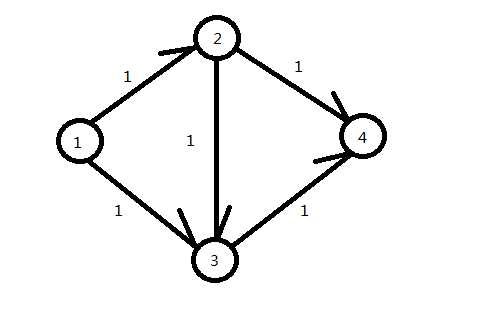
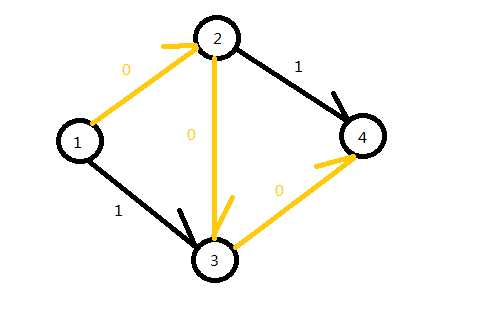
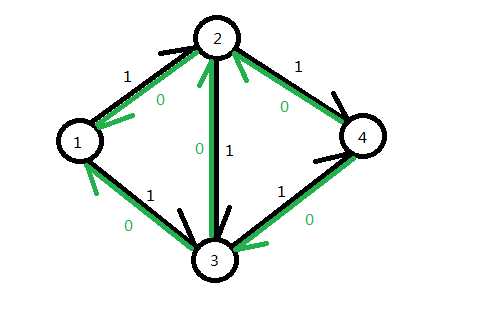
\(cap[a[i]][a[j]]\)-=\(rest\); \(cap[a[j]][a[i]]\)+=\(rest\);

然后按刚才的方法我们先找到了\(1\)->\(2\)->\(3\)->\(4\),然后更改为：

。

然后我们再次寻找增广路，找到\(1\)->\(3\)->\(2\)->\(4\),\(rest\)为\(1\)，再次增广之后，我们得到了最大流2。就相当与是把流进来的\(2\)->\(4\)又给退了回去，最后结果就是选了\(1\)->\(2\)->\(4\)、\(1\)->\(3\)->\(4\)。这就是原由。

而这个网络流版本就是\(EK\)算法。

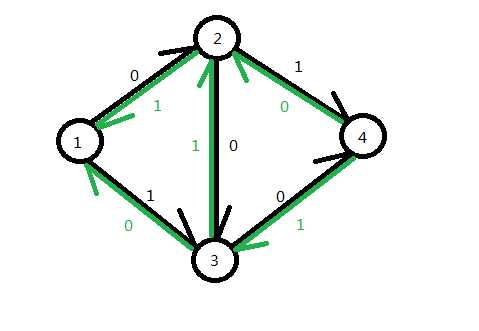#define MAXN 100010
#define INF 0x7fffffff
bool visit[MAXN];
int pre[MAXN];
queue<int> q;
void update(int now,int rest){
    while(pre[now]){
        map[pre[now]][now]-=rest;//正向的-=rest 
        map[now][pre[now]]+=rest;//负向的+=rest 
        now=pre[now];
    }
}
int find(int S,int T){//寻找增广路流量 
    memset(visit,0,sizeof(visit));
    memset(pre,-1,sizeof(pre));
    visit[S]=1; int minn=INF;
    q.push(S);
    while(!q.empty()){
        int now=q.front(); q.pop();
        if(now==t) break;
        for(int i=1;i<=m;i++){
            if(!visit[i]&&MAP[now][i]){
                q.push(i);
                minn=min(minn,map[now][i]);//最小的rest 
                pre[i]=now; visit[i]=1;
            }
        } 
    }
    if(pre[i]==-1) return 0;
    return minn;
}
int EK(int S,int T){ //EK算法主体 
    int new_flow=0;//增广路的流量 
    int max_flow=0;//最大流 
    do{
        new_flow=find(S,T);
        update(T,new_flow);
        max_flow+=new_flow;
    }while(new_flow);
    return max_flow;
}

恩，\(EK\)算法差不多就是这个样子。

网络流 ———— 从零开始

标签：pop   技术分享   超过   alt   说明   反向   算法实现   算法   好的   

原文地址：https://www.cnblogs.com/Yeasio-Nein/p/Flow.html