标签:也会 综合 oat 整理 length sof family 完成 title
在上一节我们已经介绍了如何对相机进行标定。然后获取相机的内部参数,外部参数。
内参包括焦距、主点、倾斜系数、畸变系数
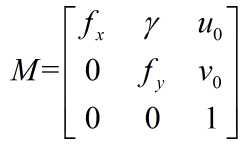
其中γ为坐标轴倾斜参数,理想情况下为0。
外参包括旋转矩阵R、平移向量T,它们共同描述了如何把点从世界坐标系转换到摄像机坐标系,旋转矩阵描述了世界坐标系的坐标轴相对于摄像机坐标轴的方向,平移向量描述了在摄像机坐标系下空间原点的位置。
人类可以看到3维立体的世界,是因为人的两只眼睛,从不同的方向看世界,两只眼睛中的图像的视差,让我们可以看到三维立体的世界。类似的,要想让计算机“看到”三维世界,就需要使用至少两个摄像头构成双目立体视觉系统。
这里我们想要通过获取三维空间物体的坐标有两种方法,下面会介绍。
cv::Mat mapx = cv::Mat(imageSize, CV_32FC1); cv::Mat mapy = cv::Mat(imageSize, CV_32FC1); cv::Mat R = cv::Mat::eye(3, 3, CV_32F); std::cout << "显示矫正图像" << endl; for (int i = 0; i != imageCount; i++) { std::cout << "Frame #" << i + 1 << "..." << endl; //计算图片畸变矫正的映射矩阵mapx、mapy(不进行立体校正,立体校正需要利用双摄) initUndistortRectifyMap(cameraMatrix, distCoeffs, R, cameraMatrix, imageSize, CV_32FC1, mapx, mapy); //读取一张图片 Mat imageSource = imread(filenames[i]); Mat newimage = imageSource.clone(); //另一种不需要转换矩阵的方式 //undistort(imageSource,newimage,cameraMatrix,distCoeffs); //进行校正 remap(imageSource, newimage, mapx, mapy, INTER_LINEAR); imshow("原始图像", imageSource); imshow("矫正后图像", newimage); waitKey(); }
上一节我们介绍了从世界坐标系到像素坐标系的转换:
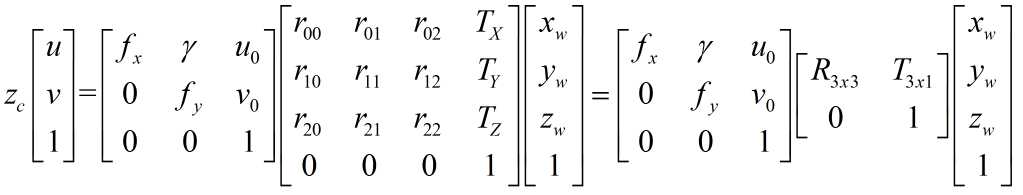
其中[u v 1]T为矫正后的图像中的点在像素坐标系中的坐标,[xw yw zw 1]T为点在世界坐标系中的坐标。
现在我们来研究一下从像素坐标系到世界坐标系的转换:
光轴会聚模型(两个摄像机的像平面不是平行的):
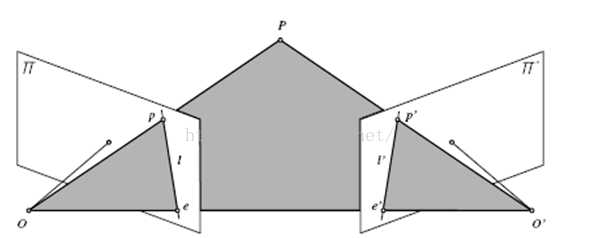
对于左右相机分别有:
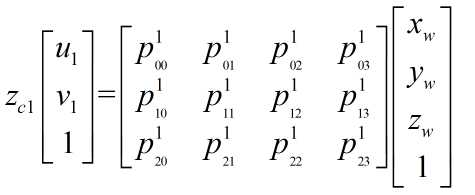
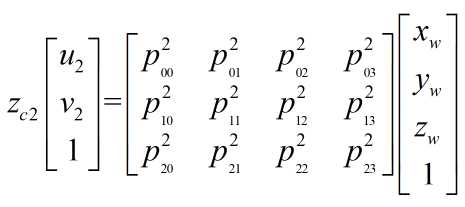
将上面两式整理可以得到:
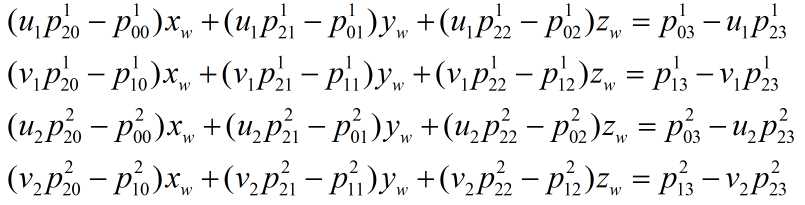
采用最小二乘法求解X,Y,Z,在opencv中可以用solve(A,B,XYZ,DECOMP_SVD)求解:
代码如下(来源于网上):
//opencv2.4.9 vs2012 #include <opencv2\opencv.hpp> #include <fstream> #include <iostream> using namespace std; using namespace cv; Point2f xyz2uv(Point3f worldPoint,float intrinsic[3][3],float translation[1][3],float rotation[3][3]); Point3f uv2xyz(Point2f uvLeft,Point2f uvRight); //图片对数量 int PicNum = 14; //左相机内参数矩阵 float leftIntrinsic[3][3] = {4037.82450, 0, 947.65449, 0, 3969.79038, 455.48718, 0, 0, 1}; //左相机畸变系数 float leftDistortion[1][5] = {0.18962, -4.05566, -0.00510, 0.02895, 0}; //左相机旋转矩阵 float leftRotation[3][3] = {0.912333, -0.211508, 0.350590, 0.023249, -0.828105, -0.560091, 0.408789, 0.519140, -0.750590}; //左相机平移向量 float leftTranslation[1][3] = {-127.199992, 28.190639, 1471.356768}; //右相机内参数矩阵 float rightIntrinsic[3][3] = {3765.83307, 0, 339.31958, 0, 3808.08469, 660.05543, 0, 0, 1}; //右相机畸变系数 float rightDistortion[1][5] = {-0.24195, 5.97763, -0.02057, -0.01429, 0}; //右相机旋转矩阵 float rightRotation[3][3] = {-0.134947, 0.989568, -0.050442, 0.752355, 0.069205, -0.655113, -0.644788, -0.126356, -0.753845}; //右相机平移向量 float rightTranslation[1][3] = {50.877397, -99.796492, 1507.312197}; int main() { //已知空间坐标求像素坐标 Point3f point(700,220,530); cout<<"左相机中坐标:"<<endl; cout<<xyz2uv(point,leftIntrinsic,leftTranslation,leftRotation)<<endl; cout<<"右相机中坐标:"<<endl; cout<<xyz2uv(point,rightIntrinsic,rightTranslation,rightRotation)<<endl; //已知左右相机像素坐标求空间坐标 Point2f l = xyz2uv(point,leftIntrinsic,leftTranslation,leftRotation); Point2f r = xyz2uv(point,rightIntrinsic,rightTranslation,rightRotation); Point3f worldPoint; worldPoint = uv2xyz(l,r); cout<<"空间坐标为:"<<endl<<uv2xyz(l,r)<<endl; system("pause"); return 0; } //************************************ // Description: 根据左右相机中像素坐标求解空间坐标 // Method: uv2xyz // FullName: uv2xyz // Access: public // Parameter: Point2f uvLeft // Parameter: Point2f uvRight // Returns: cv::Point3f // Author: 小白 // Date: 2017/01/10 // History: //************************************ Point3f uv2xyz(Point2f uvLeft,Point2f uvRight) { // [u1] [xw] [u2] [xw] //zc1 *|v1| = Pl*[yw] zc2*|v2| = P2*[yw] // [ 1] [zw] [ 1] [zw] // [1 ] [1 ] Mat mLeftRotation = Mat(3,3,CV_32F,leftRotation); Mat mLeftTranslation = Mat(3,1,CV_32F,leftTranslation); Mat mLeftRT = Mat(3,4,CV_32F);//左相机RT矩阵 hconcat(mLeftRotation,mLeftTranslation,mLeftRT); Mat mLeftIntrinsic = Mat(3,3,CV_32F,leftIntrinsic); Mat mLeftP = mLeftIntrinsic * mLeftRT; //cout<<"左相机P矩阵 = "<<endl<<mLeftP<<endl; Mat mRightRotation = Mat(3,3,CV_32F,rightRotation); Mat mRightTranslation = Mat(3,1,CV_32F,rightTranslation); Mat mRightRT = Mat(3,4,CV_32F);//右相机RT矩阵 hconcat(mRightRotation,mRightTranslation,mRightRT); Mat mRightIntrinsic = Mat(3,3,CV_32F,rightIntrinsic); Mat mRightP = mRightIntrinsic * mRightRT; //cout<<"右相机P矩阵 = "<<endl<<mRightP<<endl; //最小二乘法A矩阵 Mat A = Mat(4,3,CV_32F); A.at<float>(0,0) = uvLeft.x * mLeftP.at<float>(2,0) - mLeftP.at<float>(0,0); A.at<float>(0,1) = uvLeft.x * mLeftP.at<float>(2,1) - mLeftP.at<float>(0,1); A.at<float>(0,2) = uvLeft.x * mLeftP.at<float>(2,2) - mLeftP.at<float>(0,2); A.at<float>(1,0) = uvLeft.y * mLeftP.at<float>(2,0) - mLeftP.at<float>(1,0); A.at<float>(1,1) = uvLeft.y * mLeftP.at<float>(2,1) - mLeftP.at<float>(1,1); A.at<float>(1,2) = uvLeft.y * mLeftP.at<float>(2,2) - mLeftP.at<float>(1,2); A.at<float>(2,0) = uvRight.x * mRightP.at<float>(2,0) - mRightP.at<float>(0,0); A.at<float>(2,1) = uvRight.x * mRightP.at<float>(2,1) - mRightP.at<float>(0,1); A.at<float>(2,2) = uvRight.x * mRightP.at<float>(2,2) - mRightP.at<float>(0,2); A.at<float>(3,0) = uvRight.y * mRightP.at<float>(2,0) - mRightP.at<float>(1,0); A.at<float>(3,1) = uvRight.y * mRightP.at<float>(2,1) - mRightP.at<float>(1,1); A.at<float>(3,2) = uvRight.y * mRightP.at<float>(2,2) - mRightP.at<float>(1,2); //最小二乘法B矩阵 Mat B = Mat(4,1,CV_32F); B.at<float>(0,0) = mLeftP.at<float>(0,3) - uvLeft.x * mLeftP.at<float>(2,3); B.at<float>(1,0) = mLeftP.at<float>(1,3) - uvLeft.y * mLeftP.at<float>(2,3); B.at<float>(2,0) = mRightP.at<float>(0,3) - uvRight.x * mRightP.at<float>(2,3); B.at<float>(3,0) = mRightP.at<float>(1,3) - uvRight.y * mRightP.at<float>(2,3); Mat XYZ = Mat(3,1,CV_32F); //采用SVD最小二乘法求解XYZ solve(A,B,XYZ,DECOMP_SVD); //cout<<"空间坐标为 = "<<endl<<XYZ<<endl; //世界坐标系中坐标 Point3f world; world.x = XYZ.at<float>(0,0); world.y = XYZ.at<float>(1,0); world.z = XYZ.at<float>(2,0); return world; } //************************************ // Description: 将世界坐标系中的点投影到左右相机像素坐标系中 // Method: xyz2uv // FullName: xyz2uv // Access: public // Parameter: Point3f worldPoint // Parameter: float intrinsic[3][3] // Parameter: float translation[1][3] // Parameter: float rotation[3][3] // Returns: cv::Point2f // Author: 小白 // Date: 2017/01/10 // History: //************************************ Point2f xyz2uv(Point3f worldPoint,float intrinsic[3][3],float translation[1][3],float rotation[3][3]) { // [fx γ u0] [xc] [xw] [u] [xc] //M = |0 fy v0| TEMP = [R T] |yc| = TEMP*[yw] zc*[v] = M*[yc] // [ 0 0 1 ] [zc] [zw] [1] [zc] // [1 ] Point3f c; c.x = rotation[0][0]*worldPoint.x + rotation[0][1]*worldPoint.y + rotation[0][2]*worldPoint.z + translation[0][0]*1; c.y = rotation[1][0]*worldPoint.x + rotation[1][1]*worldPoint.y + rotation[1][2]*worldPoint.z + translation[0][1]*1; c.z = rotation[2][0]*worldPoint.x + rotation[2][1]*worldPoint.y + rotation[2][2]*worldPoint.z + translation[0][2]*1; Point2f uv; uv.x = (intrinsic[0][0]*c.x + intrinsic[0][1]*c.y + intrinsic[0][2]*c.z)/c.z; uv.y = (intrinsic[1][0]*c.x + intrinsic[1][1]*c.y + intrinsic[1][2]*c.z)/c.z; return uv; }
上面的代码看起来可以实现从像素坐标到三维空间坐标的转换。但是实际上会存在一个问题,假设世界坐标系中的点在左像平面的投影坐标为p1,你如何找到该点在右像平面的投影坐标p2,虽然现在有很多图片匹配算法比如SDA,BM,SGBM等,但是如果我们直接在右像平面的二维空间中逐个像素的取搜索匹配点,这个效率是非常低的。因此我们提出了利用极点约束,实现把二维空间匹配降维到一维匹配,这样就加快了运算的速度,这也是我下面将要介绍到的内容立体校正。
matlab或者opencv标定完都是在左相机上建立世界坐标系,于是上面代码对应的改为:
//左相机旋转矩阵 float leftRotation[3][3] = {1,0,0, 0,1,0, 0,0,1 }; //左相机平移向量 float leftTranslation[1][3] = {0,0,0};
假设我们已经完成了对两个摄像头的单目标定,并且得到了左右摄像摄像机坐标系相对同一世界坐标系的旋转矩阵和平移矩阵,然后我们就可以获取两个摄像头之间的相对位置关系,这也就是我们经常所说的双目标定(或者叫双目立体标定)。
双目摄像机需要标定的参数:摄像机内参数矩阵M,畸变系数矩阵,本征矩阵E,基础矩阵F,旋转矩阵R以及平移矩阵t(其中摄像机内参数矩阵和畸变系数矩阵可以通过单目标定的方法标定出来)
双目摄像机标定和单目摄像机标定最主要的区别就是双目摄像机需要标定出左右摄像机坐标系之间的相对关系。
我们用旋转矩阵R和平移矩阵T来描述左右两个摄像机坐标系的相对关系,具体为:在左相机上建立世界坐标系。
假设空间中有一点P,其在世界坐标系下的坐标为Pw,其在左右摄像机坐标系下的坐标可以表示为:
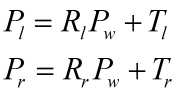
其中Pl和Pr又有如下的关系:
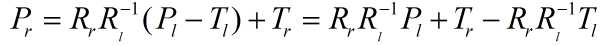
综合上式,可以推得:
![]()
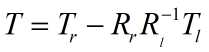
其中Rl,Tl为左摄像头经过单目标定得到的相对标定物的旋转矩阵和平移向量,Rr,Tr为右摄像头经过单目标定得到的相对标定物的旋转矩阵和平移向量。
左右相机分别进行单目标定,就可以分别Rl,Tl,Rr,Tr。带入上式就可以求出左右相机之间的旋转矩阵R和平移T。
注意:因为旋转矩阵R、Rl、Rr均是单位正交矩阵。正交矩阵的逆(inverse)等于正交矩阵的转置(transpose)。
单目摄像机需要标定的参数,双目都需要标定,双目摄像机比单目摄像机多标定的参数:R和T,主要是描述两个摄像机相对位置关系的参数,这些参数在立体校正和对极几何中用处很大
那么得到了立体标定的结果,下一步我们就该进行立体校正。
在介绍立体校正的具体方法之前,让我们来看一下,为什么要进行立体校正?
双目摄像机系统主要的任务就是测距,而视差求距离公式是在双目系统处于理想情况下推导的,但是在现实的双目立体视觉系统中,是不存在完全的共面行对准的两个摄像机图像平面的。所以我们要进行立体校正。立体校正的目的就是,把实际中消除畸变后的非共面行对准的两幅图像,校正成共面行对准。(共面行对准:两摄像机图像平面在同一平面上,且同一点投影到两个摄像机图像平面时,两个像素坐标系的同一行,这样图片匹配时速度就会有很大的提升),将实际的双目系统校正为理想的双目系统。
理想双目系统:两摄像机图像平面平行,光轴和图像平面垂直,极点处于无穷远处,此时点(x0,y0)对应的级线就是y=y0。
立体校正前:
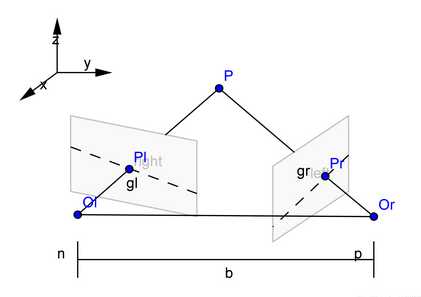
立体校正后:
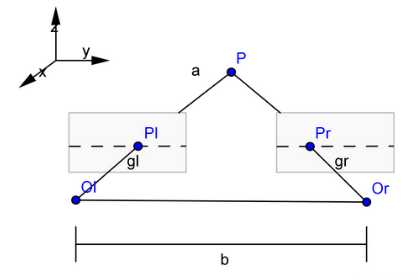
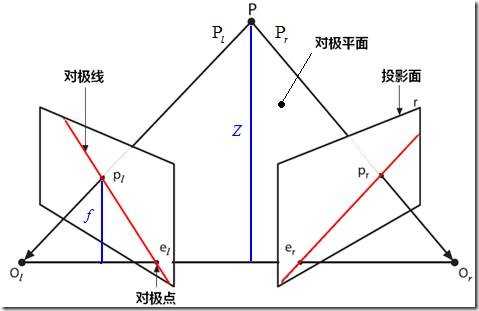
上面两张图中可以看到,立体校正前的左右相机的光心并不是平行的,两个光心的连线就叫基线,像平面与基线的交点就是极点,像点与极点所在的直线就是极线,左右极线与基线构成的平面就是空间点对应的极平面。
校正后,极点在无穷远处,两个相机的光轴平行。像点在左右图像上的高度一致。这也就是极线校正的目标。校正后做后续的立体匹配时,只需在同一行上搜索左右像平面的匹配点即可,能使效率大大提高。
Bouguet的方法,是将旋转矩阵R和平移矩阵T分解成左右相机各旋转一半的旋转和平移矩阵Rl,Tl与Rr,Tr。分解的原则是使得,左右图像重投影造成的畸变最小,左右视图的共同面积最大。
1、将右图像平面相对于左图像平面的旋转矩阵分解成两个矩阵Rl和Rr,叫做左右相机的合成旋转矩阵。
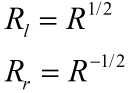
其中R1/2*R1/2=R,R-1/2是R1/2的逆矩阵。
2、将左右相机各旋转一半,使得左右相机的光轴平行。此时左右相机的成像面达到平行,但是基线与成像平面不平行。
3、构造变换矩阵Rrect使得基线与成像平面平行。构造的方法是通过右相机相对于左相机的偏移矩阵T完成的。
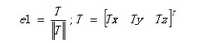
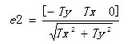
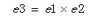
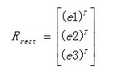
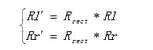
OpenCV提供了函数cvStereoCalibrate,用来进行双目标定,直接通过cvStereoCalibrate来实现双目定标,很容易产生比较大的图像畸变,边角处的变形较厉害。最好先通过cvCalibrateCamera() 对每个摄像头单独进行定标,再利用cvStereoCalibrate进行双目定标。这样定标所得参数才比较准确,随后的校正也不会有明显的畸变。
/* 进行立体双目标定 由于左右摄像机分别都经过了单目标定 所以在此处选择flag = CALIB_USE_INTRINSIC_GUESS */ double rms = stereoCalibrate(objRealPoint, //vector<vector<point3f>> 型的数据结构,存储标定角点在世界坐标系中的位置 imagePointL, //vector<vector<point2f>> 型的数据结构,存储标定角点在第一个摄像机下的投影后的亚像素坐标 imagePointR, //vector<vector<point2f>> 型的数据结构,存储标定角点在第二个摄像机下的投影后的亚像素坐标 cameraMatrixL, //输入/输出型的第一个摄像机的相机矩阵。如果CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO ,CV_CALIB_FIX_INTRINSIC , or CV_CALIB_FIX_FOCAL_LENGTH其中的一个或多个标志被设置,该摄像机矩阵的一些或全部参数需要被初始化 distCoeffL, //第一个摄像机的输入/输出型畸变向量。根据矫正模型的不同,输出向量长度由标志决定 cameraMatrixR, //输入/输出型的第二个摄像机的相机矩阵。参数意义同第一个相机矩阵相似 distCoeffR, //第一个摄像机的输入/输出型畸变向量。根据矫正模型的不同,输出向量长度由标志决定 Size(imageWidth, imageHeight), //图像的大小 R, //输出型,第一和第二个摄像机之间的旋转矩阵 T, //输出型,第一和第二个摄像机之间的平移矩阵 E, //输出本征矩阵 F, //输出基础矩阵 CALIB_USE_INTRINSIC_GUESS, TermCriteria(TermCriteria::COUNT + TermCriteria::EPS, 100, 1e-5));
上面的cameraMatrixL(R),distCoeffL(R) 分别是单目定标后获得的左(右)摄像头的内参矩阵(3*3)和畸变参数向量(1*5或者5*1);R, T 分别是双目立体标定获取的右摄像头相对于左摄像头的旋转矩阵(3*3)和平移向量(3*1), E是包含了两个摄像头相对位置关系的本征矩阵Essential Matrix(3*3),F 则是既包含两个摄像头相对位置关系、也包含摄像头各自内参信息的基础矩阵(3*3)。

对极几何在双目问题中非常的重要,可以简化立体匹配等问题,而要应用对极几何去解决问题,比如求极线,需要知道本征矩阵或者基础矩阵,因此双目标定过程中也会把本征矩阵和基础矩阵算出来。
cvStereoCalibrate 是怎样计算 Essential Matrix 和 Fundamental Matrix 的?
(1)Essential Matrix
本征矩阵常用字母E来表示,其物理意义是左右图像坐标系相互转换的矩阵,描述的是同一空间点投影在左右摄像机图像平面上对应点之间的关系,单位为mm。
给定一个目标点P,以左摄像头光心Ol为世界坐标系原点,其在世界坐标系下的坐标为Pw,其在左右摄像机坐标系下的坐标分别为Pcl和Pcr,右摄像机坐标系原点在左摄像机坐标系的坐标为T=[Tx,Ty,Tz]T,则有:
![]()
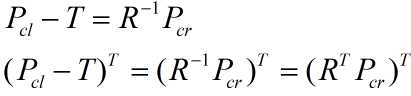
则通过点T的所有点所组成的平面(即极面)可以用下式表示:
![]()
向量的叉积又可表示为矩阵与向量的乘积:
![]()
注意:上面的运算符号x表示向量之间的叉乘运算,运算符号.表示两个向量的点乘。
其中S:
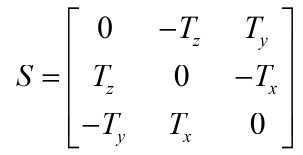
综合上式可得:
![]()
乘积RS即为本征矩阵E,令E=RS,得到:
![]()
描述了同一物理点在左右摄像机图像平面上投影在相机坐标系下的关系。
(2)Fundamental Matrix
由于矩阵E并不包含摄像头内参信息,且E是面向摄像头坐标系的。实际上我们更感兴趣的是在像素坐标系上去研究一个像素点在另一视图上的对极线,这就需要用到摄像机的内参信息将摄像机坐标系和像素坐标系联系起来。我们定义基础矩阵F,描述同一物理点在左右摄像机像素坐标系下的关系,单位为pix。
像素坐标系与摄相机坐标系的关系:
![]()
![]()
假设左右摄像机坐标系下点Pcl、Pcr 在像素坐标系中对应的坐标分别为 Ppixl、Ppixr ,我们可以得到:
![]()
由此可将基础矩阵F定义为:
![]()
最终得到同一物理点在左右摄像机像素坐标系下的关系:
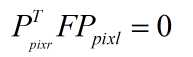
标签:也会 综合 oat 整理 length sof family 完成 title
原文地址:https://www.cnblogs.com/zyly/p/9373991.html