码迷，mamicode.com
首页 > 其他好文 > 详细

【数据结构】【平衡树】Treap

时间：2018-07-29 00:49:16      阅读：123      评论：0      收藏：0      [点我收藏+]

标签：节点   改变   手写   模板   考题   程序   调用   大于   思考   

百度百科

Pre_knowledge

　　　　二叉排序树

　　　　二叉排序树是一棵二叉树。每个节点对应一个权值v，对于每个节点，一定满足如下性质：

　　　　　　　　二叉排序树的每个节点的左子树要么为空，要么左子树的任意节点的权值v‘一定小于v。

　　　　　　　　二叉排序树的每个节点的有子树要么为空，要么右子树的任意节点的权值v‘一定大于v。

　　　　二叉排序树的节点：每个节点维护如下信息：该点代表的权值，该点的左右儿子，以该点为根的子树含有元素的个数(不等于子树大小。因为两个相同的元素被认为含有两个元素，但是对应的节点只有一个），该点代表的权值的元素的个数。

　　　　二叉排序树的插入：

　　　　　　　对于要插入的值key，比较他与当前节点的权值v关系，如果v>key，则递归插入左子树，

　　　　　　　否则，如果v==key，则插入当前节点，即++该点元素个数。

　　　　　　　否则，递归插入右子树。

　　　　二叉排序树的删除：

　　　　　　　递归过程同上。- - 该点元素个数。

 

Definition

　　　　Treap=tree+heap，直译树堆。在形态上，他是一颗BST，即二叉排序树。同时，由于二叉排序树的插入方式过于朴素，导致给出具有单调性的数据后会被卡成一条链，任何操作的复杂度从期望O(nlogn)上升到O（n2）。为了防止毒瘤出题人造出卡死二叉排序树的数据，我们选择使用魔法打败魔法使用随机化的方法将树的形态按照一定的法则随机转化，防止出现卡出链的情况。

　　　　为了转化树形，我们人为地给每个节点加入一个权值k，强制要求对于每两个有父子关系的节点，父节点的k值小于(大于)子节点。并使用一系列的魔法旋转方式保证树符合这个性质。在旋转的过程中，我们改变了树高，从而改变了整个树的形态。由于父子节点有严格的大小关系，我们说treap具有堆得性质。但是需要指出的是，堆一定是一颗完全二叉树，但treap不满足此性质。

　　　　复杂度：在期望意义下，treap的树高为logn，所以treap的期望时间复杂度为O(nlogn)。

　　　　功能：查询一个序列中第k大的数；通过加入、删除维护该序列；查询序列中一个数x的前驱、后继。

　　　　操作：

　　　　　　1、插入。同二叉排序树。注意每次插入完进行update，同时尝试旋转。

　　　　　　2、旋转。（注：习惯问题，和江湖上流行的左右旋方向恰好相反）通过左旋和右旋，可以将树转化成满足堆性质的BST。以右旋为例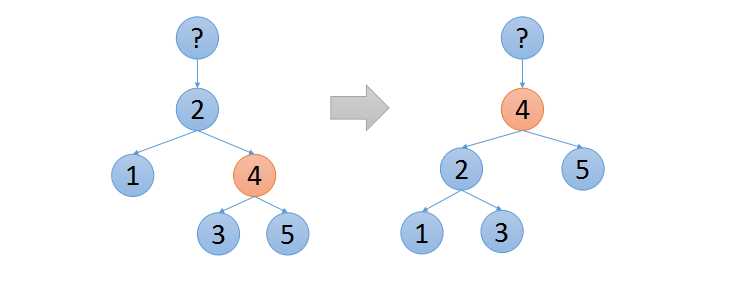：技术分享图片

　　　　　　　　可以看到，右旋时，老根、新根左移。新老根儿子的信息被改变。他们儿子的信息不被改变。

　　　　　　定理：对于每次递归，最多旋转一次。

　　　　　　　　证明：

　　　　　　　　　　由于插入一定会插入到叶节点，在叶节点时显然该子树是一颗合法的树。

　　　　　　　　　　不妨设左右两颗子树均合法，考虑如果出现中间节点不合法的情况，一定是有一侧经过了旋转转换了根。由于不可能同时递归左右两棵子树，所以另一侧的子树一定相对于中间节点合法。在旋转的过程中不难发现合法的一侧其节点相对位置是不变的，即仅交换了不合法的一对的位置，所以只会旋转一次。

　　　　　　　　证毕。

　　　　　　　查询：

　　　　　　　　　　序列第K大：如果左子树的size大于k，则递归左子树

　　　　　　　　　　　　　　　 否则如果左子树的size加上根节点的元素个数大于等于k，则返回当前节点的v

　　　　　　　　　　　　　　　　否则递归查找右子树的k-左子树size-根节点size。

　　　　　　3、删除。　

　　　　　　　　　　删除时，如果该节点对应size>1，则- -size，否则将其权值k赋为INF，通过比较左右子树k的大小决定谁做新的根，经过不断的左右旋转将其沉到叶节点。然后将该节点父节点的指针清空。这样就完成了删除。在数组版的treap中，这么做会产生内存泄漏问题，不过问题不大（逃）如有需要可以手写内存池。

　　　　　　4、前驱、后继。

　　　　　　　　　　一个数x的前驱定义为小于这个数的最大的数。递归整棵树，递归过程如下：

　　　　　　　　　　　　如果当前节点为空，返回—INF。

　　　　　　　　　　　　否则，如果当前节点的v<x 则返回max(v,递归当前节点的右子树)

　　　　　　　　　　　　否则返回当前节点左子树的递归值。

　　　　　　　　　　后继同理。

Sample

【lgP3369】 普通平衡树

Description

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入 x 数
  2. 删除 x 数(若有多个相同的数，因只删除一个)
  3. 查询 x 数的排名(排名定义为比当前数小的数的个数 +1 。若有多个相同的数，因输出最小的排名)
  4. 查询排名为 x 的数
  5. 求 x 的前驱(前驱定义为小于 x ，且最大的数)
  6. 求 x 的后继(后继定义为大于 x ，且最小的数)

Input

第一行为 n ，表示操作的个数,下面 nn 行每行有两个数 opt 和 x ， opt 表示操作的序号( 1≤opt≤6 )

Output

对于操作 3,4,5,63,4,5,6 每行输出一个数，表示对应答案

Sample Input

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

Sample Output

106465
84185
492737

Hint

1.n的数据范围：n≤100000

2.每个数的数据范围：[−107,107]

Solution

模板题。代码拆分如下：

1、定义：

struct BST {
    int v,k,ls,rs,sm,sz,fa;
    BST() {v=-INF;k=INF;ls=rs=fa=-1;sm=sz=0;}
};
BST treap[maxn];int tsz;

其中，v代表键值，k代表权值（即随机给定的值），ls、rs为左右儿子的下标，sm=same即键值为v的元素个数。sz=size为以该节点为根的子树大小。fa♂为父节点。构造函数上，注意初始化sm=sz=0可以保证程序鲁棒。tsz=totalsize，代表当前用到的最大数组下标。

2、声明：

void T_begin();
void lftun(int);
void rtun(int);
void turnning(int);
void rememory(int);
void buildnew(int,int);
void addthis(int);
void dltthis(int);
void build(int,int);
void add(int,int);
void dlt(int,int);
int rak(int,int);
int ask_rak(int,int);
int ask_upper(int,int);
int ask_lower(int,int);

只是给你体验一下他的恐怖

3、初始化

　　添加一个键值超级大权值超级小的点作为超级根，所有的函数都将从超级根开始向下递归。真正的BST是超级根的左子树。

inline void T_begin() {
    treap[0].v=INF;treap[0].k=-INF;treap[0].sz=treap[0].sm=1;
}

4、添加点

核心函数：

void add(int now,int v) {
    BST &t=treap[now];
    if(t.v==-INF) {buildnew(now,v);return;}
    if(t.v==v) {addthis(now);return;}
    if(t.v>v) {
        if(t.ls==-1) t.ls=++tsz,treap[tsz].fa=now;
        add(t.ls,v);
    }
    else {
        if(t.rs==-1) t.rs=++tsz,treap[tsz].fa=now;
        add(t.rs,v);
    }
    turnning(now);
    rememory(now);
}

其中，now代表当前节点的下标，v代表要添加的值。

其中有++size的语句为新开节点存储该元素。

其中buildnew函数如下：

inline void buildnew(int now,int v) {
    BST &t=treap[now];
    t.v=v;t.sm=1;t.sz=1;t.k=rand();
}

addthis函数如下：

inline void addthis(int now) {
    BST &t=treap[now];
    ++t.sm;++t.sz;
}

这两个函数分别对应当前的树上有v对应的节点和没有v对应的节点。

代码中tunning函数如下：

inline void turnning(int now) {
    BST &t=treap[now];
    if((t.ls!=-1)&&(t.k>treap[t.ls].k)) lftun(now);
    else if((t.rs!=-1)&&(t.k>treap[t.rs].k)) rtun(now);
}

　　其中，如果左儿子小，那么右儿子一定合法，进行左旋lftun：

inline void lftun(int now) {
    BST &t=treap[now];
    int f=t.fa,newrt=t.ls;
    t.ls=treap[newrt].rs;if(treap[newrt].rs!=-1) treap[treap[newrt].rs].fa=now;
    t.fa=newrt;treap[newrt].rs=now;
    if(treap[f].ls==now) treap[f].ls=newrt,treap[newrt].fa=f;
    else treap[f].rs=newrt,treap[newrt].fa=f;
    rememory(now);rememory(newrt);
}

　　反之，如果右儿子小，进行右旋rtun：

inline void rtun(int now) {
    BST &t=treap[now];
    int f=t.fa,newrt=t.rs;
    t.rs=treap[newrt].ls;if(treap[newrt].ls!=-1) treap[treap[newrt].ls].fa=now;
    t.fa=newrt;treap[newrt].ls=now;
    if(treap[f].ls==now) treap[f].ls=newrt,treap[newrt].fa=f;
    else treap[f].rs=newrt,treap[newrt].fa=f;
    rememory(now);rememory(newrt);
}

在上面三个函数中出现的的rememory函数相当于江湖上的update：

inline void rememory(int now) {
    BST &t=treap[now];t.sz=t.sm;
    if(t.ls!=-1) t.sz+=treap[t.ls].sz;
    if(t.rs!=-1) t.sz+=treap[t.rs].sz;
}

需要注意的是，不管是否旋转，当前节点都需要rememory。同时，由于旋转以后now成为了新根newrt的子节点，所以需要先rememory(now)，再rememory（newrt）。因为新根的信息需要用到now。

5、删除

void dlt(int now,int v) {
    BST &t=treap[now];
    if(t.v==v) {dltthis(now);return;}
    if(t.v>v) dlt(t.ls,v);
    else dlt(t.rs,v);
    rememory(now);
}

其中dltthis函数如下：

inline void dltthis(int now) {
    BST &t=treap[now];
    if(t.sm!=1) --t.sz,--t.sm;
    else endthis(now);
}

如果当前节点只有一个元素，则将这个节点彻底删除，调用endthis：

void endthis(int now) {
    BST &t=treap[now];
    t.k=INF;
    while((t.ls!=-1)||(t.rs!=-1)) {
        if(t.ls!=-1) {
            if(t.rs!=-1) {
                if(treap[t.ls].k<treap[t.rs].k) lftun(now);
                else rtun(now);
            }
            else lftun(now);
        }
        else rtun(now);
    }
    if(treap[t.fa].ls==now) treap[t.fa].ls=-1;
    else treap[t.fa].rs=-1;
    for(int i=t.fa;i!=-1;i=treap[i].fa) {
        rememory(i);
    }
}

注意由于我们可能修改了从根节点到叶节点的一条链，所以end以后需要整条途径新型rememory。

6、查询第k大

int rak(int now,int k) {
    BST &t=treap[now];
    if(t.v==k) return treap[t.ls].sz+1;
    if(t.v>k) return rak(t.ls,k);
    return rak(t.rs,k)+treap[t.ls].sz+t.sm;
}

7、查询值为k的数的排名

int ask_rak(int now,int k) {
    BST &t=treap[now];
    if(treap[t.ls].sz>=k) return ask_rak(t.ls,k);
    int s=treap[t.ls].sz+t.sm;
    if(s>=k) return t.v;
    return ask_rak(t.rs,k-s);
}

8、查询x的前驱

int ask_upper(int now,int k) {
    if(now==-1) return -INF;
    BST &t=treap[now];
    if(t.v<k) return mmax(t.v,ask_upper(t.rs,k));
    return ask_upper(t.ls,k);
}

9、查询x的后继

int ask_lower(int now,int k) {
    if(now==-1) return INF;
    BST &t=treap[now];
    if(t.v>k) return mmin(t.v,ask_lower(t.ls,k));
    return ask_lower(t.rs,k);
}

Code

#include<cstdio>
#include<cstdlib>
#define maxn 100010
#define INF 20000020

inline void qr(int &x) {
    char ch=getchar(),lst=‘ ‘;
    while(ch>‘9‘||ch<‘0‘) lst=ch,ch=getchar();
    while(ch>=‘0‘&&ch<=‘9‘) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    if(lst==‘-‘) x=-x;
}

template <typename T>
inline T mmax(const T &a,const T &b) {if(a>b) return a;return b;}
template <typename T>
inline T mmin(const T &a,const T &b) {if(a<b) return a;return b;}
template <typename T>
inline T mabs(const T &a) {if(a>=0) return a;return -a;}

template <typename T>
inline void mswap(T &a,T &b) {T temp=a;a=b;b=temp;}

int n,a,b,tsz;

struct BST {
    int v,k,ls,rs,sm,sz,fa;
    BST() {v=-INF;k=INF;ls=rs=fa=-1;sm=sz=0;}
};
BST treap[maxn];

void T_begin();
void lftun(int);
void rtun(int);
void turnning(int);
void rememory(int);
void buildnew(int,int);
void addthis(int);
void dltthis(int);
void build(int,int);
void add(int,int);
void dlt(int,int);
int rak(int,int);
int ask_rak(int,int);
int ask_upper(int,int);
int ask_lower(int,int);

int main() {
    srand(71806291);
    qr(n);
    T_begin();
    while(n--) {
        a=b=0;qr(a);qr(b);
        switch(a) {
            case 1:
                add(0,b);break;
            case 2:
                dlt(0,b);break;
            case 3:
                printf("%d\n",rak(0,b));break;
            case 4:
                printf("%d\n",ask_rak(0,b));break;
            case 5:
                printf("%d\n",ask_upper(0,b));break;
            case 6:
                printf("%d\n",ask_lower(0,b));break;
        }
    }
    return 0;
}

inline void T_begin() {
    treap[0].v=INF;treap[0].k=-INF;treap[0].sz=treap[0].sm=1;
}

inline void buildnew(int now,int v) {
    BST &t=treap[now];
    t.v=v;t.sm=1;t.sz=1;t.k=rand();
}

inline void lftun(int now) {
    BST &t=treap[now];
    int f=t.fa,newrt=t.ls;
    t.ls=treap[newrt].rs;if(treap[newrt].rs!=-1) treap[treap[newrt].rs].fa=now;
    t.fa=newrt;treap[newrt].rs=now;
    if(treap[f].ls==now) treap[f].ls=newrt,treap[newrt].fa=f;
    else treap[f].rs=newrt,treap[newrt].fa=f;
    rememory(now);rememory(newrt);
}

inline void rtun(int now) {
    BST &t=treap[now];
    int f=t.fa,newrt=t.rs;
    t.rs=treap[newrt].ls;if(treap[newrt].ls!=-1) treap[treap[newrt].ls].fa=now;
    t.fa=newrt;treap[newrt].ls=now;
    if(treap[f].ls==now) treap[f].ls=newrt,treap[newrt].fa=f;
    else treap[f].rs=newrt,treap[newrt].fa=f;
    rememory(now);rememory(newrt);
}

inline void turnning(int now) {
    BST &t=treap[now];
    if((t.ls!=-1)&&(t.k>treap[t.ls].k)) lftun(now);
    else if((t.rs!=-1)&&(t.k>treap[t.rs].k)) rtun(now);
}

inline void rememory(int now) {
    BST &t=treap[now];t.sz=t.sm;
    if(t.ls!=-1) t.sz+=treap[t.ls].sz;
    if(t.rs!=-1) t.sz+=treap[t.rs].sz;
}

inline void addthis(int now) {
    BST &t=treap[now];
    ++t.sm;++t.sz;
}

void endthis(int now) {
    BST &t=treap[now];
    t.k=INF;
    while((t.ls!=-1)||(t.rs!=-1)) {
        if(t.ls!=-1) {
            if(t.rs!=-1) {
                if(treap[t.ls].k<treap[t.rs].k) lftun(now);
                else rtun(now);
            }
            else lftun(now);
        }
        else rtun(now);
    }
    if(treap[t.fa].ls==now) treap[t.fa].ls=-1;
    else treap[t.fa].rs=-1;
    for(int i=t.fa;i!=-1;i=treap[i].fa) {
        rememory(i);
    }
}

inline void dltthis(int now) {
    BST &t=treap[now];
    if(t.sm!=1) --t.sz,--t.sm;
    else endthis(now);
}

void add(int now,int v) {
    BST &t=treap[now];
    if(t.v==-INF) {buildnew(now,v);return;}
    if(t.v==v) {addthis(now);return;}
    if(t.v>v) {
        if(t.ls==-1) t.ls=++tsz,treap[tsz].fa=now;
        add(t.ls,v);
    }
    else {
        if(t.rs==-1) t.rs=++tsz,treap[tsz].fa=now;
        add(t.rs,v);
    }
    turnning(now);
    rememory(now);
}

void dlt(int now,int v) {
    BST &t=treap[now];
    if(t.v==v) {dltthis(now);return;}
    if(t.v>v) dlt(t.ls,v);
    else dlt(t.rs,v);
    rememory(now);
}

int rak(int now,int k) {
    BST &t=treap[now];
    if(t.v==k) return treap[t.ls].sz+1;
    if(t.v>k) return rak(t.ls,k);
    return rak(t.rs,k)+treap[t.ls].sz+t.sm;
}

int ask_rak(int now,int k) {
    BST &t=treap[now];
    if(treap[t.ls].sz>=k) return ask_rak(t.ls,k);
    int s=treap[t.ls].sz+t.sm;
    if(s>=k) return t.v;
    return ask_rak(t.rs,k-s);
}

int ask_upper(int now,int k) {
    if(now==-1) return -INF;
    BST &t=treap[now];
    if(t.v<k) return mmax(t.v,ask_upper(t.rs,k));
    return ask_upper(t.ls,k);
}

int ask_lower(int now,int k) {
    if(now==-1) return INF;
    BST &t=treap[now];
    if(t.v>k) return mmin(t.v,ask_lower(t.ls,k));
    return ask_lower(t.rs,k);
}

Summary

　　　　1、这是我第一个完全不借鉴其他人代码学习思想后徒手码出的高级数据结构。代码时间5个半小时，思考实现时间两天。将来会越做越好。这是第一个，但绝不是最后一个。

　　　　2、一共194行……传说中的200行毒瘤代码还是被我奶中了emmmm

【数据结构】【平衡树】Treap

标签：节点   改变   手写   模板   考题   程序   调用   大于   思考   

原文地址：https://www.cnblogs.com/yifusuyi/p/9383962.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！