标签:bsp 分解 技术 直接 ima 重要 视觉 假设 应用
求解递归式对于分冶算法的重要性不言而喻
以下介绍了三种求解递归式的方法
1,代换法:
缺点:代换法主要的缺点在于,对于任何递归式,我们先得去猜其解,对于猜错了同学,如果不幸猜出的结果和正确结果相差太大,虽然可以推导,但是意义不大;
优点:代换法相较于递归树法更为严谨,相较于主定理应用范围更广,主定理只能求解类似于T(n) = aT(n/b)+n/c这种形式的递归式;
下面给出一个递归表达式T(n) = 2T(n/2)+n,求其解;
首先猜一下其解为O(nlgn);那么我们只需要证明T(n)<cnlgn即可
先假设T(n)<cnlgn对于n/2也成立,那么T(n/2)<=c(n/2)lg(n/2)也成立
那么必然的T(n)<=2(c(n/2)(lgn/2))+n-=cnlgn-cnlg2+n<=cnlgn-cn+n
以上表达式,在c>=1时永远成立,得证递归式T(n) = 2T(n/2)+n的解为O(n)
其他递归式的求解方式和上面的大体相似;
2,递归树法
递归树方法利用了将递归式分解为一棵递归树的形式来更加直观的求解递归式;
缺点:递归树方法求解递归式因为丢弃了很多低阶项,所以不够严谨;
优点:递归树方法求解递归式从视觉上更为直观,简单。一般可以先运用递归树求解,然后利用代换法更加严谨得证明用递归树求解的解的数学上的正确性;
下面求T(n) = 2T(n/2)+n的解
首先将上述递归表达式用递归树表达出来,
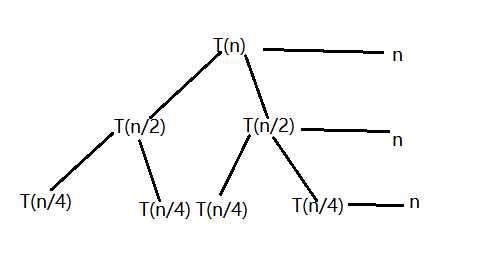
不会画图,比较丑。
以上递归式的深度为lgn,每层的代价为n,自然推导出T(n) = T(n/2)的解为O(nlgn)
以上递归式的求解比较简单更为复杂的求解参考算法导论;
3,主定理
主定理是最为简单求解递归式的解的方法,也是我最为喜欢的一种分析方法
主定理给出如下的如下形式的通用的递归式:T(n) = aT(n/b)+f(n)
主定理套公式分为以下三种情况
符号打得心累直接截图:
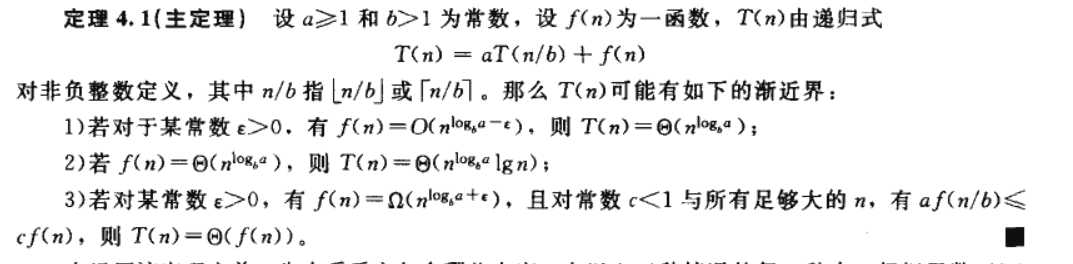
以上为三种递归式的求解方法。
标签:bsp 分解 技术 直接 ima 重要 视觉 假设 应用
原文地址:https://www.cnblogs.com/itqczzz/p/9388214.html