标签:init class get nbsp http log alt span 两种

证明摘自:(我网上唯一看得懂的证明)
https://blog.csdn.net/alan_cty/article/details/54318369
结论:(显然递归实现)
lucas(n,m)=lucas(n/p,m/p)*C(n%p,m%p)
将n,m很大的数压成求两个小于p的组合数的乘积
数学上的卢卡斯定理两种形式:(n,m用p进制表示)
![]()
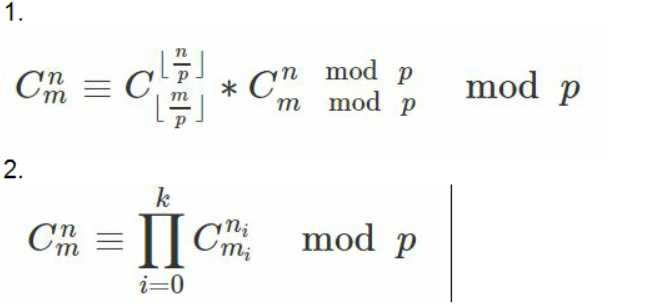



上代码: //打表 void init(ll x){ rec[0]=1; For(i,1,x)mulmod(rec[i],rec[0]*i); } //逆元 ll inv(ll x){ return qmul(x,mod-2); } //求组合数 ll C(ll n,m){ if(n<m)return 0; return rec[n]*inv[rec[m]%mod*inv[n-m]%mod; } //卢卡斯 ll lucas(ll n,m){ if(n<m)return 0; ll ans=1; for(;m;n/=mod,m/=mod) mulmod(ans,C(n%mod,m%mod)); return ans; }
标签:init class get nbsp http log alt span 两种
原文地址:https://www.cnblogs.com/planche/p/9397495.html